Метод Эйлера для решения однородной системы дифф. ур-ий

Согласно методу Эйлера общее решение системы (1) ищется в виде

X=h*e^λ*1 (1)

Где h – вектор – столбец произвольных постоянных (причем, хотя бы один из его элементов должен

λ – число

Значение h и λ необходимо определить в процессе расчета

1. Подставляем решение (1) в систему дифференциального уравнения

dx/dt= A*x

Для этого продифференцируем (1):

d/dt * (h*e^λt)

после подстановки имеем:

λ*h*e^λt=A*h*e^λt

и сокращая на e^λt (не равное нулю) =>

λ*h=A*h

2. Выносим за скобки вектор h, предварительно перенеся все члены в левую часть равенства.

Для вынесения за скобки вектор λh необходимо умножить на Е.

После подстановки решения (1) в систему дифференциальных уравнений получаем:

(λ*E-A)*h=0 (2)

3. Чтобы алгебраическая система (2) имела ненулевое решение, необходимо и достаточно чтобы ее определитель равнялся нулю, (см. решение однородных алгебраических систем) то есть Х являлась корнем уравнения.

det(λ*E-A)=0 (3)

Рассчитывая определитель, получаем уравнение, которое называется характеристическим уравнением:

∆(λ)=λⁿ+b₁*λ^n-1+…+b_n-1*λ+b_n=0 (4)

Корни, полученные при решении уравнения (4) называются характеристическими числами системы, собственным значением матрицы А.

Вектор h называется собственным вектором матрицы А, соответствующего должному λ.

При решении характеристического уравнения (4) возможны случаи получения корней

1. Корни вещественные и различные.

2. Корни вещественные кратные.

3. Корни комплексные.

Порядок решения системы дифференциальных уравнений (хз надо или нет)

1. Записываем матрицу коэффициентов системы дифференциальных уравнений.

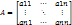
2. Составляем характеристическое уравнение системы.

det(A-λ*E)=0

3. Находим характеристические числа системы (корни характеристического уравнения)

4. В зависимости от вида корней ищем решения системы.