Задания к контрольным работам

На установочной сессии студентам в зависимости от специальности выдается перечень задач, составляющих контрольные работы, в соответст­вии с рабочей программой специальности.

Задача 1

Построить линию пересечения плоскостей, заданных треугольника­ми ABC и EDK, показать видимость. Определить натуральную величину треугольника ABC. Данные для своего варианта взять из табл. 1. При­мер выполнения задачи 1 приведен на рис. 3.

Указания к решению задачи. В левой половине листа формата A3 намечаются оси координат и из табл. 1 согласно своему варианту бе­рутся координаты точек А, В, С, D, Е, К – вершин треугольников. Стороны треугольников и другие вспомогательные прямые проводятся вначале тон­кими сплошными линиями. Линии пересечения треугольников строятся по точкам пересечения сторон одного треугольника с другим или по точкам пересечения каждой из сторон одного треугольника с другим порознь. Та­кую линию можно построить, используя и вспомогательные секущие про­ецирующие плоскости.

Видимость сторон треугольника определяется способом конкури­рующих точек. Видимые отрезки сторон треугольников выделяют сплош­ными основными линиями, невидимые следует показать штриховыми ли­ниями.

Министерство образования и науки Российской Федерации Саратовский государственный технический Университет Кафедра «Начертательная геометрия и компьютерная графика» НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Контрольная работа №____   Выполнил: студент гр._________ Ф.И.О.________________ САРАТОВ 20__ .

Рис. 2. Пример выполнения титульного листа

Таблица 1.

№

XA

YA

ZA

XB

YB

ZB

XC

YC

ZC

XD

YD

ZD

XE

YE

ZE

XK

YK

ZK

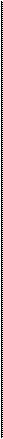
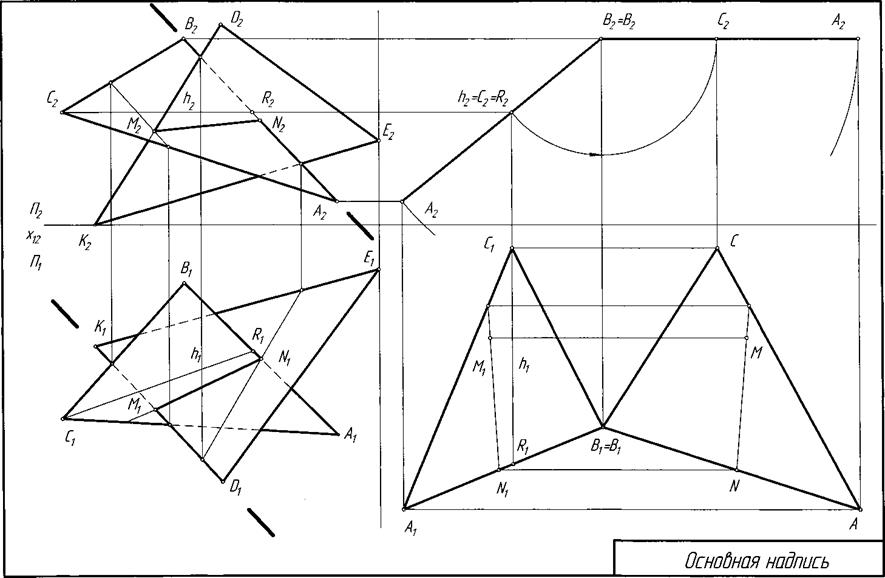
Рис. 3. Пример решения задачи 1.

Определяется натуральная величина треугольника ABC, для чего:

1. В плоскости проводят прямую уровня (горизонталь h ≡ CR).

2. Плоскопараллельным перемещением треугольник ABC

приводится в положение проецирующей плоскости (h₁'^x₁₂), в результате прямая CR становится фронтально-проецирующей прямой, а плоскость ABC - фронтально-проецирующей плоскостью.

3. Вращением вокруг фронтально-проецирующей прямой, проходя­щей через точку В, преобразуем плоскость треугольника ABC в плоскость уровня (горизонтальную, когда он будет параллелен горизонтальной плос­кости проекций).

4. Строится горизонтальная проекция A₁"B₁"C₁", которая является натуральной величиной треугольника.

В треугольнике ABC следует показать и линию MN пересечения его с треугольником EDK.

Все вспомогательные построения должны быть обязательно показа­ны на чертеже в виде тонких линий, а линия пересечения треугольников MN обведена красной пастой.

Задача 2

Построить проекции пирамиды, основанием которой является тре­угольник ABC, а ребро SA определяет высоту h пирамиды. Данные для своего варианта взять из табл. 2. Пример решения задачи приведен на рис. 4.

Указания к решению задачи. В левой половине листа формата A3 намечают оси координат и из табл. 2 согласно своему варианту бе­рут координаты точек А, В и С вершин треугольника ABC. По координа­там строится двухкартинный эпюр треугольника.

В плоскости треугольника ABC проводят линии уровня (горизонталь h и фронталь f). В точке А восстанавливается перпендикуляр к плоскости треугольника, для чего на плоскости П₂ проводят перпендикуляр к фронтали (f₂), на П₁ - к горизонтали (h₁). Для определения натуральной величи­ны ребра SA следует применить способ вращения, который подробно рас­смотрен в пояснениях к решению задачи 5 (рис.7).

На направлении отрезка SA берут произвольную точку S', опреде­ляют натуральную величину отрезка S'A, откладывают заданную высоту пирамиды h и находят проекции вершины пирамиды S (S₁, S₂). Строятся ребра пирамиды.

Способом конкурирующих точек определяется их видимость. Види­мые ребра пирамиды следует показать основными сплошными линиями, невидимые - штриховыми линиями. Все вспомогательные построения не­обходимо сохранить на эпюре и показать их тонкими линиями.

Таблица 2

№	А	В	С	h
x	y	z	x	y	z	x	y	z

Задача 3

Построить линию пересечения пирамиды с прямой призмой. Данные для своего варианта взять из табл. 3. Пример выполнения задачи при­веден на рис. 4.

Указания к решению задачи. В оставшейся правой половине лис­та намечаются оси координат и из табл. 3 согласно своему варианту берутся координаты точек А, В, С и D вершин пирамиды и координаты то­чек E, K, G и U вершин многоугольника нижнего основания призмы. Высота призмы для всех вариантов равна 85 мм. По этим данным строятся проекции многогранников.

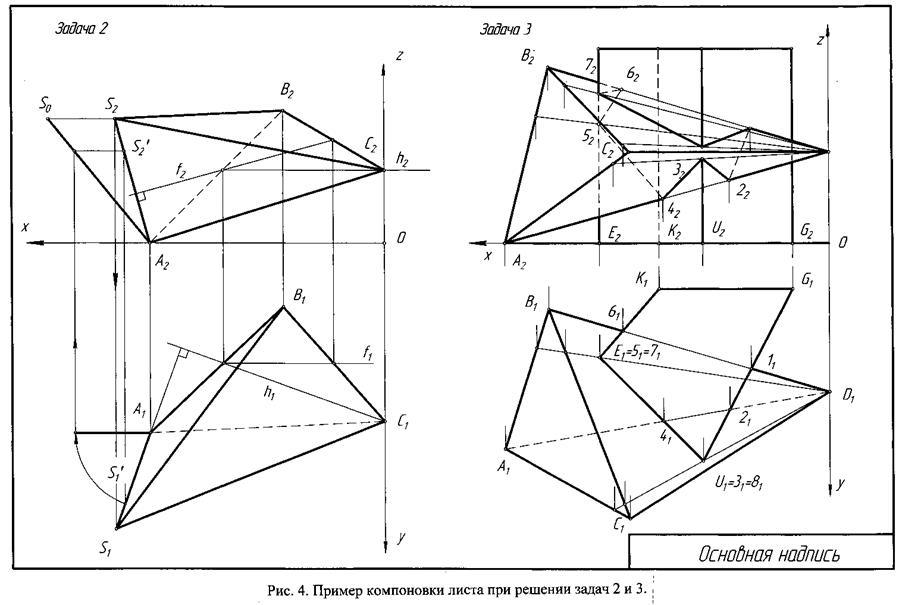
Таблица 3

№

XA

YA

ZA

XB

YB

ZB

XC

YC

ZC

XD

YD

ZD

XE

YE

ZE

XK

YK

ZK

XG

YG

ZG

XU

YU

ZU

Призма своим основанием стоит на плоскости уровня, горизонтальные проекции ее вертикальных ребер преобразуются в точки. Грани боковой поверхности призмы представляют собой отсеки го­ризонтально проецирующих плоскостей.

Линия взаимного пересечения многогранников представляет собой пространственную замкнутую ломаную линию. Для построения линии пересечения сначала находят ее вершины, а затем в определенном порядке соединяют их отрез­ками прямых. Вершины этой линии могут быть определены как точки пе­ресечения ребер одного многогранника (пирамиды) с гранями другого (призмы). Соединяя каждые пары таких точек, принадлежащих одним и тем же граням, от­резками прямых, получаем линию пересечения многогранников.

Видимыми являются только те стороны многоугольника пересече­ния, которые принадлежат видимым граням многогранников. Их следует показать сплошными основными линиями красной пастой. Все вспомога­тельные построения на эпюре сохранить и показать их тонкими линиями.

ПРИМЕЧАНИЕ. Задаче 3 уделить особое внимание. Все построе­ния на чертеже тщательно проверить. Допущенные ошибки приводят к не­правильному решению следующих задач 4, 5 «Построение развертки многогранников».

Задача 4

Построить развертку прямой призмы. Показать на развертке линию пересечения ее с пирамидой. Исходные данные для построений взять из задачи 3. Пример выполнения задачи приведен на рис. 5.

Указания к решению задачи. Разверткой поверхности много­гранника называется плоская фигура, полученная при совмещении с плос­костью чертежа всех его граней, такое совмещение возможно только после предварительных разрезов поверхности по некоторым ребрам.

На листе ватмана формата A3 (297 ĥ 420 мм) строится разверт­ка прямой призмы.

Для построения развертки прямой призмы поступают следующим образом:

а) проводят горизонтальную прямую (при решении задач 3 и 4 на одном листе прямая может являться продолжением оси х);

б) от произвольной точки G этой прямой откладывают отрезки GU,
UE, EK, KG, равные длинам сторон основания призмы;

в) из точек G, U, E, К, G восстанавливают перпендикуляры и на них от­кладывают величины, равные высоте призмы. Полученные точки со­единяют прямой. Прямоугольник GG'G'G является разверткой боковой поверхности призмы. Для указания на развертке граней призмы из точек U, Е, К проводят перпендикуляры;

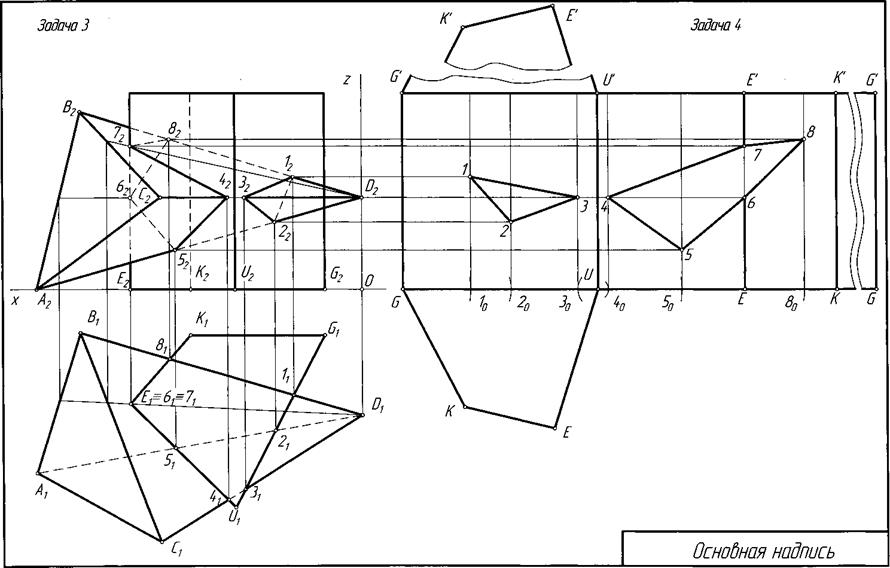
Рис. 5. Пример компоновки листа при решении задач 3 и 4.

г) для получения полной развертки поверхности призмы к развертке боковой поверхности пристраивают многоугольники ее оснований.

Для построения на развертке линии пересечения призмы с пирами­дой замкнутых ломаных линий 1-2-3 и 4-5-6-7-8 пользуемся вертикальными прямыми. Например, для определения положения точки 1 на развертке по­ступаем так: на отрезке GU от точки G вправо откладываем отрезок Gl₀, равный отрезку G₁1₁ (проекция на горизонтальную плоскость) (рис. 5). Из точки 1₀ восстанавливаем перпендикуляр к отрезку GU и на нем отклады­ваем аппликату z точки 1. Аналогично строят и находят остальные точки. Найденные точки соединяют замкнутыми ломаными.

Ребра многогранника на развертке обвести сплошными основными линиями, линии пересечения призмы с пирамидой обвести красной пастой, а все вспомогательные построения выполнить сплошными тонкими ли­ниями.

Задача 5

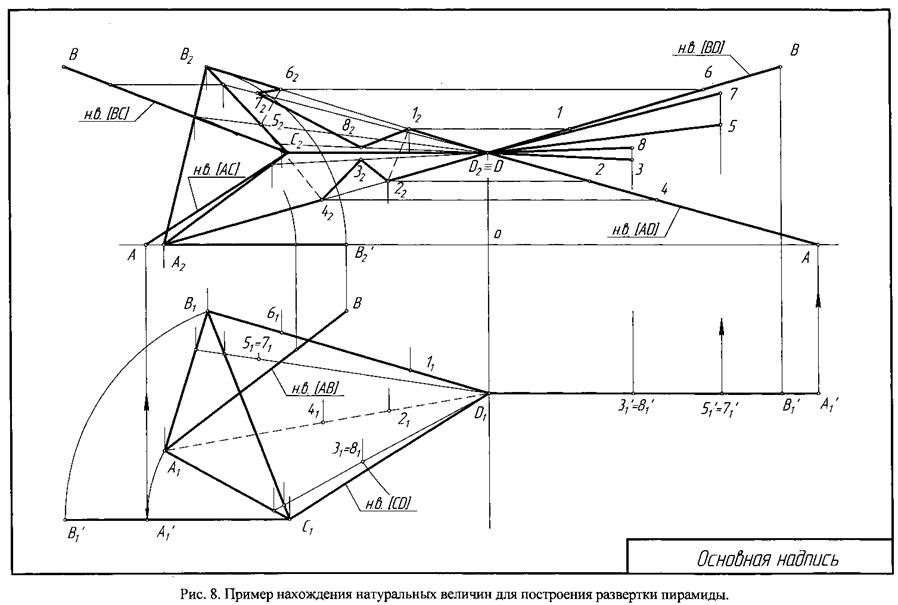
Построить развертку пирамиды. Показать на развертке линию пере­сечения ее с призмой. Исходные данные (призму и пирамиду) для построе­ний взять из задачи 3. Пример выполнения задачи приведен на рис. 8 и 9.

Указания к решению задачи. Развертка трехгранной пирамиды состоит из треугольных граней, каждая из которых строится как тре­угольник по трем заданным сторонам.

Для построения развертки пирамиды необходимо предварительно определить натуральные величины всех ее ребер любым из методов преоб­разования чертежа (способом вращения, способом замены плоскостей проекций или методом прямоугольного треугольника).

На рис. 6 показано построение истинного вида отрезка АВ с помощью прямоугольного треугольника, одним катетом которого служит проекция прямой на одной из плоскостей проекций, а другим - разность расстояний конечных точек отрезка до этой плоскости. На эпюре показана проекция А₁' В₁', которая является натуральной величиной отрезка АВ.

Метод вращения можно рассматривать как частный случай плоскопа­раллельного перемещения, когда все точки пространства и, следовательно, погруженной в него фигуры, перемещаются по дугам окружностей, центры дуг принадлежат одной прямой, называемой осью вращения, а плоскости дуг перпендикулярны к оси. На рис. 7 показано построение истинной величины отрезка АВ вращением вокруг оси, перпендикулярной плоскости П₁. Если повернуть точку А вокруг оси ^ П₁, то ее горизонтальная проекция А₁ по­вернется на такой же угол и займет положение А₁', а ее фронтальная проек­ция будет перемещаться по прямой, перпендикулярной оси вращения. Зная положение горизонтальной проекции А₁', строим фронтальную проекцию А₂' по линии проекционной связи А₁' А₂'. При таком вращении положение точки В остается неизменным, а отрезок АВ приведен к положению линии уровня

(фронтали). Таким образом, преобразованная проекция А₂' В₂' является нату­ральной величиной отрезка АВ.

Определяют последовательно натуральные величины всех ребер пи­рамиды (кроме ребра CD, которое является горизонталью, поэтому его про­екция на плоскость П₁ есть ни что иное как натуральная величина).

На листе ватмана формата A3 (297х 420 мм) строится развертка пирамиды, здесь же выполняются все построения по нахождению натуральных вели­чин ребер пирамиды. На ребрах и гранях пирамиды (на развертке) опре­деляют вершины пространственной ломаной пересечения пирамиды с приз­мой. Последовательно соединяют эти точки, с учетом их принадлежности отдельным граням пирамиды, по описанию в задаче 3.

На рис. 4, 5, 8, 9 приведены варианты размещения задач 3, 4, 5 в зави­симости от содержания контрольных работ для разных специальностей.

Задача 6

На трехпроекционном чертеже построить недостающие проекции сквозного отверстия в сфере заданного радиуса R. Вырожденная (фрон­тальная) проекция сквозного отверстия представлена четырехугольником. Координаты проекций точек А, В, С и D (вершин четырехугольника) заданы в табл. 4. Пример выполнения задачи приведен на рис.10.

Указания к решению задачи. Намечаются оси координат с нача­лом координат в центре листа формата A3. Строятся проекции сферы за­данного радиуса R с центром в точке О. Определяются по заданным ко­ординатам проекции точек А, В, С и D (вершин четырехугольника) сквозно­го отверстия на сфере и строится многоугольник - вырожденная проекция линии сквозного отверстия.

Вначале определяются характерные точки линии сквозного отвер­стия: точки на экваторе, главном меридиане, наиболее удаленные и бли­жайшие точки поверхности сферы к плоскостям проекций. Далее задача сводится к определению недостающих проекций точек поверхности сфе­ры и определению видимости проекции отверстия. Очертание сферы и вы­рожденную проекцию сквозного сечения обвести сплошными основными линиями, невидимые участки поверхности и линии выреза показать линиями невидимого контура (штриховыми). Все вспомогательные построения на чертеже сохранить и обвести тонкими линиями.

Таблица 4

№

О

А

В

С

D

R

x

y

z

x

z

x

z

x

z

x

z

Задача 7

Построить линию пересечения конуса вращения с цилиндром вра­щения. Оси поверхностей вращения - взаимно перпендикулярные проеци­рующие скрещивающиеся прямые. Данные для своего варианта взять из табл. 5.

Указания к решению задачи. Вправой половине листа намечают оси координат и из табл. 5 берут согласно своему варианту величины, которыми задаются поверхности конуса вращения и цилиндра вращения.

Определяют центр (точка К) окружности радиуса R основания кону­са вращения в горизонтальной координатной плоскости. На вертикальной оси на расстоянии h от плоскости уровня и выше ее определяют вершину конуса вращения.

Осью цилиндра вращения является фронтально-проецирующая пря­мая, проходящая через точку Е, основаниями цилиндра - окружности ра­диуса R₁. Образующие цилиндра имеют длину, равную 3 R₁, и делятся по­полам фронтальной меридиональной плоскостью конуса вращения.

С помощью вспомогательных плоскостей определяют точки пересе­чения очерковых образующих одной поверхности с другой и промежуточ­ные точки линии пересечения поверхностей. Проводя вспомогательную секущую фронтальную меридиональную плоскость конуса вращения, оп­ределяют точки пересечения главного меридиана (очерковых образующих) конуса вращения с параллелью (окружностью) проецирующего цилиндра. Выбирая горизонтальную секущую плоскость, проходящую через ось ци­линдра вращения, определяют две точки пересечения очерковых образую­щих цилиндра с поверхностью конуса.

Высшую и низшую, а также промежуточные точки линии пересече­ния поверхности находят с помощью вспомогательных плоскостей уровня (горизонтальных плоскостей). По точкам строят линию пересечения по­верхности конуса вращения с цилиндром вращения и устанавливают ее видимость в проекциях.

Очертания поверхностей вращения следует обвести с учетом види­мости основными сплошными и штриховыми линиями, а линию пересече­ния поверхностей - красной пастой. Все основные вспомогательные по­строения на эпюре сохранить. Их и оси координат показать тонкими сплошными линиями.

Пример решения задачи приведен на рис. 11.

Таблица 5

№	К	R	h	E	R1
x	y	z	x	y	z

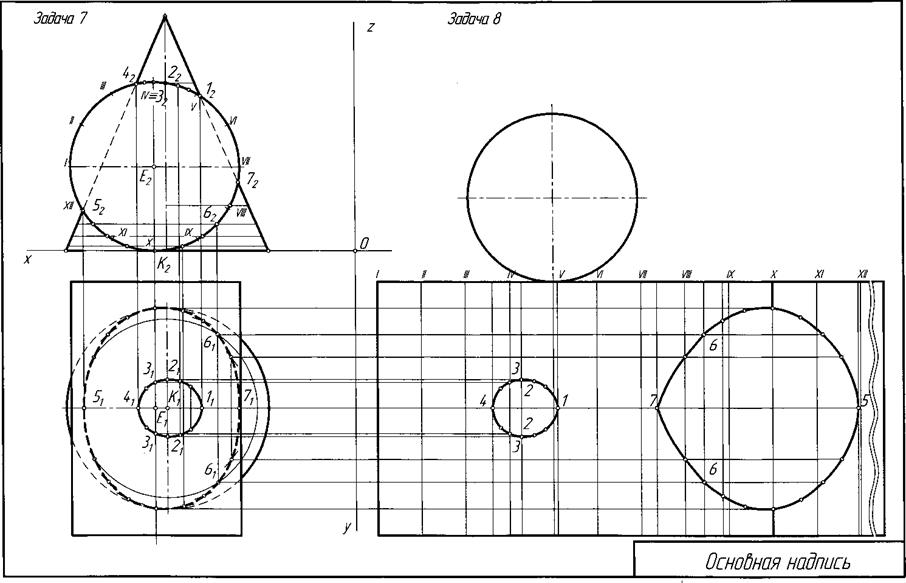
Рис. 11. Пример компоновки листа при решении задач 7 и 8.

Задача 8

Построить развертку цилиндра вращения. Показать на развертке ли­нии пересечения с конусом. В качестве исходных данных использовать результаты решения задачи 7.

Указания к решению задачи. На листе ватмана формата A3 строят развертку поверхности. При решении данной задачи следует пользоваться методом триангуляции (метод построения приближенных разверток развертываемых поверхностей). Он состоит в том, что поверх­ность аппроксимируется многогранной поверхностью, состоящей из жест­ких неизменяемых граней.

Развертка цилиндра вращения.

Развертку цилиндрической поверхности следует выполнять, принимая цилиндр за вписанную в него призму (не менее чем двенадцатигранную). В общем случае выбирают горизонтальную прямую линию и на ней спрямляют линию нормального сечения цилиндра вращения - ок­ружность радиуса R₁ (длина окружности L = 2 ∙ π ∙ R). При решении данной задачи длину окружности приближенно принимают равной спрямленному основанию вписанной в цилиндр прямой призмы. Строят развертку боко­вой поверхности цилиндра. На развертке помечают прямолинейные обра­зующие, проходящие через характерные точки пересечения цилиндра с конусом. Эти точки отмечают на соответствующих образующих. Они оп­ределяют линию пересечения поверхностей развертки. Полная развертка цилиндра вращения представляется разверткой его боковой поверхности и основаниями - окружностями радиуса R₁.

Пример решения задачи приведен на рис. 11.

Задача 9

Построить развертку конуса вращения. Показать на развертке линии пересечения с цилиндром. В качестве исходных данных использовать ре­зультаты решения задачи 7.

Указания к решению задачи. На листе ватмана формата A3 строят развёртку конуса вращения. В общем случае разверткой поверхности конуса вращения является круговой сектор с углом α= R∙360/L, где R - радиус окружности основа­ния конуса вращения; L - длина образующей.

В данном случае развертка конической поверхности должна быть выполнена как развертка вписанной в нее пирамиды (не менее чем двенадцатиграннщй). При необходимости предварительно определяют истинные размеры ребер (образующих) способом вращения или методом прямо­угольного треугольника.

На развертке конуса вращения строят прямолинейные образую­щие или параллели, проходящие через характерные точки линий пересече­ния конуса вращения с цилиндром вращения. Через такие точки прохо­дят линии пересечения поверхностей в преобразовании (на развертке). Контур боковых поверхностей цилиндра и конуса вращения, а также их основания (окружности) обвести основной сплошной линией; линии пе­ресечения заданных поверхностей обвести красной пастой, а все вспомога­тельные построения выполнить основными тонкими линиями.

Пример решения задачи приведен на рис. 12.

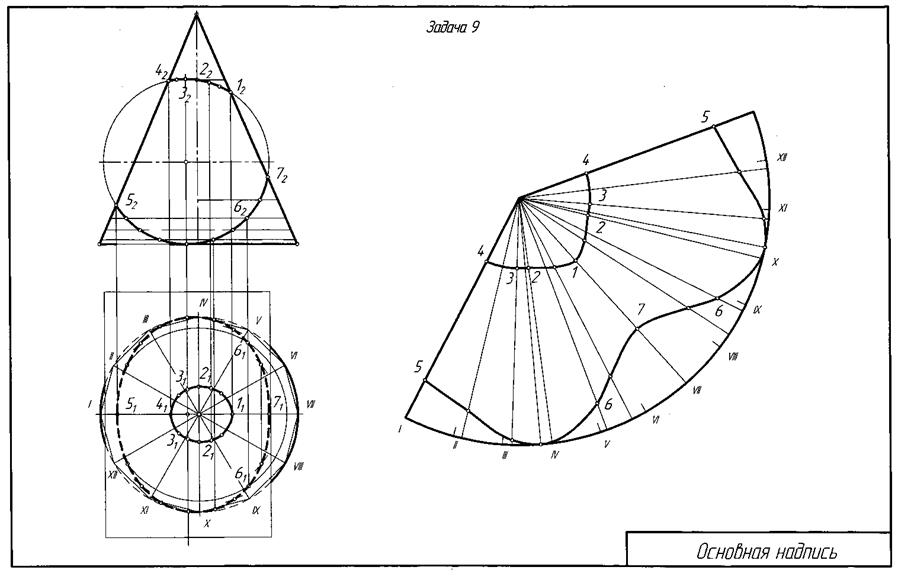
Рис.12. Пример решения задачи 9.

Вопросы для самопроверки

Ктеме 1. Введение. Центральные и параллельные проекции.

1. Какие изображения называют рисунками, какие - чертежами?

2. Какие известны вам основные методы проецирования геометрических форм на плоскости?

3. Сформулируйте основные свойства параллельного проецирования.

4. Что называют обратимостью чертежа?

5. Сформулируйте и покажите на чертежах особенности методов ортого­нальных и аксонометрических проекций.

6. Что называют координатами точки пространства в декартовой системе координат?

7. Укажите основные свойства чертежей геометрических образов.

К теме 2. Точка. Прямая. Плоскость на эпюре Монжа.

1. Постройте трехкартинный эпюр точек, расположенных в различных уг­лах пространства; точек, расположенных в различных октантах.

2. Постройте чертежи отрезков прямых линий, расположенных в различ­ных углах пространства.

3. Укажите частные положения отрезков прямых линий.

4. Какие прямые называют линиями уровня? Проецирующими прямыми?

5. Как изображаются на чертеже пересекающиеся, параллельные и
скрещивающиеся прямые линии?

6. Могут ли скрещивающиеся прямые линии иметь параллельные проекции на плоскостях П) и П₂?

7. Покажите способы задания плоскости общего положения и проецирую­щих плоскостей.

8. Как строят прямые линии и точки в плоскости?

9. Изложите особенности проецирующих плоскостей.

10. Покажите способы построения горизонтали, фронтали и линии наи­
большего наклона плоскостей общего положения и проецирующих плоско­
стей.

К теме 3. Позиционные и метрические задачи.

1. Покажите на примерах, как определяют точки пересечения проецирую­щих плоскостей прямыми линиями, линии пересечения проецирующих плоскостей плоскостями общего положения и проецирующими плоскостя­ми.

2. Изобразите схему и укажите последовательность решения задачи на по­строение точки пересечения прямой с плоскостью общего положения.

3. Как определяют видимость элементов геометрических образов относи­тельно плоскостей проекций?

4. Изобразите схему и укажите последовательность построения линии пе­ресечения двух плоскостей.

5. Изобразите схему и приведите примеры построений прямых линий, па­раллельных и перпендикулярных плоскостям.

6. Сформулируйте условие параллельности и условие перпендикулярности двух плоскостей.

7. Сформулируйте условие перпендикулярности двух прямых общего по­ложения.

8. Как определяются на чертеже расстояния от точки до проецирующей плоскости, плоскости общего положения?

9. Как определяются на чертеже расстояния от точки до прямой частного, общего положения?

К теме 4. Способы преобразования эпюра Монжа.

1. В чем состоит принцип преобразования чертежа способом замены плос­костей проекций?

2. Что определяет направление новой плоскости проекций при переводе плоскости общего положения в проецирующие плоскости?

3. Какова схема решения задачи по определению углов наклона плоскости к плоскостям проекций способом замены плоскостей проекций?

4. Какова схема решения задачи по определению натуральной величины от­сека произвольно расположенной плоскости способом замены плоскостей проекций?

5. В чем состоит принцип преобразования чертежа способом вращения во­круг проецирующих прямых?

6. Какую прямую принимают за ось вращения при переводе отсека плоско­сти из общего положения во фронтально-проецирующую плоскость, в го­ризонтально проецирующую плоскость?

7.Можно ли считать плоскопараллельное перемещение вращением вокруг невыявленных осей (проецирующих прямых) и почему? 8.Укажите последовательность приемов определения натуральной ве­личины отсека плоскости способом плоскопараллельного перемещения. 9. Какова последовательность приемов определения натуральной величины отсека плоскости способом вращения вокруг прямых, параллельных плос­кости проекций?

К теме 5. Многогранники.

1. Какие многогранники называют выпуклыми и выпукловогнутыми?

2. Какие многогранники называют правильными?

3. Назовите правильные выпуклые многогранники.

4. Изложите сущность способов построения линии пересечения многогран­ников.

5. Что называют разверткой многогранной поверхности?

К теме 6. Кривые линии.

1. Какие кривые линии называют алгебраическими?

2. Что называют порядком алгебраической кривой?

3. Что называют кривизной плоской кривой и как ее определяют графиче­ски?

4. Приведите определение эволюты и эвольвенты плоской кривой, назовите основные свойства эволют и эвольвент.

5. Какие кривые называют овалами? Покажите примеры овалов.

6. Какие кривые называют кривыми второго порядка? Расскажите о ка­ждой из них.

7. Какие кривые называют эквидистантными?

8. Как определяют на чертеже направление (ход) цилиндрической винто­вой линии?

9.Расскажите о кривых линиях на сфере.

К теме 7. Поверхности. Образование и задание поверхностей.

1. Каковы основные способы задания поверхностей?

2. Что называют каркасом поверхности?

3. Что называют определителем поверхности?

4. Назовите основные виды перемещений производящей линии.

5. Как образуются и задаются на чертеже поверхности переноса прямоли­нейного направления, поверхности вращения, винтовые поверхности?

6. Какие поверхности вращения называют поверхностями второго порядка?