Метод опорных задач

Суть метода:

Вначале рассматриваются основные задачи, результаты решения или доказательства которых используются для решения других задач.

Опорные задачи:

Задача 1: Докажите, что медиана треугольника меньше полусуммы заключающих его сторон.

Задача 2: Докажите, что в равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.

Задача 3: Биссектриса треугольника является его медианой. Докажите, что треугольник – равнобедренный.

Ключевые задачи:

Задача 1: В треугольнике ABC проведены медианы BD и CE; M — их точка пересечения. Докажите, что треугольник BMC равновелик четырёхугольнику ADME.

Задача 2: Докажите, что в любом неравнобедренном треугольнике биссектриса лежит между медианой и высотой, проведенными из той же вершины.

Задачи для самостоятельного решения:

Задача 1: Точка M лежит внутри треугольника ABC. Докажите, что BM+MC<BA+AC.

Задача 2: Докажите равенство треугольников по стороне и медианам, проведённым к двум другим сторонам.

Задача 3: В треугольнике ABC проведены биссектриса AK, медиана BL и высота CM. Треугольник KLM – равносторонний. Докажите, что треугольник ABC – равносторонний.

Задача 4: Продолжения равных хорд AB и CD окружности соответственно за точки B и C пересекаются в точке P. Докажите, что треугольники APD и BPC равнобедренные.

Задача 5:

а) В треугольнике ABC проведена биссектриса BD внутреннего или внешнего угла. Докажите, что AD:DC = AB:BC.

б) Докажите, что центр O вписанной окружности треугольника ABC делит биссектрису AA₁ в отношении AO:OA₁ = (b + c):a, где a, b, c — длины сторон треугольника.

Решения:

Опорные задачи:

Задача 1: Докажите, что медиана треугольника меньше полусуммы заключающих его сторон.

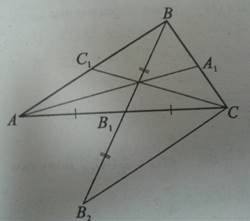
Дано: ∆ABC, BB₁– медиана.

Доказать: BB₁<1/2(BA +BC).

Доказательство:

1. На луче BB₁ от точки B₁ отложим отрезок B₁B₂, равный BB₁.

2. Из ∆BCB₂имеем: BB₂<BC + СB₂.

3. Из равенства треугольников AB₁Bи СB₁B₂ (по двум сторонам и углу между ними) следует равенство сторон ABи B₂C.

Тогда BB₂<BC + BA, но BB₂=2BB₁.Значит, BB₁ < 1/2 (BC + BA).

Аналогично AA₁ < 1/2 (AB + AC); CC₁ < 1/2 (CA + CB).

Задача 2:

Через точку пересечения медиан треугольника ABC проходит прямая, пересекающая стороны AB и AC. Расстояния от вершин B и C до этой прямой равны a и b соответственно. Найдите расстояние от вершины A до этой прямой.

Подсказка

Рассмотрите проекции точек B, A, C и середины стороны BC на данную прямую.

Решение

Пусть M – точка пересечения медиан треугольника ABC; K – середина стороны BC; E, P, Q и F – проекции точек соответственно B, A, K и C на данную прямую. Поскольку AK – медиана треугольника ABC, а M – точка пересечения медиан этого треугольника, то AM:MK = 2:1. KQ – средняя линия прямоугольной трапеции BEFC (или прямоугольника, если b=c). Поэтому

.

Из подобия прямоугольных треугольников KQM и APM следует, что

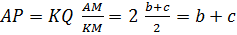
Задача 3:

Биссектриса треугольника является его медианой. Докажите, что треугольник – равнобедренный.

Подсказка

Пусть AM — биссектриса и одновременно медиана треугольника ABC. На продолжении отрезка AM за точку M отложите отрезок MK, равный AM.

Решение

Пусть AM – биссектриса и одновременно медиана треугольника ABC. На продолжении отрезка AM за точку M отложим отрезок MK, равный AM. Треугольник KMC равен треугольнику AMB по двум сторонам и углу между ними. Значит, CK=AB и AKC = BAK, а т.к. AM – биссектриса угла BAC, то AKC = KAC. Поэтому треугольник AKC – равнобедренный. Следовательно, AC=CK = AB, т.е. треугольник ABC – также равнобедренный.

Ключевые задачи:

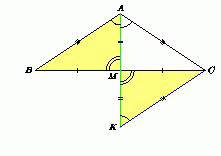
Задача 1:

В треугольнике ABC проведены медианы BD и CE; M — их точка пересечения. Докажите, что треугольник BMC равновелик четырёхугольнику ADME.

Подсказка

Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.

Решение

Проведём медиану AK. Поскольку = 2, то SAMD = SABD = SABC.

Аналогично

SAME = SABC, SCMK = SBMK = SABC.

Следовательно, SADME = SBMC.

Задача 2:

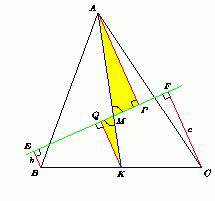
Докажите, что в любом неравнобедренном треугольнике биссектриса лежит между медианой и высотой, проведенными из той же вершины.

Подсказка

Используйте окружность, описанную вокруг треугольника.

Решение

Пусть в треугольнике ABC точки H, D и M - основания соответственно высоты, биссектрисы и медианы, проведенных из вершины B. Опишем около треугольника ABC окружность. Пусть P - точка пересечения прямой BD с этой окружностью. Тогда P - середина дуги AC. Поэтому прямая, проведенная через точку P параллельно BH, перпендикулярна хорде AC и проходит через ее середину, т. е. точку M. Поскольку точки B и P лежат по разные стороны отпрямой AC, то точка D лежит между проекциями концов отрезка BP, т. е. между точками H и M.

Задачи для самостоятельного решения:

Задача 1: Точка M лежит внутри треугольника ABC. Докажите, что BM+MC<BA+AC.

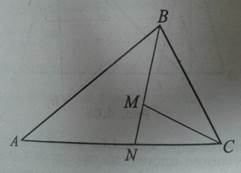
Доказательство:

1. Рассмотрим 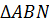, где N = BM∩АС. АВ+АN> 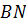(1).

2. Из ∆MNCимеем: MN + NC>MC (2).

3. Сложим равенства (1) и (2).

АВ + АN + MN + N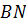C> + MC.

Тогда АВ + АС > 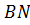- MN + MC и АВ + АС >BM + MC, так как АN + NC = AC и - MN = BM.

Задача 2:

Докажите равенство треугольников по стороне и медианам, проведённым к двум другим сторонам.

Подсказка

Медианы делятся точкой пересечения в отношении 2:1, считая от вершины треугольника.

Решение

Пусть в треугольниках ABC и A₁B₁C₁ равны стороны AC и A₁C₁ и медианы AM = A₁M₁ и CN = C₁N₁. Если O и O₁ — точки пересечения медиан этих треугольников, то

AO = AM = A₁M₁ = A₁O₁, CO = CN = C₁N₁= C₁O₁.

Поэтому треугольники AOC и A₁O₁C₁ равны по трём сторонам. Тогда MAC = M₁A₁C₁ и треугольники AMC и A₁M₁C₁ равны по двум сторонам и углу между ними. Следовательно, треугольники BCA = B₁C₁A₁, BC = 2MC = 2M₁C₁ = B₁C₁.

Аналогично AB = B₁A₁. Поэтому треугольники ABC и A₁B₁C₁ равны по трём сторонам.

Задача 3:

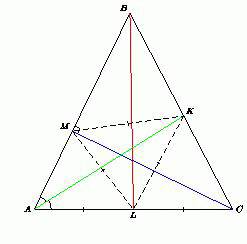
В треугольнике ABC проведены биссектриса AK, медиана BL и высота CM. Треугольник KLM – равносторонний. Докажите, что треугольник ABC – равносторонний.

Решение

Медиана ML прямоугольного треугольника AMC равна половине гипотенузы AC, т.е.

ML=AL=LC.

Поскольку треугольник KLM – равносторонний, KL=LM. Значит, медиана KL треугольника AKC равна половине стороны AC. Поэтому треугольник AKC – прямоугольный, AK KC. Тогда биссектриса AK треугольника ABC является его высотой. Следовательно, треугольник ABC – равнобедренный, AB=AC. Высота AK равнобедренного треугольника ABC является его медианой, значит, K – середина BC. Поэтому MK – медиана прямоугольного треугольника BMC. Тогда

BC= 2MK = 2KL = AC. Следовательно, AB=BC=AC, что и требовалось доказать.

Задача 4:

Продолжения равных хорд AB и CD окружности соответственно за точки B и C пересекаются в точке P. Докажите, что треугольники APD и BPC равнобедренные.

Подсказка

Перпендикуляры OM и ON, опущенные из центра O окружности на равные хорды AB и CD, равны и делят эти хорды пополам.

Решение

Перпендикуляры OM и ON, опущенные из центра O окружности на равные хорды соответственно AB и CD, равны и делят эти хорды пополам, поэтому прямоугольные треугольники POM и PON равны по катету и гипотенузе, значит, PM = PN. Следовательно,

PA = PM + MA = PM + AB = PN + CD = PN + ND = PD,

PB = PA - AB = PD - CD = PC.

Задача 5:

а) В треугольнике ABC проведена биссектриса BD внутреннего или внешнего угла. Докажите, что AD:DC = AB:BC.

б) Докажите, что центр O вписанной окружности треугольника ABC делит биссектрису AA₁ в отношении AO:OA₁ = (b + c):a, где a, b, c — длины сторон треугольника.

Решение

а) Опустим из вершин A и C перпендикуляры AK и CL на прямую BD. Так как CBL = ABK и CDL = KDA, то BLCBKA и CLDAKD. Поэтому AD: DC = AK: CL = AB: BC.

б) Учитывая, что BA₁:A₁C = BA:AC и BA₁ + A₁C = BC, получаем BA₁ = ac/(b + c). Так как BO — биссектриса треугольника ABA₁, то AO:OA₁ = AB:BA₁= (b + c): a.

Список литературы:

1. http://www.problems.ru/view_by_subject_new.php?parent=284&start=10

2. Лисова М.И., Пирютко О.Н. Планиметрия. Итоговое повторение: Пособие для учащихся учреждений, обеспечивающих получение общего среднего образования, −Мн.: Аверсэв, 2004.