Теоретичні відомості. Нехай функція визначена і інтегровна на відрізку

Нехай функція 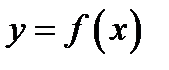визначена і інтегровна на відрізку 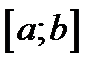. Необхідно знайти значення визначеного інтеграла 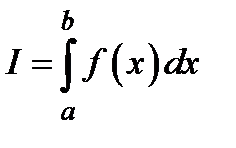, коли першообразна 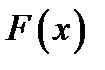, 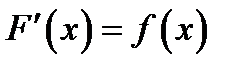невідома або її важко знайти, або 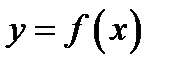задана своїми значеннями , , .

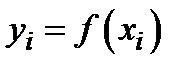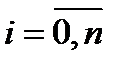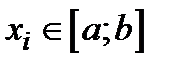Загальний підхід в чисельному інтегруванні полягає в наступному: Для функції 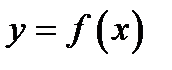будується апроксимуюча функція 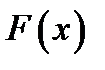, так щоб 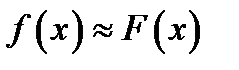на відрізку 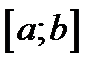, при цьому клас апроксимуючої функції 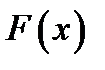може залежати від властивостей функції 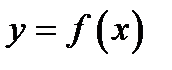, від необхідної точності обчислення інтеграла, від числа арифметичних дій, від часу роботи алгоритму і т.д.;

Функція 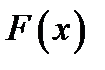вибирається так, щоб інтеграл 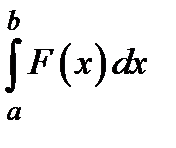легко рахувався;

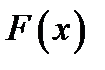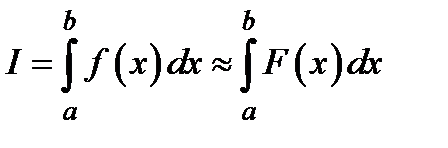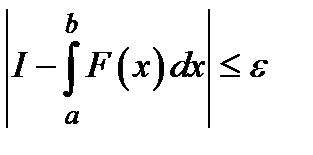a) Функція вибирається так, щоб або , де 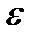- задана точність обчислення інтеграла.

Для застосування методів чисельного інтегрування ділять відрізок 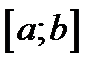системою рівновіддалених точок 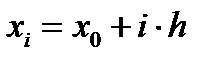, , 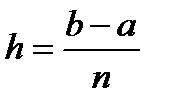, , 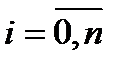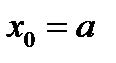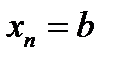на відрізки 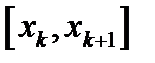, 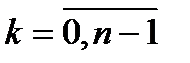і розглядають суму інтегралів .

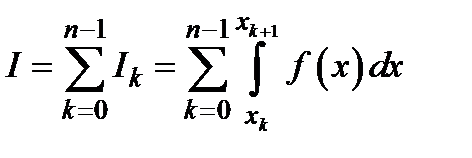Будь – яка прос­­та формула, що ап­прок­си­мує окремий ін­теграл 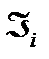, на­зы­­вaеться квад­ра­тур­ною. Составна квад­ра­­тур­ная формула - це фор­му­­­ла, яка дає приближеня ін­­­те­­гра­ла 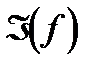у вигляді суми приближень ін­те­­гра­ла­ми 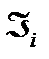по дан­­ій квад­ра­тур­ній формулі.

Виходячи з цих міркувань і припущень зазвичай використовують такі формули чисельного інтегрування.

Формула лівих прямокутників. У цьому випадку 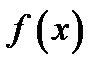на відрізку 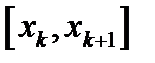замінюється функцією 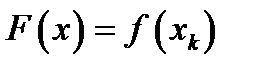, тоді

,

, .

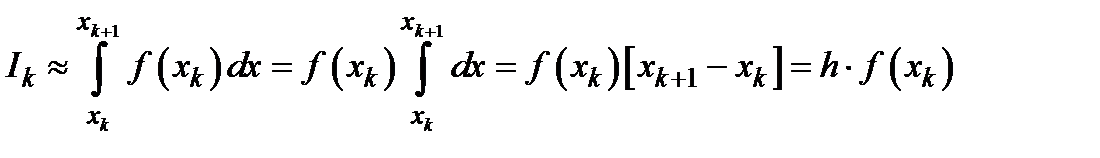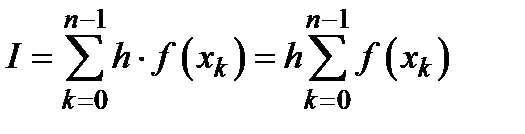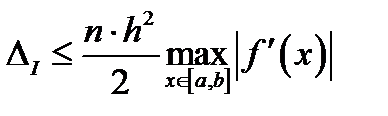1. Формула правих прямокутників. В цьому випадку 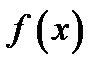на відрізку 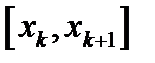замінюється функцією 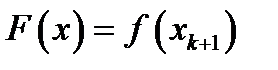, тоді:

,

, .

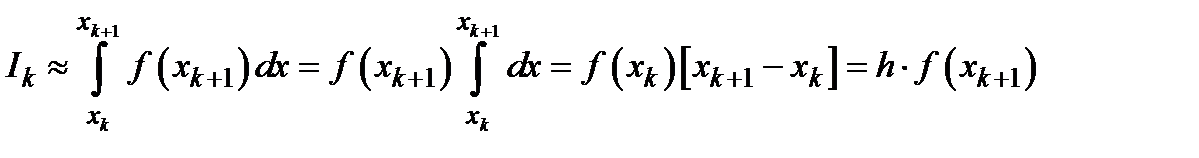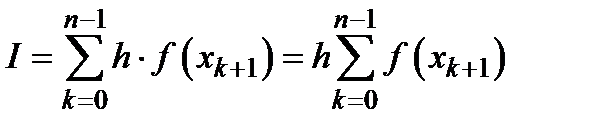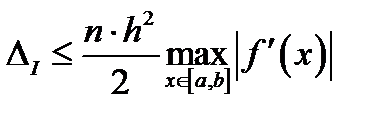2. Формула середніх прямокутників. В цьому випадку 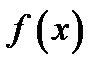на відрізку 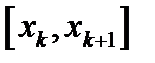замінюється функцією 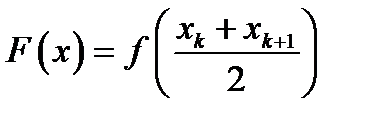, тоді

,

, .

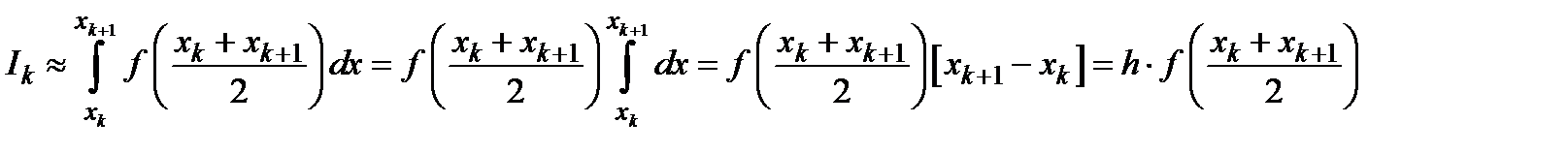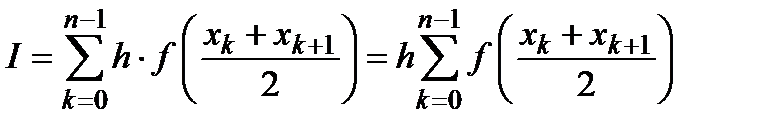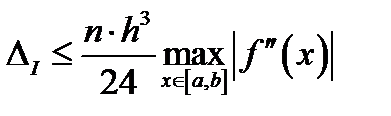3. Формула трапецій. В цьому випадку 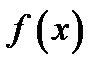на відрізку 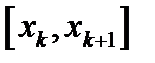замінюється функцією 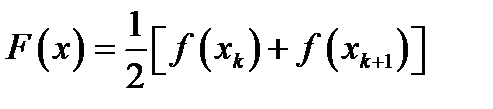, тоді

,

, .

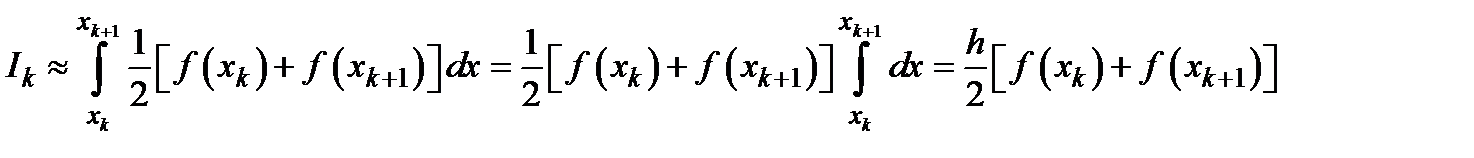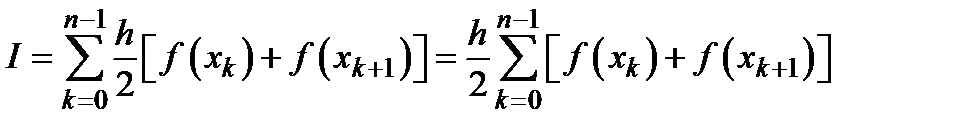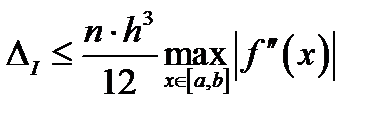4. Формулы Ньютона-Котеса. Якщо 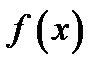на відрізку 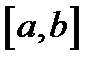замінити інтерполюючим поліномом Лагранжа 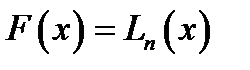, то отримаємо формули Ньютона-Котеса

, , .

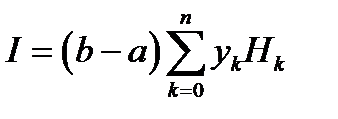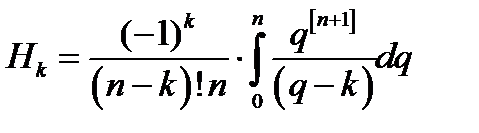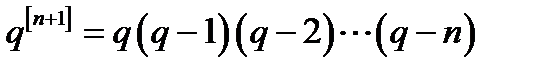Якщо 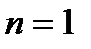отримаємо з цих співвідношень формулу трапеції.

5. Формула Сімпсона. Виходить з формул Ньютона-Котеса при парному числі разбиттів 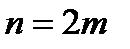відрізку 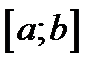та розгляді інтерполяції функції 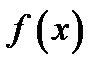на трьох точках, тобто 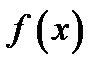приближается квадратичним трьохчленом виду :

, .

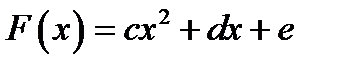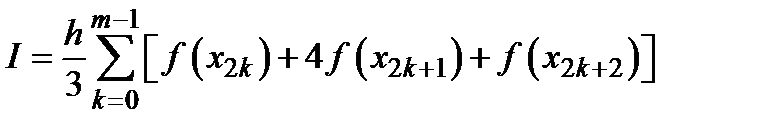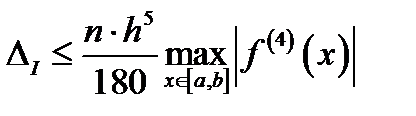6. Гауссоии квадратури - дуже потужний засіб інтегрування, що дозволяє будувати формули на основі N точок, точні для поліномів ступені 2N-1.

Гауссова квадратура визначається для заданих меж інтегрування [a, b], вагової функції W(x) і числа вузлів N. Для кожного такого набору параметрів існує свій набір вузлів x_i и вагів w_i , що визначає квадратурну формулу::

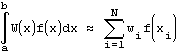
Ця квадратурная формула точна для поліномів ступеня 2N-1 і нижче. Висока точність гауссова квадратур досягається за рахунок спеціального вибору не тільки вагових коефіцієнтів w_i , але ж і вузлів x_i .

Гаусоиы квадратури эфективні тілько для гладких підінтегральних функцій f(x). Тоббто добуток W(x)f(x) може бути негладкою функцією, но f(x) має бути гдадкою, інакше квадратурная формула втратить частину своєї високої точності, інакше квадратурна формула втратить частину своєї высокої точності.

Квадратурна формула Гауса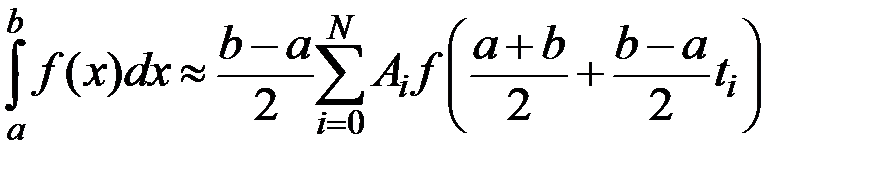

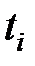- вузли, 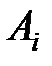- вага.

Таблиця 8.1 – Таблиця вузлів і ваги квадратурної формули Гаусса

Вузли і вага	Число вузлів 1	Число вузлів	Число вузлів	Число вузлів
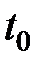
		-0.577350269189626	-0.77459666929954	-0.861136311594052
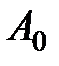
		1.000000000000000	0.55555555555556	0.347854845137454
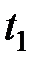
		0.577350269189626	0.00000000000000	-0.339981043584856
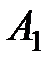
		1.000000000000000	0.88888888888888	0.652145154862546
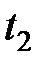
			0.77459666929954	0.339981043584856
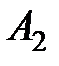
			0.55555555555556	0.652145154862546
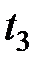
				0.861136311594052
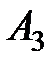
				0.347854845137454

7. Похибка в обчисленні визначених інтегралів за наближеними формулами залежить ввід кроку разбиття інтервалу інтегрування h і від гладкості ін­те­груємої функ­ції f (x), тому в загальному випадку заздалегідь вирахувати похибку інтегрування неможливо. На практиці для оцін­ки похибки ­користуються зручним правилом Рун­ге.

В загальному випадку, коли інтегрується функція деякою квадратурною формулою порядку m, то­гді похибка оцінюється по формулі:

де у виразі в правій частині стоять тільки відомі величини - значення ин­тег­ра­лів, розраховані для кроків h_i і h_i / 2.