Означення випадкового процесу

ЛАБОРАТОРНА РОБОТА № 1

ЗАКОНИ РОЗПОДІЛУ І ОСНОВНІ ХАРАКТЕРИСТИКИ ВИПАДКОВИХ ВЕЛИЧИН

Мета роботи

Дана робота допоможе вивчити закони розподілу і основні характеристики випадкових величин.

Означення випадкового процесу

Поняття випадкового процесу є узагальненням поняття випадкової величини.

Випадковим процесом 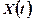називається процес, значення якого при будь-якому фіксованому 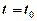є випадковою величиною .

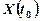Випадкова величина 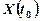.називається розрізом випадкового процесу, якій відповідає даному значенню аргументу .

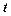Припустимо, що проведено випробування, в ході якого випадковій процес набув повністю визначений вигляд. Це вже звичайна невипадкова функція аргументу 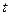. Воно називається реалізацією випадкового процесу 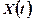в даному випробуванні на проміжку часу .

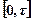Нехай маємо випадковий процес 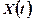. Розріз випадкового процесу 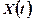для будь-якого 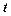є випадковою величиною з законом розподілу

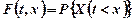. ( 1.1)

Функція (1.1) називається одновимірним законом розподілу випадкового процесу .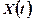

1.3 Числові характеристики випадкового процесу

Математичним сподіванням випадкового процесу 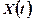називається невипадкова функція 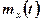, яка для будь-якого 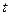дорівнює математичному сподіванню відповідного розрізу випадкового процесу

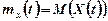. (1.2)

Центрованим випадковим процесом називається процес

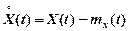. (1.3)

Початковим процесом 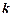-го п орядку випадкового процесу 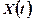називається математичне сподівання 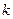-го ступеню відповідного розрізу випадкового процесу:

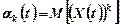. (1.4)

Центральним моментом 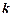-го порядку називається математичне сподівання 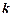-го ступеню центрованого процесу:

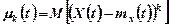. (1.5)

Другий центральній момент називається дисперсією випадкового процесу 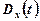, яка для будь-якого 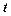дорівнює дисперсії відповідного розрізу випадкового процесу.

Середнім квадратичним відхиленням 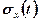випадкового процесу 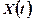називається арифметичне значення кореня квадратного з :

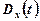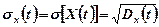. (1.6)

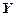Ступінь лінійної залежності між двома випадковими величинами и визначається їх коваріацією

. (1.7)

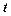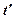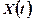Розглянемо два розрізу випадкового процесу для моментів часу і − і 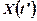. Коваріація дорівнює:

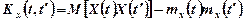. (1.8)

Функція 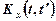називається кореляційною функцією випадкового процесу .

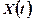Нормованою кореляційною функцією 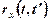випадкового процесу 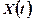називається функція, яка дорівнює

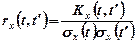. (1.9)

1.4 Деякі розподіли випадкових величин

Розглянемо розподіли дискретних випадкових величин.

1.4.1 Біноміальний розподіл

Нехай проведено 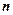− випробувань, в кожному з яких події 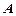відбувається з ймовірністю 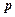. Біноміальним називається розподіл ймовірностей, який визначається формулою Бернулі

, (1.10)

де k = 0, 1, 2, …, n, p − появи події 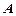в одному випробуванні, .

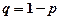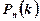− ймовірність того, що подія 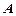з’явиться 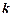разів в 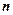випробуваннях.

Закон розподілу можна відобразити у вигляді таблиці:

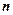
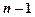
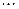
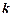
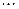
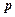
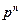
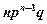
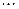
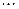
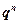
Математичне сподівання біноміального розподілу дорівнює:

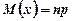. (1.11)

Дисперсія: 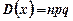. (1.12)

1.4.2 Розподіл Пуассона

Нехай проведено 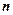− випробувань, в кожному з яких подія 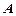відбувається з ймовірністю 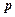( 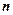велике, 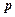мале). Добуток 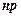зберігає постійне значення 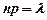. Розподіл ймовірностей, в цьому випадку, називається розподілом Пуассона і виражається формулою

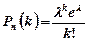. (1.13)

Математичне сподівання розподілу Пуассона дорівнює:

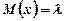. (1.14)

Дисперсія: 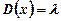. (1.15)

1.4.3 Геометричний розподіл

Нехай проведено 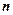− випробувань, в кожному з яких відбувається з ймовірністю 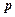, 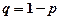. Випробування закінчуються, як тільки з’явиться подія 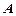. Випадкова величина − кількість випробувань, які потрібно провести до першої появи події 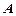. Розподіл ймовірностей визначається формулою:

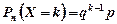, (1.16)

де k = 0, 1, 2, ….

Математичне сподівання геометричного розподілу дорівнює:

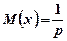. (1.17)

Дисперсія: 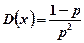. (1.18)

1.5 Неперервні випадкові величини

1.5.1 Нормальний розподіл

Нормальним називається розподіл ймовірностей неперервної випадкової величини, який описується щільністю розподілу:

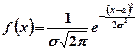. (1.19)

Нормальний розподіл визначається двома параметрами: 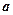− математичне сподівання, 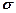− середньоквадратичне відхилення.

1.5.2 Показниковий розподіл

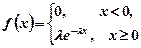, (1.20)

де 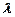− постійна додатна величина.

1.5.3 Рівномірний розподіл

Рівномірнім на відрізку 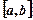називається розподіл ймовірностей неперервної випадкової величини, який описується щільністю розподілу

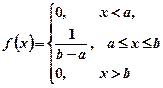, (1.21)

Вариант 19:

Знайти характеристики (математичне сподівання, дисперсію, середньоквадратичне відхилення, кореляційну функцію, нормовану кореляційну функцію) випадкової функції 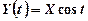, де − дискретна випадкова величина, яка має розподіл за законом Пуассона з параметром .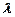

Знайти характеристики (математичне сподівання, дисперсію, середньоквадратичне відхилення, кореляційну функцію, нормовану кореляційну функцію) випадкової функції 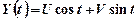, де 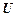− неперервна випадкова величина, яка має показниковий розподіл з параметром 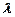, 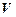− неперервна випадкова величина, яка має рівномірний розподіл на відрізку 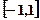, величини 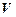і 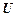− некорельовні.