Алгоритм перебору всіх розбиттів множини

Крок 1. Нехай n = 1. Розбиття множини A = {1} є єдине M₁ = {{1}}. Збільшуємо n на одиницю.

Крок 2. Робимо присвоєння n=n +1. На попередньому кроці ми обчислили усі розбиття M_n-1 множини {1, 2, …, п-1}. Ініціалізуємо розбиття M_n порожньою множиною.

Крок 3. Для кожного з розбиттів множини {1, 2, …, п-1, п} елемент {п} почергово додаємо до кожної з множин розбиття. Отримане розбиття додаємо до M_n. Зауваження: для цього треба організувати подвійний цикл.

Крок 4. Утворюємо розбиття множини {1, 2, …, п-1, п}, додаючи елемент {п} як окрему множину до кожного з розбиттів елементу A та додаємо до M_n.

Крок 5. Переходимо до кроку 2, якщо n не досягло кінцевого значення. ▲

Розглянемо детальніше рекурсивну роботу алгоритму.

Приклад 9.2. Знайдемо розбиття множини M₃.

Крок 1. Нехай n = 1. Розбиття множини A = {1} є єдине – M₁ = {{1}}.

Крок 2. n = 2. Ініціалізуємо M₂ = {}.

Крок 3. Додаємо до M₂ розбиття {{1,2}}.

Крок 4. Додаємо до M₂ розбиття {{1},{2}}.

Крок 5. Ми отримали розбиття M₂ =[{{1,2}};{{1},{2}}] і переходимо до кроку 2.

Крок 6. Ініціалізуємо M₃ = {}. Збільшуємо n на одиницю, n =3.

Крок 7. Додаємо до M₃ розбиття елемент {3}, до кожної з множин розбиттів {{1,2}} та {{1},{2}}.

Отримуємо: M₃ =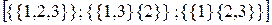

Як бачимо із розбиття {{1},{2}}, ми отримали 2 нових розбиття, а з {{1,2}} – лише одне.

Крок 8. Додаємо до M₃ розбиття, які отримуються від додавання елементу {3}, до кожної з множин розбиття {{1,2}} та {{1},{2}} як окремої множини.

Отримуємо: M₃ =

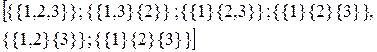
Крок 9. Оскільки n =3, то алгоритм завершено. ▲

Означення 9.1. Кількість усіх розбиттів n -елементної множини на непорожні частини називають числами Белла і позначають S(п).

Означення 9.2. Кількість розбиттів n -елементної множини на k непорожніх частин називають числами Стірлінга другого роду і позначають S (п, k).

З розглянутого прикладу 9.2:

S (3, 1) = 1; S (3, 2) = 3; S (3, 3) = 1; S (3) = 1 + 3 +1 = 5.

Зв’язок між числами Белла та числами Стірлінга очевидний:

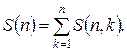
Але для них також виконуються рівності:

;

;

.

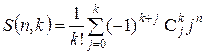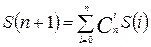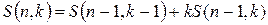Останню рівність легко вивести з алгоритму для генерування множин. Також за її допомогою легко виводити значення чисел Белла та Стірлінга 2-го роду (табл. 9.1).

Таблиця 9.1

n\k							…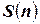
							…
							…
							…
							…
							…
							…
…	…	…	…	…	…	…	…	…

Означення 9.3. Послідовність 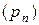дійсних чисел називають унімодальною, якщо існує такий натуральний номер m, що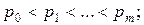 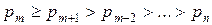, тобто:

· послідовність строго зростає на відрізку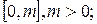

· послідовність строго спадає на відрізку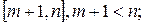

· максимальне значення досягається не більш ніж у двох точках: m і можливо, m+1.

ТЕОРЕМА 9.1. За фіксованого п послідовність 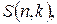k = 1, 2,..., n унімодальна.