Целые занятия

Общей цілью занятие есть научить студентам сознательно использовать теорию вероятности при решении задач медико-биологического профиля.

Конкретные целые занятия:

1. ознакомить студентов с основными идеями, понятиями и методами теории вероятностей, уделяя внимание, главным образом, вопросам, по'язанним с методикой описания закономерностей случайных событий

2. научить студентам вычислять вероятности случайными медицинских событий

3. описывать простые связи между случайными медицинскими величинами, используя теорию вероятности.

Студент должен знать (2 уровень):

1. определение випадковоі события, ее относительную частоту и вероятность.

2. теорему составления вероятностей несовместимых событий

3. теорему составления вероятностей совместных событий

4. теорему умножения вероятностей независимых событий

5. теорему умножения вероятностей зависимых событий

6. теорему полной вероятности

7. теорему Байєса

8. определение случайных величин: дискретной и непрерывной

9. определение распределения, ряд распределения и многокутника распределения дискретной случайной величины

10. определение функции распределения

11. определение мер положения центра распределения

12. определение мер вариабельности значений случайной величины

13. определение щільністі распределения и кривой распределения непрерывной случайной величины

14. определение функциональной залежністі между случайными величинами

15. определение корреляционной залежністі между случайными величинами

16. определение регрессии, уравнение и линии регрессии

17. определение коваріації и коэффициента корреляции

18. определение уравнения линейной регрессии.

Студент должен овладеть элементарными привычками вычисления (3 уровень):

1. вероятностей независимых событий

2. вероятностей зависимых событий

3. мер положения центра распределения

4. мер вариабельности значений случайной величины

5. коваріації и коэффициента корреляции

6. коэффициентов регрессии.

4. Пути реализации целей занятия:

Для реализации целей занятия Вам необходимые такие исходные знания:

1. Определение первоначальной функции

2. Определение неопределенного интегралу

3. Определение определенного интегралу

4. Линейные свойства интеграла.

5. Геометрическое содержание неопределенного интеграла.

6. Определенный интеграл и его геометрическое содержание.

7. Формула Ньютона-Лейбніца.

8. Среднее значение функции.

5. Задача для проверки студентами своего исходного уровня знаний.

1 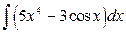. (Правильный ответ )

2 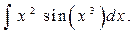(Правильный ответ )

3 . (Правильный ответ )

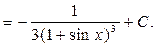4 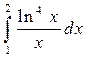. (Правильный ответ .)

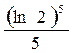5 . (Правильный ответ )

6. Информацию для упрочения исходных знаний-умений можно найти в пособиях:

1 Жуматій П.Г. Сеницька Я.Р. Элементы высшей математики. Методические указания для студентов медицинского інститута. Одесса, 1981.

2 Жуматій П.Г. “ Основы интегрального исчисления”. Одесса, 2009.

3 Жуматій П.Г. “Математическая обработка медико-биологических данных. Задачи и примеры”. Одесса, 2009.

Содержание учебного материала из данной темы с выделением основных узловых вопросов.

Теория вероятностей развивалась как изучения выходов (результатов) испытаний (экспериментов, наблюдений, массовых обследований).

Любой из возможных выходов испытаний называется событием.

Существуют два типа связей между условиями наблюдения и его результатами:

• условия наблюдения однозначно определяют его выход - такие наблюдения называют детерминированными и их результат можно зазделегідь точно предусматривать на основе соответствующих законов;

• при одних и тех же условиях могут происходить виключаючі друг друга события; такие события называют случайными, однако массовое повторение наблюдений при этих условиях дает в среднем результат, который можно предусмотреть с достаточной точностью с помощью статистических закономерностей.

Описанием статистических закономерностей, их изучением и кiлькiсною оценкой занимается теория вероятностей.

Случайное событие массового характера можно охарактеризовать числом, подсчитавши его относительную частоту

,

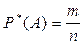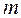- число реализаций случайного события в серии из испытаний.

Более точной характеристикой является вероятность случайного события, которое определяется предельным переходом

.

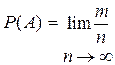Очевидно, что вероятность может принимать значение в интервале

.

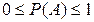Границам этого интервала отвечают:

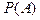• = 0 - событие А никогда не происходит, поэтому такое событие называется невозможной,

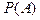• = 1 - событие А происходит всегда, поэтому такое событие называется достоверной.

Реализация любых случайных событий может по-разному влиять на другие случайные события, поэтому различают:

• несовместимые события, когда реализация одних случайных событий исключает наступление других случайных событий,

• совместные события, когда реализация одних случайных событий не исключает наступление других случайных событий.

Зависимые события: событие B называется зависимой от А, если вероятность ее реализации зависит от того, произошло событие А или ни. При этом для зависимого события Во вводится понятия условной вероятности Р (В/А), под которой понимают вероятность реализации события В при условии, что событие А произошла.

Независимые события: события независимые, если Р (В/А) = Р (В), поскольку при этом вероятность реализации события В не зависит от появления А.

Систему несовместимых событий 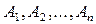называют полной, если при испытании обязательно происходит одна из этих событий.

Понятно, что сумма вероятностей событий, складаючих полную систему, равняется 1, то есть

.

Для кiлькiсного описания результатов испытаний применяют случайные величины, которые принимают значение, которые меняются от испытания до испытания и зависят от тех или других обстоятельств, которые не подвергаются учету.

Различают:

• дискретные случайные величины, которые приобретают лишь отдельные, изолированных значений (число вызовов врача, число случаев заболеваний),

• непрерывные случайные величины, которые приобретают любые значения внутри некоторого интервала (температура тела больного, давка крови).

Случайная величина Х полагает заданной, если известно ее распределение (закон) - соотношение между возможными значениями случайной величины и соответствующими им імовірностями.

Распределение может быть задано в виде таблицы, в виде функции распределения и в виде плотности распределения.

Табличное изображение распределения (его называют также рядом распределения) может быть использовано только для дискретной случайной величины с конечным числом возможных значений 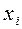(i = 1, 2, 3,..., n):

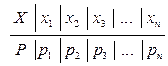
При графическом изображении ряда распределения в прямоугольной системе координат строят точки (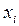, 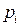) и соединяют их отрезками прямой. Полученную фигуру называют многокутником распределения.

Все возможные значения дискретной случайной величины образовывают полную систему событий, итак,

.

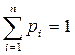Это равенство называют условием нормирования.

Функция распределения 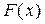является наиболее общей формой изображения закона случайной величины и применяется для задання как дискретных, так и непрерывных случайных величин:

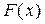= P (X £ x).

Таким образом, функция распределения определяет вероятность того, что случайная величина Х приобретет любое из своих значений, которые не превосходят некоторого числа х.

Графиком функции распределения дискретной случайной величины есть разрывная ступенчатая ломанная линия, а непрерывной случайной величины - плавная непрерывная линия.

Во многих случаях ограничиваются числовыми характеристиками случайной величины. К ним принадлежат:

Меры положения центра распределения:

• математическое ожидание m

,

что характеризует "средний" результат при большом числе испытаний,

• медиана 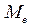- значение случайной величины, для которого функция распределения равняется 0.5, то есть F () = 0.5,

• мода 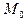- значение дискретной случайной величины, которая имеет самую большую вероятность.

2. Меры вариабельности значений случайной величины:

• дисперсия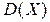

,

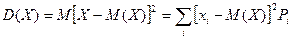• стандартное отклонение

,

• коэффициент вариации C.V.

,

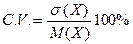что показывают на сколько в среднем случайная величина может отличаться от своего математического ожидания.

Непрервну случайную величину задают функцией плотности распределения вероятностей 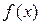, который равняется первой производной от функции распределения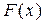

.

График функции плотности распределения вероятностей называют кривой распределения. Значение непрерывной случайной величины, при которому кривая распределения имеет максимум, носит название модой 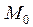непрерывной случайной величины. Поскольку кривая может иметь не один максимум, то согласно них числом бывают двомодальні и многомодальні распределения.

Условие нормирования непрерывной случайной величины выражается формулой

.

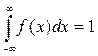Отметим, что функция распределения 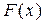выражается через 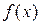с помощью интеграла

.

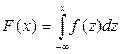Нужно иметь в виду, что размерность функции плотности распределения вероятностей 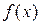зворотня размерности случайной величины х, а функция распределения 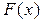, как всякая вероятность, безразмерная величина.

Математическое ожидание и дисперсия непрерывной случайной величины вычисляют за формулами

,

.

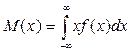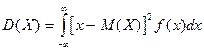Любые две или больше случайные величины, которые изучаются вместе, создают систему. Система может составляться с независимых или зависимых одна от одной случайных величин.

Если каждому значению одной величины X по определенному правилу относится в соответствие значения второй величины Y, то, как известно, зависимость между ними называется функциональной.

При этом, если одна из величин случайная, то и другая, залежачая от нее, также есть случайной. Очевидно, что зависимая случайная величина принимает определенное значение при определенном значении второй только тогда, когда на нее никакие другие случайные факторы не влияют. Таким образом, функционально связанные случайные величины X и Y могут принимать разные значения, но, если X получает любое определенное значение, то ему будет отвечать определенное значение Y.

Если случайная величина Y зависит не только от X, но и от других случайных факторов, то зависимость Y от X уже есть не функциональной, а, как ее называют, корреляционной или стохастичною:

корреляционно связанные случайные величины меняют свои распределения при зміненні значений любой с них.

Другими словами, кожному значению любой из случайных величин, связанных корреляционной зависимостью, отвечает определенное распределение второй случайной величины с новыми значениями числовых характеристик математического ожидания и дисперсии.

Понятие о корреляционной зависимости распространяется также и на якiсні показатели, при условии, которое наличия одного из них отвечает определенная вероятность наличия другого.

Например, содержимое любого гормона в крови зависит от большой кiлькості случайных факторов, поэтому зависимость этой случайной величины от любого с них есть корреляционной.

Для описания корреляционной зависимости применяют функции регрессии, которые определяют математическое ожидание одной из случайных величин для каждого значения второй случайной величины.

Соответствующие формулы называют:

• уравнение регрессии Y на X

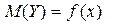
• уравнение регрессии X на Y

.

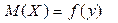Функция регрессии зображається графически линией регрессии. Если обе функции регрессии линейные, то линии регрессии являются прямыми и корреляционная зависимость называется линейной.

Стохастична залежность может быть более-меньш тесной. Степень связи между случайными величинами характеризуют:

• коваріація (корреляционный момент)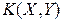

• коэффициент корреляции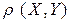

.

Коэффициент корреляции принимает значение в пределах

.

Необходимо помнить, что при

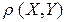• =0 - линейная корреляционная зависимость между случайными величинами X и Y отсутствующая, но это еще не затем, что они вообще не зависят одна от одной (возможная нелинейная корреляционная зависимость); прямые регресій параллельные осям координат и перпендикулярные друг другу.

• >0 - с ростом X случайная величина Y увеличивается.

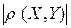• =1 - случайные величины X и Y связаны функциональной зависимостью; прямые регрессії сливаются в единственный график.

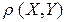• < 0 - с ростом X случайная величина Y уменьшается.

С коэффициентом корреляции 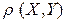связанные:

• коэффициент регрессии Y на X

,

• коэффициент регрессии X на Y

.

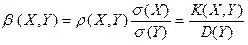С помощью этих коэффициентов записывают:

• уравнение линейной регрессии Y на X

,

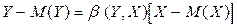• уравнение линейной регрессии X на Y

.

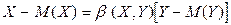• Коэффициент корреляции связан с 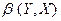и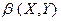

.

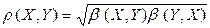Задача для самостоятельной подготовки студентов.

8.1 Задача для самостоятельного изучения материала с темы.

8.1.1.Практическое вычисление вероятностей случайных событий

В ряде случаев высчитать вероятность события оказывается проще, если представить ее в виде комбiнацiї более простых событий и использовать соответствующие теоремы теории вероятностей.

1. Теоремы составления вероятностей

• несовместимые события:

,

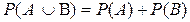где - вероятность появления события А или В (любой);

• совместные события:

,

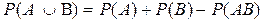где 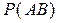- вероятность появления сложного события, которое составляется из реализаций событий А и В.

Пример 1.

Студенту предложен тест, в котором необходимо выбрать единый правильный ответ из 5 вариантов.

Определить вероятность правильного выбора ответа неподготовленным студентом.

Решение. Все 5 вариантов ответов создают полную систему событий, для которой сумма вероятностей равняется 1. Для неподготовленного студента каждый из возможных вариантов выбора одинаково вероятный, поэтому вероятность правильного ответа в этом случае равняется 20%.

Пример 2.

Определить вероятность правильного выбора ответа неподготовленным студентом, если с 5 возможных вариантов 2 верные.

Решение. Для неподготовленного студента каждый из возможных вариантов выбора одинаково вероятный (20%) и несовместимый с другими, поскольку сразу после первого ответа компьютер переходит к следующему вопросу. Поскольку с 5 возможных вариантов 2 верные, а какой cаме с этих 2 правильных ответов студент выберет не имеет значения, то нужно применить теорему составления вероятностей несовместимых событий:

.

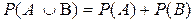Вероятность правильного ответа в этом случае равняется 40%.

Пример 3.

Пусть вероятности двух некоторых заболеваний А и В равняются соответственно 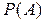= 0,15 и 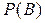= 0,05 и, больше того, возможное наличие обеих заболеваний в одной и той же человека с вероятностью = 0,1.

Определить вероятность того, что в больного одна из этих болезней (безразлично, которая cаме).

Решение. Поскольку в одной и той же человека возможное наличие обеих заболеваний (события А и В совместные), а которая cаме из этих болезней в пациента на данном этапе обследования безразлично, то искомую вероятность нужно вычислять, употребляя теорему составления вероятностей совместных событий:

.

Таким образом, искомая вероятность равняется 0,1.

2. Теорема умножения вероятностей

• независимые события:

,

где 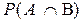- вероятность сложного события, которое составляется из совместного появления событий А и В,

• зависимые события:

,

где 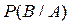- условная вероятность реализации события В при условии, что событие А произошла.

Пример 4.

В отделении 4 пылать. Вероятность того, что на протяжении ночи будет нужна кислородная подушка, для 1-ої и 3-ої палат составляет 0,2, для 2-ої - 0,3, для 4-ої - 0,1.

Определить вероятность того, что на протяжении ночи будет нужна кислородная подушка в 1-в и 4- у палаты.

Решение. Нужды в кислородной подушке для больных в разных палатах не зависят одна от одной, поэтому нужно в данном случае воспользоваться теоремой умножения вероятностей для независимых событий:

.

Искомая вероятность равняется 0,02.

Пример 5.

Пусть вероятность излечения некоторого заболевания при своевременном обращении к врачу равняется 0,7, а вероятность своевременного обращения к врачу равняется 0,5.

Какая вероятность успешного выхода лечения при этих условиях?

Решение. Успех лечения зависит от своевременного обращения к врачу, то есть события зависимые, а затем надо применять теорему умножения вероятностей зависимых событий:

.

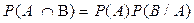В данном случае - условная вероятность реализации события В (успешное лечение заболевание) при условии, что событие А (своевременное обращение к врачу) произошла, равняется 0,7. Подставляя числовые данные, получаем искомый ответ 0,35.

3. Теорема о полной вероятности

,

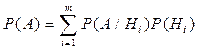где - вероятности событий , которые создают полную систему, 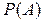- вероятность события А, которое в зависимости от того, которая из событий произошла, реализуется с условными вероятностями .

Пример 6.

В условиях приклада 4 дополнительно известно, что после использования кислородной подушки приходится применять инъекции, при этом соответствующие вероятности для 1-ої и 4-ої палат равняются 0,2, для 2-ої 0,3, для 3-ої 0,1.

Определить вероятность применения инъекций в отделении на протяжении ночи.

Решение. По условию полная система событий (использование кислородной подушки в i - палате) составляется с 4 событий (4 пылать в отделении, то есть m = 4), 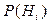- вероятности этих событий, а - условные вероятности применения инъекций в соответствующих палатах после использования кислородной подушки. Для определения вероятности применения инъекций во всем отделении на протяжении ночи нужна теорема о полной вероятности

.

Подставляя числовые данные, находим ответ

= 0,2*0,2+0,3*0,3+0,2*0,1+0,1*0,2 = 0,17.

4. Теорема Байєса

.

где - вероятности событий 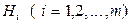, которые создают полную систему, 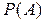- вероятность события А, которая в зависимости от того, которая из событий произошла, реализуется с условными вероятностями 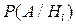, а - условные вероятности событий системы 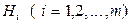, когда событие А уже произошло.

Пример 7.

(Сохраненные условия примера 6). Утром заведующему отделением стало известно, что ночью применялись инъекции. Какая вероятность того, что это произошло в 2-ій палате?

Решение. Известные - вероятности использования кислородной подушки, 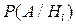- условные вероятности применения инъекций в соответствующих палатах после использования кислородной подушки и известная вирахована в примере 6 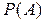- вероятность применения инъекций во всем отделении. Для определения условной вероятности - нужно воспользоваться теоремой Байєса

.

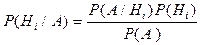Подставляя числовые данные, получаем искомый ответ

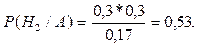
Итак, инъекции использовались в 2-ій палате с вероятностью 53%.