Условие сходимости положительного ряда

Основные понятия теории числовых рядов.

Определение 1. Пусть задана некоторая бесконечная последовательность чисел

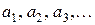(1)

Составленный из этих чисел символ

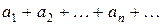(2)

называется бесконечным рядом, а сами числа (1) – членами ряда.

Вместо (2), пользуясь знаком суммы, часто пишут так:

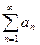; (2а)

показатель 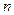пробегает здесь все значения от 1 до 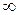. Нумерацию членов ряда иногда начинают не с единицы, а с нуля или же с какого-либо натурального числа, большего единицы.

Станем последовательно складывать члены ряда, составляя суммы

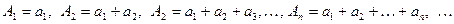(3)

Определение 2. 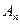называют 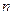-ой частичной суммой ряда (2). Конечный или бесконечный предел 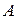последовательности частичных сумм 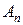называют суммой ряда (2) и пишут

,

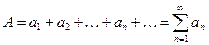придавая тем самым символу (2) или (2а) числовой смысл. Если ряд имеет конечную сумму, то его называют сходящимся, в противном же случае (т.е. если сумма равна 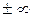, либо же суммы вовсе нет) – расходящимся.

Пример 1. Простейшим примером бесконечного ряда является геометрическая прогрессия:

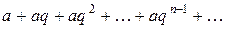
При 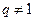имеем 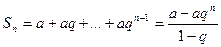. Если знаменатель прогрессии 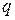будет по абсолютной величине меньше 1, то последовательность 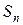имеет конечный предел 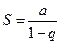, т.е. геометрическая прогрессия в этом случае сходится и ее сумма равна .

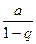При 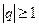та же прогрессия дает пример расходящегося ряда. Действительно, если 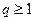, то прогрессия имеет сумму, равную 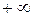или 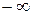, в зависимости от того, будет ли 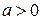или меньше нуля. В том случае, когда 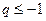, суммы нет вовсе.

2) Ряд 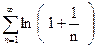расходится, но имеет сумму, равную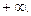

2) Основные теоремы теории числовых рядов.

Определение 1. Если в ряде

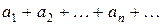(1)

отбросить первые 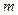членов, то получится ряд

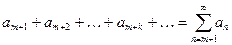, (2)

называемый остатком ряда (1) после 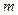–го члена.

Теорема 1. Если сходится ряд (1), то сходится и любой из его остатков (2); обратно, из сходимости остатка (2) вытекает сходимость исходного ряда (1).

Из этой теоремы следует, что отбрасывание конечного числа начальных членов ряда или присоединение в начале нескольких новых членов не отражается на поведении ряда

(в смысле сходимости или расходимости).

Сумму ряда (2), если он сходится, обозначим через 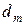, указывая значком 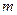, после какого члена берется остаток.

Теорема 2. Если ряд (1) сходится, то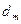

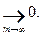
Теорема 3. Если члены сходящегося ряда (1) умножить на один и то же множитель 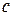, то его сходимость не нарушится (а сумма лишь умножится на ).

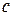Теорема 4. Два сходящихся ряда 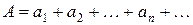и 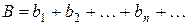можно почленно складывать (или вычитать), так что ряд 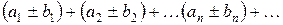также сходится, и его сумма равна, соответственно, .

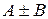Теорема 5(необходимое условие сходимости числовых рядов). Общий член 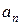сходящегося ряда стремится к нулю.

Замечание1. Общий член расходящегося ряда 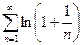стремится к нулю. Таким образом, стремление общего члена к нулю есть условие необходимое, но не достаточное.

Условие сходимости положительного ряда.

Определение1. Ряд, члены которого неотрицательны, называют положительным.

Пусть ряд

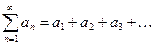
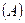
будет положительным. Тогда последовательность 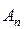его частичных сумм оказывается неубывающей. Вспоминая теорему о пределе монотонной последовательности, мы приходим к следующей основной в теории положительных рядов теореме.

Теорема 1. Положительный ряд 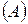всегда имеет сумму; эта сумма будет конечной (и, следовательно, ряд – сходящимся), если частичные суммы ряда ограничены сверху и бесконечной (а ряд – расходящимся) в противном случае.