Понятие дифференцируемости функции в данной точке

Пусть функция 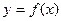определена на некотором интервале 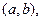и пусть

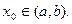Придадим приращение 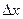, так что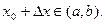

Определение1. Приращением функции 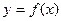в точке , соответствующим приращению аргумента 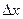, назовем число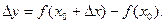

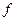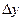Определение 2. Функция называется дифференцируемой в точке , если приращение этой функции в точке представимо в виде

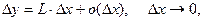(1)

где 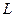– некоторое действительное число.

Теорема 1. Для того, чтобы функция 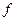была дифференцируема в точке , необходимо и достаточно, чтобы у нее в точке существовала производная. При этом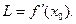

Следствие 1. Если функция f дифференцируема в точке , то она в точке непрерывна.

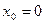Обратное неверно. Так, например, функция непрерывна в точке , но не дифференцируема в этой точке.

Определение 3. Дифференциалом (или первым дифференциалом) функции 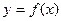в точке (дифференцируемой в этой точке) называется функция аргумента :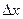

.

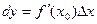Дифференциалом независимой переменной называется приращение этой переменной: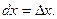

Следовательно,

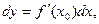(2)

т.е. производная функции 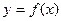в точке равна отношению дифференциала функции в этой точке к дифференциалу независимой переменной.