 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Сравнение бесконечно малых функций
|
|
Определение1. Функция 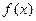 называется бесконечно малой при
называется бесконечно малой при 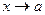 , если
, если 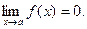
Определение 2. Пусть 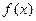 и
и 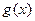 – две бесконечно малые при
– две бесконечно малые при 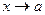 . Функции
. Функции 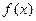 и
и 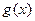 называются:
называются: 
a) бесконечно малыми одного порядка при 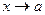 , если
, если 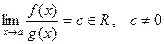 ;
;
b) эквивалентными бесконечно малыми при 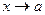 , если
, если 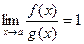 .
.
В первом случае пишут  при
при 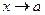 , во втором –
, во втором – 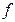 ~
~ 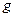 при
при 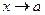 .
.
Если 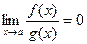 ,
,  то говорят, что
то говорят, что 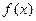 есть бесконечно малая более высокого порядка при
есть бесконечно малая более высокого порядка при 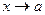 , чем
, чем 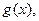 и пишут
и пишут 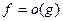 при
при 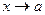 .
.
Пример1. 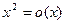 при
при 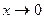 , а
, а 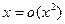 при
при 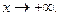
Пример2. 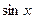 ~
~ 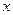 при
при 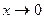 , а
, а 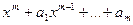 ~
~ 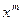 при
при 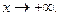
Теорема 1(Свойства эквивалентных функций).
1) Если 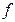 ~
~ 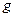 при
при 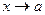 , то для любой функции
, то для любой функции 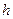 из существования одного из пределов
из существования одного из пределов

вытекает существование второго и их равенство;
2) Если 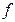 ~
~ 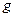 при
при 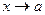 , то для любой функции
, то для любой функции 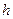 из существования одного из пределов
из существования одного из пределов

вытекает существование второго и их равенство;
3) Если 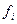 ~
~ 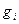 при
при 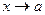 ,
, 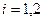 , то
, то
 ~
~ 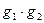 ,
, 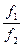 ~
~ 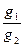 при
при 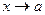 .
.
Заметим, что из того, что 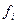 ~
~ 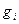 при
при 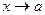 ,
,  , не следует, что
, не следует, что 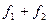 ~
~ 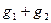 при
при 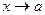 . Действительно,
. Действительно, 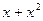 ~
~ 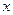 при
при 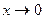 ,
, 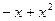 ~
~ 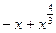 при
при 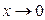 , а
, а 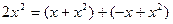 эквивалентным
эквивалентным 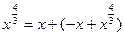 при
при 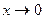 уже не будут.
уже не будут.
Определение3. Функция 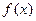 называется бесконечно большой при
называется бесконечно большой при 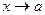 , если
, если 
Пример3. Положим 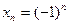 . Очевидно последовательность
. Очевидно последовательность 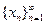 бесконечно большая, но при этом предела у нее нет.
бесконечно большая, но при этом предела у нее нет.
Теорема 3. Если 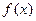 - бесконечно большая при
- бесконечно большая при 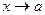 , то
, то 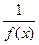 есть бесконечно малая при
есть бесконечно малая при 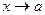 . Обратно, если
. Обратно, если 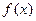 - бесконечно малая при
- бесконечно малая при 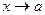 и
и 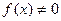
для всех 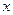 достаточно близких к
достаточно близких к 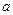 и отличных от
и отличных от 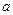 , то
, то 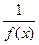 есть бесконечно большая при
есть бесконечно большая при 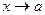 .
.
Дата публикования: 2015-09-18; Прочитано: 215 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
