В зависимости от вида системы ограниченийразличают три основные формы задачи ЛП: общая; стандартная; каноническая

Общей задачей ЛП называется задача, в которой имеются ограничения в виде уравнений и неравенств, причем требование неотрицательности может быть наложено не на все переменные. Математически это записывается следующим образом:

или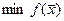

при ограничениях

();

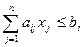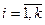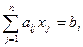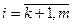();k<m, где m- число ограничений.

(),

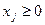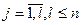где 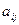, , 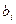, , 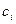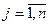- заданные постоянные величины.

Стандартной задачей ЛП называется задача максимизации значения функции 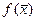при ограничениях, заданных неравенствами, и неотрицательности всех переменных:

при ограничениях вида

();

().

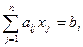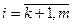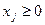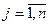Для канонической задачи ЛП требуется максимизировать значение функции 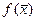, причем все переменные неотрицательны, а ограничения заданы уравнениями:

при ограничениях

();

().

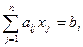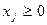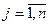Замечание: В канонической задаче ЛП число переменных всегда больше числа уравнений (n > m).

Пояснения: если n = m, то получаем обычную систему линейных уравнений, которая имеет единственное решение в том случае, когда все уравнения линейно независимы 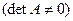, т. е. определитель системы не равен нулю. Если n < m, то часть уравнений линейно зависимы и их можно отбросить, либо противоречивы, и тогда система не имеет допустимых решений.

Рассмотрим способы преобразования задач из одной формы в другую.

1) 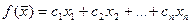эквивалентно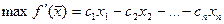

2) Ограничения в виде неравенств можно представить в виде уравнений. Для этого вводятся дополнительные неотрицательные переменные 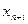(), называемые слабыми переменными. Возможные преобразования:

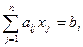() заменяется на

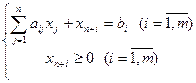
или

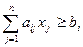() заменяется на

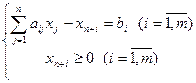
3) Если одно или несколько ограничений в исходной постановке задачи представлены в виде уравнений, то можно перейти к эквивалентной постановке задачи с ограничениями в виде неравенств.

Для этого каждое уравнение вида

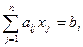
заменяется двумя неравенствами:

; .

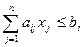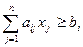Если имеется m неравенств 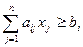(), то их можно заменить на (m + 1) неравенств вида:

()

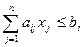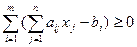
4) Если на переменную 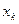не наложено требование неотрицательности, то ее можно заменить двумя переменным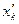и и 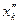, для которых ; ; .

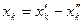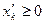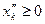В общем случае p таких переменных 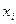(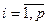) можно заменить на р + 1 неотрицательных переменных , 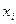(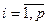), для которых: 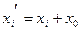, тогда ();

(); .

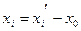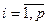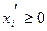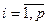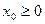Пример: ограничения вида

()

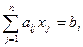можно заменить на ограничения:

();

();

.

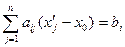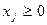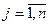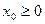Таким образом, задача ЛП всегда может быть приведена к каноническому виду, для которого разработаны алгоритмы решения.