 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теоретические сведения. Точечные оценки параметров распределения
|
|
Точечные оценки параметров распределения.
Пусть дана выборка малого объема п и xi – значения случайного признака Х в выборке. Тогда точечные оценки параметров распределения вычисляются по формулам:
- выборочная средняя
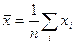 (1)
(1) - исправленная выборочная дисперсия и среднее квадратическое отклонение
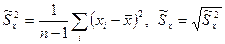 (2)
(2) - выборочная асимметрия
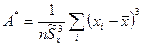 (3) и эксцесс
(3) и эксцесс 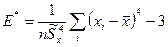 (3а)
(3а) - выборочный коэффициент вариации
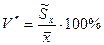 (4)
(4)
Ниже приведен пример вычисления выборочной средней и дисперсии случайного признака при объеме выборки п =9.
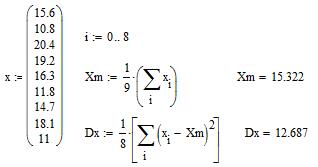
Для выборки большого объема, заданной в виде случайного вектора х с п координатами xi, точечные оценки определяются через начальные моменты распределения:
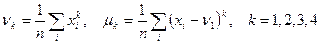 . (5)
. (5)
С учетом введенных обозначений
- выборочная средняя
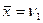 ;
; - выборочная дисперсия и среднее квадратическое отклонение
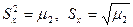 ;
; - выборочная асимметрия
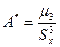 и эксцесс
и эксцесс 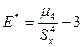 ;
; - выборочный коэффициент вариации
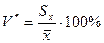 .
.
Чтобы вычислить моду и медиану распределения, необходимо составить вариационный ряд. Для этого требуется:
а) найти min (x) и шах(х), вычислить размах вариации R = шах(х) – min (x) и, округлив R в сторону увеличения, определить число разрядов вариационного ряда k = 5∙1g(п) и шаг ряда h = R/k. Количество разрядов (интервалов) вариационного ряда обычно берут от 8 до 16, причем так, чтобы шаг ряда по возможности был целым числом (или дробным, но удобным для нахождения середины интервала);
б) выбрать левую границу первого интервала х (0) ≤ min(x) и составить интервалы вариационного ряда; для этого надо ввести новый индекс j:= 1 ..k + 1 и оператор
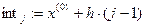 (6)
(6)
При этом последняя k -я граница х (k) должна быть чуть больше или равна шах(х).
в) определить частоту тi признака Х для каждого i -гo интервала; для этого с помощью функции hist(int,x) составить вектор частот. Аргументы: int – вектор, содержащий границы интервалов в порядке их возрастания; x – множество значений некоторой величины, которые распределяются по интервалам, заданным в векторе int. Функция hist возвращает вектор, содержащий в качестве элементов количество точек из x, попавших в соответствующий интервал из int:
m:=hist(int, x); (7)
г) составить дискретный ряд; с этой целью ввести новую переменную 1:= 1.. k и вычислить дискретные значения признака
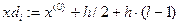 . (8)
. (8)
Интервальные оценки параметров распределения.
Если известно, что случайный признак в генеральной совокупности распределен по нормальному закону N (a, σ), то при малом объеме выборки для интервальной оценки генеральной средней используется стандартное t -распределение Стьюдента, а для интервальной оценки генеральной дисперсии – χ 2-распределение.
При заданной доверительной вероятности α=0.95 и числе степеней свободы ν = n –1 из таблицы распределения Стьюдента находят соответствующее значение t α и составляют доверительный интервал для генеральной средней:
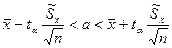 (9)
(9)
При той же доверительной вероятности α и числе степеней свободы ν из таблицы χ 2-распределения находят значения 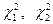 для p 1=0.5(1– α), p 2=0.5(1+ α) соответственно и вычисляют границы доверительного интервала для генеральной дисперсии:
для p 1=0.5(1– α), p 2=0.5(1+ α) соответственно и вычисляют границы доверительного интервала для генеральной дисперсии:
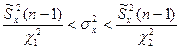 (10)
(10)
В том случае, когда объем выборки достаточно велик, выборочная средняя 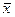 распределена асимптотически нормально, и интервальная оценка генеральной средней выглядит аналогично формуле (9), но величину t находят из таблицы интегральной функции Лапласа:
распределена асимптотически нормально, и интервальная оценка генеральной средней выглядит аналогично формуле (9), но величину t находят из таблицы интегральной функции Лапласа:
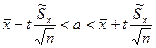 , (11)
, (11)
где 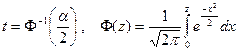 .
.
Дата публикования: 2015-09-17; Прочитано: 246 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
