 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теоретические сведения. Системой линейных алгебраических уравнений (СЛАУ) из m уравнений с n переменными называется система уравнений следующего вида:
|
|
Системой линейных алгебраических уравнений (СЛАУ) из m уравнений с n переменными называется система уравнений следующего вида:
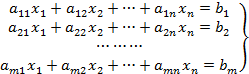 (1)
(1)
Здесь числа  – коэффициенты,
– коэффициенты, 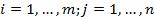 , числа
, числа 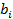 – свободные члены,
– свободные члены, 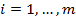 ;
; 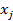 – переменные (неизвестные). Введем следующие матрицы:
– переменные (неизвестные). Введем следующие матрицы:
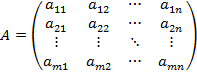 (2)
(2)
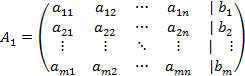 (3)
(3)
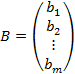 (4)
(4)
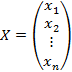 (5)
(5)
Здесь (2) – матрица системы (1), (3) – расширенная матрица системы, (4) – матрица (вектор) свободных членов (правой части системы), (5) – матрица (вектор) переменных (неизвестных).
Тогда система (1) может быть записана в матричном виде:
А∙Х = В (6).
Множество чисел 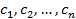 называется решением СЛАУ (1), если при их подстановке в систему (1) вместо соответствующих
называется решением СЛАУ (1), если при их подстановке в систему (1) вместо соответствующих 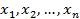 , они приводят эту систему к тождествам. Если
, они приводят эту систему к тождествам. Если 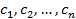 является решением системы (1), то матрица
является решением системы (1), то матрица 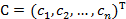 называется вектором решений системы (6).
называется вектором решений системы (6).
Далее будем рассматривать СЛАУ с квадратной матрицей А, у которой m=n. Если det(A) ≠ 0, то система (1) имеет единственное решение. Для его нахождения можно использовать следующие основные способы.
1) Матричный метод (метод обратной матрицы). Рассмотрим систему (1), записанную в виде (6). Для вычисления матрицы неизвестных переменных Х нужно найти матрицу, обратную к А, и умножить ее слева на матрицу свободных членов В:
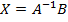 (7).
(7).
2) Метод Крамера. Вычислим определители | Aj |, которые получаются из | A | заменой ее j -го столбца вектором свободных членов В:
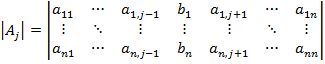 .
.
Тогда элементы вектора неизвестных переменных хj вычисляются по формуле:
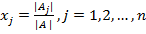 (8).
(8).
3) Метод Гаусса. Он состоит в последовательном исключении неизвестных переменных системы (1) и ее приведению к ступенчатому (или треугольному) виду
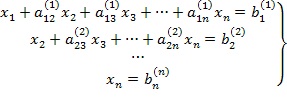
(9).
с последующим нахождением неизвестных переменных в обратном порядке. Процесс перехода от системы (1) к системе (9) называется прямым ходом метода Гаусса. Процесс последовательного нахождения значений неизвестных переменных из систем (9) называется обратным ходом метода Гаусса. Осуществляя обратный ход, из предпоследнего уравнения мы найдем 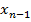 (с учетом последнего уравнения). Зная
(с учетом последнего уравнения). Зная 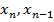 , найдем
, найдем 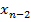 и так далее, пока не найдем последнюю переменную
и так далее, пока не найдем последнюю переменную 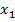 из первого уравнения системы (9).
из первого уравнения системы (9).
Пример решения СЛАУ матричным методом:
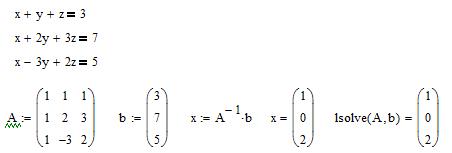
Пример решения СЛАУ методом Крамера:


Пример решения СЛАУ методом Гаусса:

Существуют разные подходы к определению понятия «вектор» в зависимости от области применения этого математического объекта. Наиболее общее определение вводит вектор как упорядоченное множество. Элементы этого множества называются элементами или компонентами вектора. Элементы вектора могут иметь разную природу. Это могут быть числа, функции, другие векторы или матрицы, и другие математические объекты.
Более привычное определение рассматривают вектор с геометрической точки зрения, и вводит его как направленный отрезок. При этом он будет определятся упорядоченной парой точек А и В, причем первая точка А определяет начало вектора, а вторая точка В – его конец. Вектор обычно обозначают либо 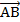 (первой пишется начальная точка), либо
(первой пишется начальная точка), либо 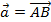 , либо жирным шрифтом: α. Вводят также нулевой вектор, у которого точки начала и конца совпадают. Обозначают его
, либо жирным шрифтом: α. Вводят также нулевой вектор, у которого точки начала и конца совпадают. Обозначают его  . На чертеже вектор обозначают стрелкой:
. На чертеже вектор обозначают стрелкой: 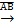 или
или 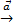 . Начало вектора называется точкой его приложения. Расстояние между началом и концом вектора называют его длиной или модулем. Длина вектора обозначается |
. Начало вектора называется точкой его приложения. Расстояние между началом и концом вектора называют его длиной или модулем. Длина вектора обозначается |  | или |
| или |  |.
|.
Векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Векторы называются компланарными, если существует плоскость, которой они параллельны. Нулевой вектор считается коллинеарным любому вектору и имеет длину, равную нулю. Два вектора называются равными, если они коллинеарные, одинаково направлены и имеют одинаковые длины.
Обычно вектор определяется с точностью до точки приложения. Это означает, что выбрав любую точку 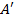 , мы можем построить вектор
, мы можем построить вектор 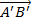 (причем только один!), равный заданному вектору
(причем только один!), равный заданному вектору  , т.е. перенести вектора
, т.е. перенести вектора  в точку
в точку 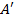 : По сути, мы получим тот же вектор
: По сути, мы получим тот же вектор  , просто приложенный в другой точке
, просто приложенный в другой точке 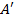 . Таким образом, каждый вектор фактически определяет бесконечное множество равных ему векторов, приложенных в разных точках.
. Таким образом, каждый вектор фактически определяет бесконечное множество равных ему векторов, приложенных в разных точках.
Примечание. Однако, в ряде случаев, например, при использовании векторов в физике, отождествление равных векторов недопустимо. Например, одинаковые силы, описываемые равными векторами, но приложенные в разных точках, могут производить разные действия.
Операции над векторами.
1) Сложение векторов. Пусть существуют векторы 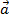 и
и 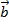 . Постоим равные им векторы
. Постоим равные им векторы 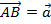 и
и 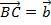 (т.е. перенесем конец
(т.е. перенесем конец 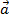 и начало
и начало 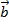 в одну точку В). Тогда вектор
в одну точку В). Тогда вектор 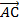 называется суммой
называется суммой  и
и 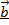 и обозначается
и обозначается 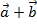 .
.
Примечание. Если выбрать вместо В другую точку 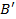 , то в качестве суммы получим вектор
, то в качестве суммы получим вектор 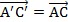 .
.
2) Умножение вектора на число. Произведение вектора 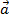 на вещественное число α есть вектор
на вещественное число α есть вектор 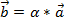 , удовлетворяющий условиям:
, удовлетворяющий условиям:
а) 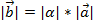 ;
;
б) 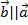 ;
;
в) Если α>0, то  направлены одинаково; если α<0, то
направлены одинаково; если α<0, то  направлены противоположно. Если α=0, то
направлены противоположно. Если α=0, то  .
.
Выражение вида 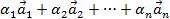 называется линейной комбинацией векторов
называется линейной комбинацией векторов 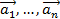 . Числа
. Числа 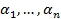 называются коэффициентами линейной комбинации. Линейная комбинация векторов называется тривиальной, если ее коэффициенты равны нулю. Линейная комбинация векторов называется нетривиальной, если как минимум один ее коэффициент не равен нулю. Тривиальная линейная комбинация любых векторов равна
называются коэффициентами линейной комбинации. Линейная комбинация векторов называется тривиальной, если ее коэффициенты равны нулю. Линейная комбинация векторов называется нетривиальной, если как минимум один ее коэффициент не равен нулю. Тривиальная линейная комбинация любых векторов равна 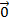 .
.
Векторы 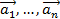 называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная нулевому вектору. Векторы
называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная нулевому вектору. Векторы 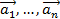 называются линейно независимыми, если равна нулевому вектору только их тривиальная линейная комбинация, т.е. из
называются линейно независимыми, если равна нулевому вектору только их тривиальная линейная комбинация, т.е. из  следует
следует 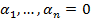 .
.
Свойства линейной зависимости векторов.
1) Система векторов линейно зависима тогда и только тогда, когда один из векторов системы раскладывается в линейную комбинацию остальных.
2) Любые два коллинеарных вектора линейно зависимы, и любые два линейно зависимых вектора коллинеарны.
3) Любые три компланарных вектора линейно зависимы, и любые три линейно зависимых вектора компланарны.
Базис в n-мерном пространстве составляют любые n линейно независимых векторов, взятые в определенном порядке. Любой вектор может быть представлен линейной комбинацией векторов, составляющих базис (базисных векторов). Это называется разложением вектора по базису. Коэффициенты этой линейной комбинации называются координатами или компонентами вектора. Компоненты вектора в каждом базисе будут определены однозначно.
Пример. Пусть заданы векторы 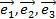 – базис в пространстве, и некоторый вектор
– базис в пространстве, и некоторый вектор  . Тогда
. Тогда 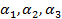 – координаты (компоненты) вектора
– координаты (компоненты) вектора  в данном базисе:
в данном базисе: 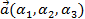 .
.
Свойства компонентов вектора.
1) Равные векторы имеют одинаковые компоненты.
2) При умножении вектора на число все его компоненты умножаются на это число.
3) При сложении векторов складываются их соответствующие компоненты.
Рассмотрим точки А и В. Тогда, чтобы найти компоненты вектора 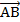 , нужно из координат его конечной точки вычесть соответствующие координаты его начальной точки.
, нужно из координат его конечной точки вычесть соответствующие координаты его начальной точки.
Скалярное произведение векторов  и
и 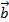 – это число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение обозначается
– это число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение обозначается  ∙
∙ 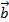 или (
или ( ,
, 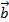 ). По определению
). По определению  ∙
∙ 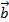 = |
= |  |∙|
|∙| 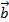 |∙cos(
|∙cos(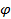 ), где
), где 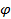 – угол между
– угол между  и
и 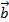 .
.
Свойства скалярного произведения:
1) 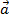 ∙
∙ 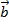 =
= 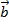 ∙
∙ 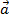
2) (α∙ 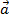 )∙
)∙ 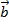 = α∙(
= α∙(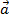 ∙
∙ 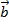 )
)
3) (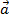 +
+ 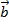 )∙
)∙ 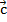 =
= 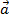 ∙
∙ 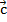 +
+ 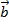 ∙
∙ 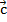
4) 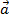 ∙
∙ 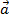 =|
=| 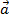 |2≥0.
|2≥0. 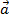 ∙
∙ 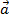 =0 тогда и только тогда, когда
=0 тогда и только тогда, когда 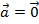 .
.
5) 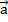 ∙
∙ 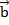 =0, если векторы
=0, если векторы 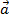 и
и 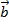 ортогональны, или хотя бы один из векторов
ортогональны, или хотя бы один из векторов 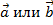 – нулевой.
– нулевой.
Вычисление скалярного произведения через координаты векторов.
Пусть существует 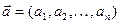 и
и 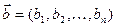 . Тогда
. Тогда 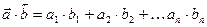 . Из свойства 4) следует, что
. Из свойства 4) следует, что 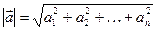 . Из определения скалярного произведения следует, что
. Из определения скалярного произведения следует, что 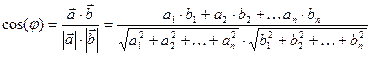 .
.
Три вектора называются упорядоченной тройкой векторов, если указано, какой из них является первым, вторым или третьим. Упорядоченная тройка некомпланарных векторов называется правой, если из конца третьего вектора кратчайший поворот от первого ко второму вектору виден против часовой стрелки, и левой, если этот поворот виден по часовой стрелке.
Векторное произведение векторов  и
и 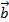 – вектор
– вектор  , удовлетворяющее условиям:
, удовлетворяющее условиям:
1) |  | = |
| = |  |∙|
|∙| 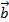 |∙cos(
|∙cos(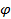 ), где
), где 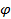 – угол между
– угол между  и
и 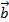 ;
;
2) вектор  ортогонален векторам
ортогонален векторам  и
и 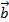 ;
;
3) вектор  направлен так, что тройка векторов
направлен так, что тройка векторов  ,
, 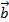 ,
,  является правой.
является правой.
Векторное произведение обозначается 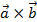 или
или 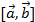 .
.
Свойства векторного произведения:
1) Векторное произведение 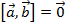 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 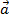 и
и 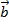 коллинеарны.
коллинеарны.
2) Модуль векторного произведения 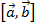 неколлинеарных векторов
неколлинеарных векторов 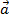 и
и 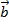 равен площади параллелограмма, построенного на приведенных к общему началу векторах
равен площади параллелограмма, построенного на приведенных к общему началу векторах 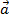 и
и 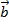 .
.
3) 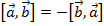 .
.
4) [α∙ 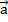 ,
, 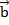 ] = α∙[
] = α∙[ 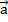 ,
, 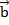 ].
].
5) [ 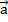 +
+ 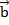 ,
, 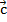 ]=[
]=[ 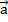 ,
, 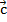 ]+[
]+[ 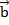 ,
, 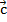 ].
].
Вычисление векторного произведения через координаты векторов.
Пусть заданы 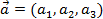 ,
, 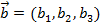 . Тогда координаты вектора
. Тогда координаты вектора 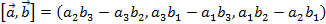 . Для удобства запоминания, можно использовать формулу:
. Для удобства запоминания, можно использовать формулу: 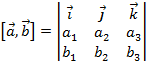 . Тогда разложение этого определителя по первой строке равно:
. Тогда разложение этого определителя по первой строке равно: 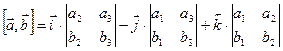 .
.
Смешанное произведение векторов  ,
, 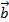 ,
,  – это число
– это число  ∙[
∙[ 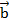 ,
,  ] = [
] = [ 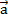 ,
, 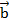 ]∙
]∙  . Смешанное произведение обозначается
. Смешанное произведение обозначается  .
.
Свойства смешанного произведения.
1)  .
.
2) Смешанное произведение 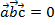 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы  – компланарны.
– компланарны.
3) Смешанное произведение 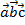 равно объему параллелепипеда, построенного на приведенных к общему началу векторах
равно объему параллелепипеда, построенного на приведенных к общему началу векторах  , взятому со знаком «+», если упорядоченная тройка (
, взятому со знаком «+», если упорядоченная тройка ( ) – правая, и со знаком «–», если она левая.
) – правая, и со знаком «–», если она левая.
Вычисление смешанного произведения через координаты векторов.
Пусть 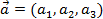 ,
, 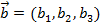 ,
, 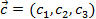 . Тогда смешанное произведение может быть вычислено по формуле:
. Тогда смешанное произведение может быть вычислено по формуле: 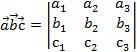 .
.
Рассмотрим следующий пример, иллюстрирующий различные операции над векторами.
Пример. По координатам точек А, В и С для указанных векторов найти модуль вектора  и скалярное произведение векторов
и скалярное произведение векторов  и
и 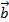 .
.
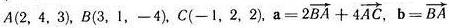
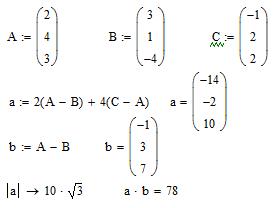
Ниже приведен пример вычисления различных видов произведения векторов.
Пример. По координатам точек А, В и С для указанных векторов найти косинус угла между векторами  и
и 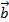 , векторное произведение векторов
, векторное произведение векторов  и
и 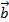 , смешанное произведение векторов
, смешанное произведение векторов  ,
, 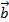 и
и  +
+ 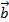 .
.
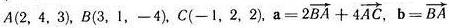
Дата публикования: 2015-09-17; Прочитано: 646 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
