Означення векторного добутку. Основні властивості даної операції та її застосування до розв’язування задач

Нехай у просторі задано два вектори та . Використовуючи дані вектори, знайдемо третій вектор, який задовольняє певним умовам – так званий векторний добуток векторів та . Оскільки нам доведеться користуватись поняттям однакової орієнтованості двох трійок векторів, введемо наступне означення.

Означення 2. Нехай задано впорядковану трійку не компланарних векторів 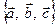, відкладених із спільного початку. Із кінця третього вектора розглядається поворот першого з них до суміщення з напрямком другого вектора найкоротшим шляхом (тобто на кут, який не перевищує 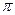). Якщо цей поворот здійснюється за годинниковою стрілкою, то кажуть, що це вліво орієнтована трійка векторів, а коли проти – вправо орієнтована трійка. На рисунку 4_а зображена вліво орієнтована, а на рисунку 4_б – вправо орієнтована трійка векторів .

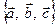Означення 3. Дві впорядковані трійки векторів 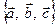та 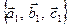називаються однаково орієнтованими, якщо вони одночасно орієнтовані вправо або вліво.

Означення 4. Вектор 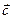називається векторним добутком векторів та , якщо він задовольняє наступні умови:

1) вектор 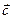ортогональний до кожного із векторів та ;

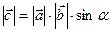2) , де 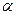– кут між векторами та ;

3) трійки векторів 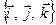та 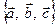однаково орієнтовані (рис. 5). Векторний добуток векторів та позначають символом 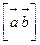або .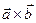

Безпосередньо із означення випливають наступні властивості векторного множення.

Властивість 1. 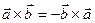(антикомутативність векторного множення).

Властивість 2. Довжина вектора 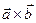дорівнює площі паралелограма, побудованого на векторах та .

Властивість 3. Векторний добуток двох ненульових векторів рівний нульовому вектору тоді і тільки тоді, коли вони колінеарні.

Доведення властивості 1 фактично випливає з третьої умови означення, оскільки перші дві умови виконуються одночасно для векторів 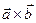та 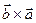. При перестановці у векторному добутку двох множників поворот першого з них до суміщення з напрямком другого вектора найкоротшим шляхом здійснюється в протилежному напрямку. Оскільки вектори 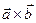та 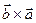колінеарні (обидва одночасно перпендикулярні до векторів та ), мають однакові довжини та протилежно напрямлені, то = .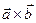

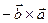Властивість 2 випливає із формули, яка виражає площу паралелограма через дві сторони та кут між ними та відома із шкільного курсу геометрії.

Щоб довести властивість 3 зауважимо, що якщо вектори та колінеарні, то кут між ними дорівнює 0 або 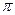. В обох випадках, оскільки 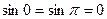, то 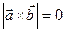. Навпаки, якщ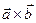о = , то 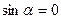, оскільки 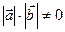. Тому вектори та колінеарні.

Властивість 4. Для векторів ортонормованого базису виконуються наступні рівності:

, , , .

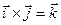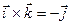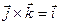Для формулювання та доведення інших властивостей векторного добутку виведемо співвідношення, яке дозволяє знаходити координати вектора 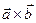через координати векторів та .

Нехай у базисі 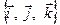вектори та задані своїми координатами: 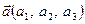, 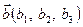. Вважатимемо, що 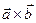= 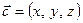. Згідно з умовою 1) означення маємо ^ 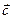та ^ 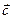, тому 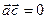та 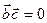. Одержані рівності запишемо у вигляді системи

,

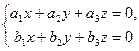розв’язуючи яку, дістаємо

, , ,

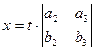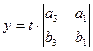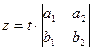де 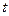– довільне дійсне число. Для відшукання значення 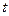використаємо другу умову означення:

=

=

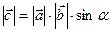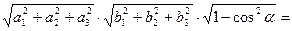
= . (5)

З іншого боку

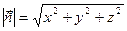
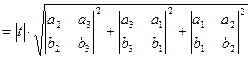. (6)

Легко перевірити, що підкореневі вирази у записах (5) та (6) рівні, тому 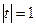, звідки 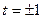. Щоб вибрати з двох одержаних значень 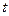потрібне, використаємо відомий з курсу лінійної алгебри факт, що визначник матриці переходу від одного базису до іншого відмінний від нуля. При цьому базиси будуть однаково орієнтовані тоді і тільки тоді, коли визначник додатний. 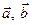Вважатимемо, що вектори та не колінеарні, тому трійка векторів та 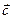утворює базис (у випадку, коли вектори та колінеарні, 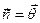, тому необхідність визначення знаку числа 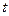відпадає). Знайшовши визначник матриці, складеної із координат векторів 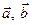та 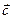, а та вимагаючи, щоб він був додатним, дістаємо

.

Звідси випливає, що число 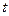додатне, тому 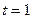. Таким чином,

(, , ).

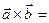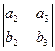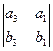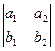Для одержаного вектора часто вибирають іншу, більш зручну для запам’ятання форму запису у вигляді визначника

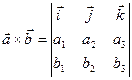. (7)

При цьому координати вектора 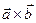обчислюють, як алгебраїчні доповнення до елементів першого рядка.

Перейдемо до вивчення інших властивостей та застосувань векторного добутку.

Властивість 5. .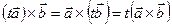

Властивість 6. 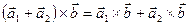(дистрибутивність векторного множення).

Доведення властивостей 5 та 6 випливає із відомих властивостей визначників.

Властивість 7. Площа трикутника, вершини якого розташовані у точках 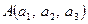, , 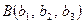, 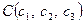обчислюється за формулою

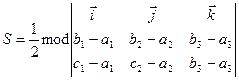. (8)

Справді, оскільки площа паралелограма, побудованого на векторах 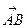та 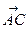, дорівнює 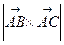і , ,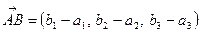

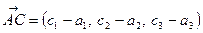то, скориставшись рівністю (7), дістаємо

= .

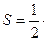
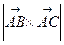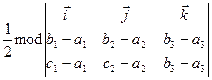Наслідок. Якщо вершини трикутника знаходяться у точках 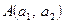, , 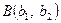, 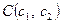то площу трикутника можна обчислити за формулою

.

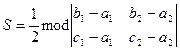Оскільки поняття векторного добутку вводиться тільки у тривимірному просторі, то спочатку помістимо задані вершини у площину тривимірної системи координат 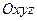, тобто розглянемо точки 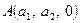, , 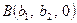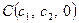. Тепер, скориставшись рівністю (8), дістаємо

= ,

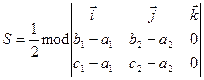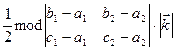
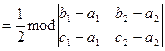що і потрібно було довести.

Розглянемо приклади деяких задач.

Задача 5. Обчислити площу 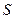паралелограма, побудованого на векторах 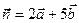та 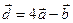, знаючи, що 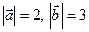, а кут між векторами та дорівнює .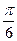

Розв’язання. Використавши доведені властивості 2, 5, 6, дістаємо

.

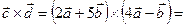
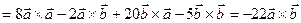Тоді

= .

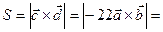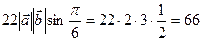Відповідь. 66.

Задача 6. Обчислити відстань 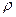від початку координат до прямої, що проходить через точки .

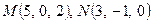Розв’язання. Шукану відстань знайдемо як висоту трикутника 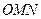, опущену із вершини 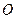. Для цього спочатку обчислимо площу 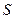трикутника 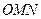. Використовуючи співвідношення (7), дістаємо

= = .

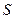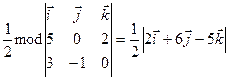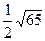Тепер, оскільки 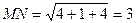, то .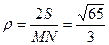

Відповідь. .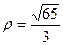

Задача 7. У трикутній піраміді перпендикулярно до кожної грані назовні відносно піраміди проведено вектори, довжина кожного з яких дорівнює площі відповідної грані. Обчислити їхню суму.

Розв’язання. Нехай 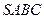– задана піраміда, 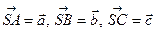, а також 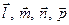– вектори, що задовольняють умову задачі та проведені до граней 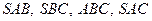відповідно (рис. 6). Обчислимо вектори, як половини векторних добутків векторів, напрямлених по ребрах піраміди. Орієнтацію трійок векторів вибираємо праву. Дістаємо

,

,

.

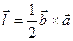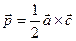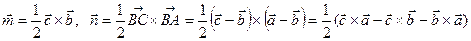Легко перевірити, що сума знайдених векторів дорівнює .