 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Примеры решения задач. 1.2.1.Вычислить определитель второго порядка
|
|
1.2.1. Вычислить определитель второго порядка 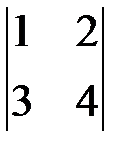 .
.
◄ По формуле (1.1) 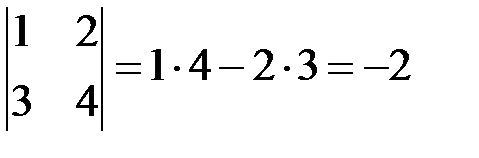 . ►
. ►
1.2.2. Вычислить определитель матрицы 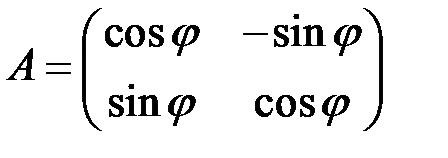 .
.
◄ По формуле (1.1) определитель матрицы
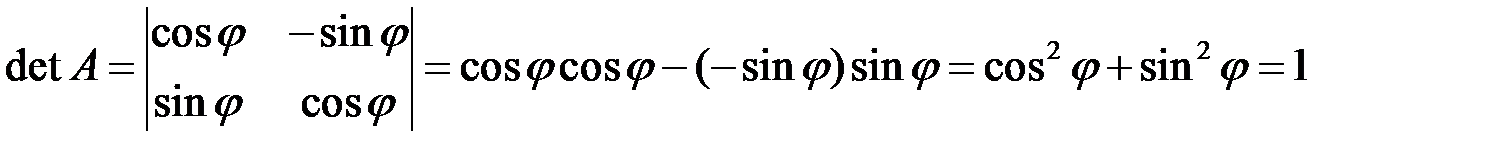 . ►
. ►
1.2.3. Найти алгебраические дополнения элементов первой строки матрицы
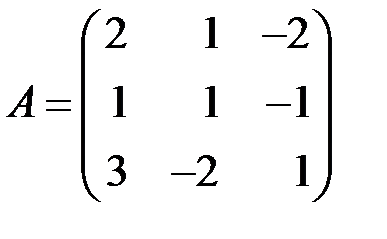 .
.
◄ Алгебраическое дополнение первого элемента первой строки 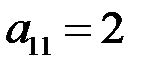 – определитель матрицы, полученной вычеркиванием 1-й строки и 1-го столбца, в которых находится этот элемент, умноженный на
– определитель матрицы, полученной вычеркиванием 1-й строки и 1-го столбца, в которых находится этот элемент, умноженный на 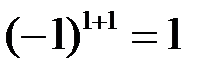 :
: 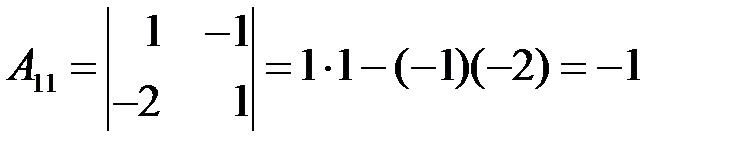 . Алгебраическое дополнение второго элемента первой строки
. Алгебраическое дополнение второго элемента первой строки 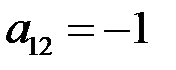 – определитель матрицы, полученной вычеркиванием 1-й строки и 2-го столбца, в которых находится этот элемент, умноженный на
– определитель матрицы, полученной вычеркиванием 1-й строки и 2-го столбца, в которых находится этот элемент, умноженный на 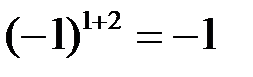 :
: 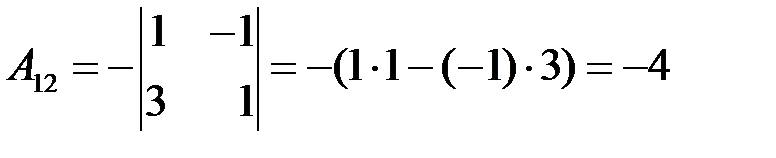 . Алгебраическое дополнение третьего элемента первой строки
. Алгебраическое дополнение третьего элемента первой строки 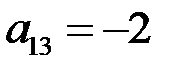 – определитель матрицы, полученной вычеркиванием 1-й строки и 3-го столбца, в которых находится этот элемент, умноженный на
– определитель матрицы, полученной вычеркиванием 1-й строки и 3-го столбца, в которых находится этот элемент, умноженный на 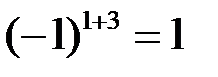 :
:
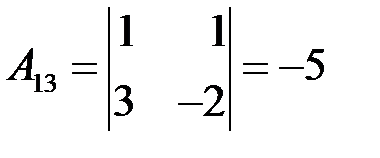 . ►
. ►
1.2.4. Вычислить определитель матрицы 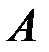 из примера 1.2.3.
из примера 1.2.3.
Решение 1. (по определению – правило треугольников).
◄ 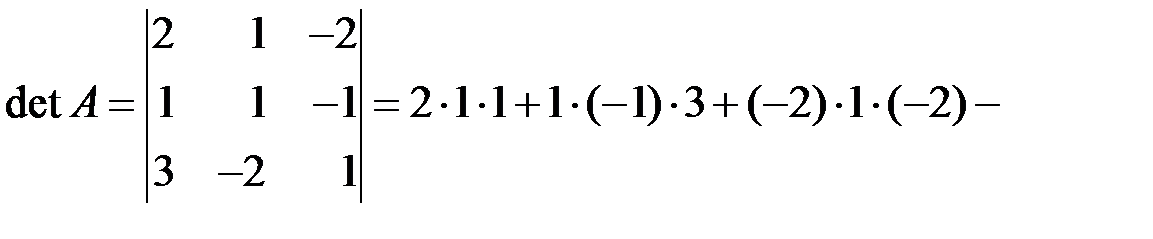
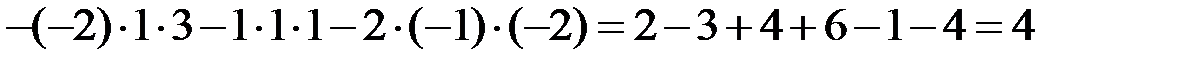 .
.
Здесь первые три слагаемых – произведение элементов, стоящих на главной диагонали и в вершинах двух треугольников, одна из сторон которых параллельна главной диагонали, последние три слагаемых – произведения элементов, стоящих на другой диагонали и в вершинах двух треугольников, одна из сторон которых параллельна этой диагонали, взятые со знаком (–).
►
Решение 2. (разложение по первой строке). ◄ По формуле (1.4) для вычисления определителя надо каждый элемент строки умножить на его алгебраическое дополнение и сложить полученные числа. Алгебраические дополнения элементов первой строки мы уже нашли в примере 1.2.3. Итак,
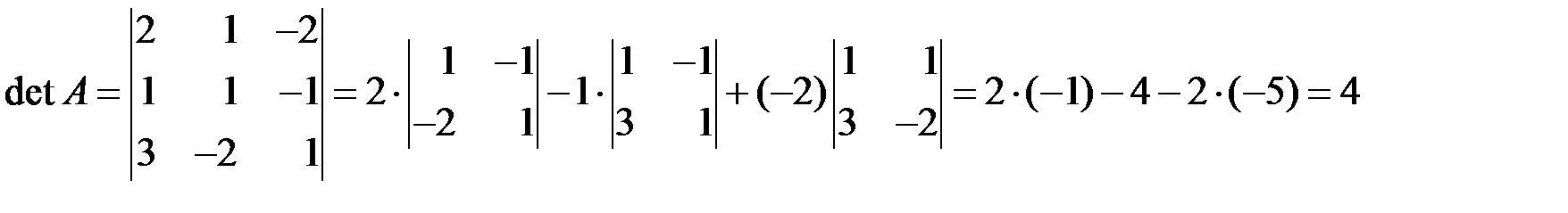 .►
.►
Решение 3. (Метод Гаусса – приведение к треугольному виду).
◄ 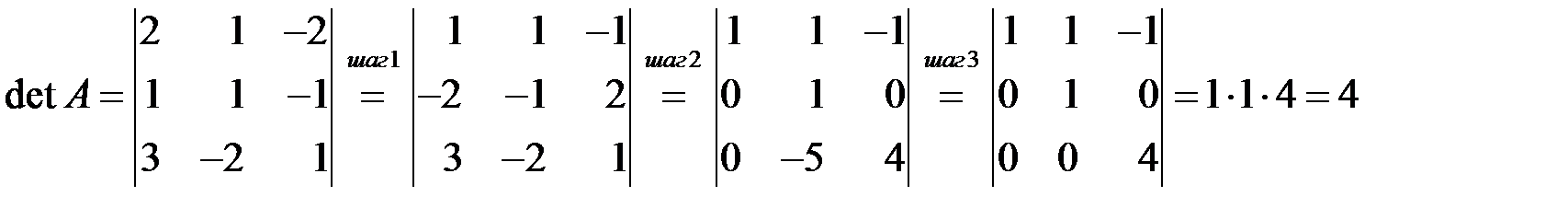
Шаг 1. Поменяли местами 1-ю и 2-ю строки и умножили 2-ю строку на –1. Каждое действие меняет знак определителя (свойства 2-3), в результате определитель не изменится. Цель этих действий – получить в левом верхнем углу единицу (см. замечание 1 в конце решения).
Шаг 2. Ко 2-й строке прибавили 1-ю, умноженную на 2, к 3-й строке прибавили 1-ю, умноженную на (–3). По свойству 7) определитель не изменится. Цель – получить в первом столбце нули ниже первого элемента столбца.
Шаг 3. К 3-й строке прибавили 2-ю, умноженную на 5. Цель – получить во втором столбце нули ниже второго элемента столбца.
В итоге получили определитель треугольной матрицы, равный произведению диагональных элементов. ►
Замечание 1. Если бы мы не сделали 1-й шаг и начали со второго, то пришлось бы ко 2-й строке прибавить 1-ю, умноженную на 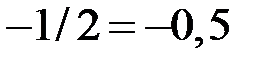 , к 3-й строке прибавить 1-ю, умноженную на
, к 3-й строке прибавить 1-ю, умноженную на 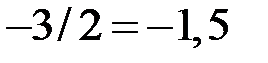 . В итоге пришлось бы работать с десятичными дробями. Если определитель не специально подобран для упражнений, то этого не избежать.
. В итоге пришлось бы работать с десятичными дробями. Если определитель не специально подобран для упражнений, то этого не избежать.
Замечание 2. Для определителя третьего порядка можно опустить шаг 3, разложив определитель, полученный на шаге 2 по первому столбцу:
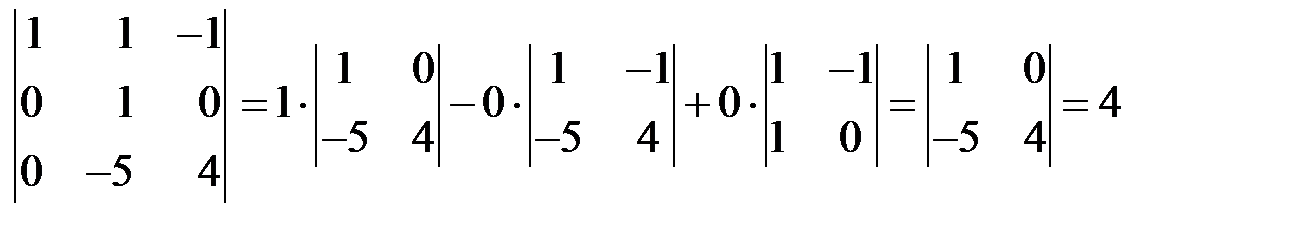 .
.
Конечно, алгебраические дополнения, которые умножаются на нули, ни выписывать, ни считать не нужно. ►
1.2.5. Вычислить определитель матрицы 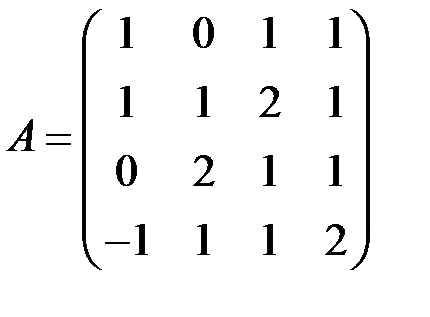 .
.
◄ 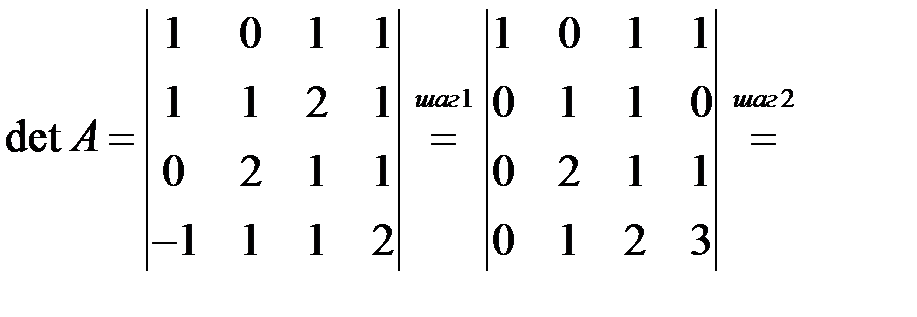
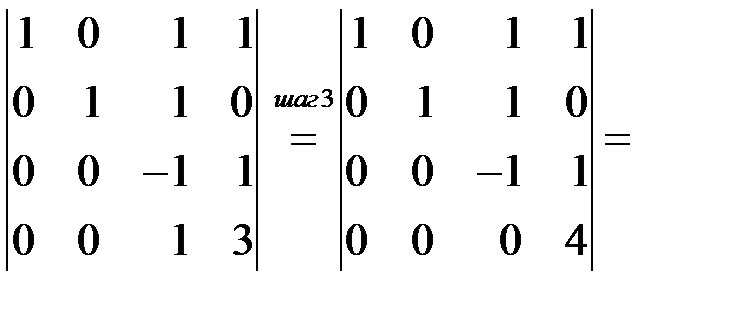
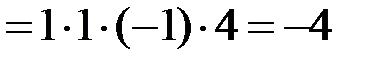 .
.
Шаг 1. Ко 2-й строке прибавили 1-ю, умноженную на –1, 3-ю строку не меняли, к 4-й строке прибавили 1-ю.
Шаг 2. К 3-й строке прибавили 2-ю, умноженную на –2, к 4-й строке прибавили 2-ю, умноженную на –1.
Шаг 3. К 4-й строке прибавили 3-ю. ►
1.2.6. Проверить, что общее определение (1.2) определителя 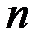 -го порядка при
-го порядка при 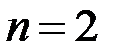 совпадает с формулой (1.1).
совпадает с формулой (1.1).
◄ Согласно (1.2) при 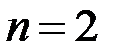
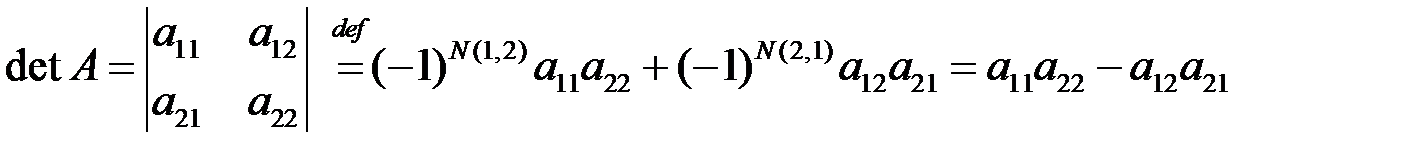 ,
,
где 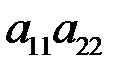 и
и 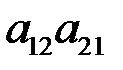 – все возможные произведения по два элемента, взятые из разных строк и разных столбцов, выписанные в порядке возрастания
– все возможные произведения по два элемента, взятые из разных строк и разных столбцов, выписанные в порядке возрастания
номеров строк; 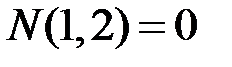 и
и 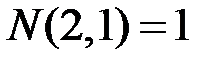 – число инверсий – нарушений естественного порядка в последовательностях
– число инверсий – нарушений естественного порядка в последовательностях 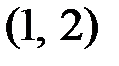 и
и 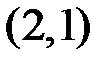 из номеров столбцов. ►
из номеров столбцов. ►
Дата публикования: 2015-09-17; Прочитано: 519 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
