 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Властивості бінарних відношень
|
|
Означення 3.1. Відношення  на множині А називають рефлексивним, якщо для будь-якого а
на множині А називають рефлексивним, якщо для будь-якого а  А виконується (а,a)
А виконується (а,a)  R.
R.
Означення 3.2. Відношення  на множині А називають іррефлексивним, якщо для будь-якого а
на множині А називають іррефлексивним, якщо для будь-якого а  А виконується (а,a)
А виконується (а,a) 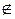
 .
.
Означення 3.3. Відношення R на множині А називають симетричним, якщо для будь-яких а,b  А виконується умова: з того, що (а, b)
А виконується умова: з того, що (а, b) 
 випливає, що (b, а)
випливає, що (b, а)  R.
R.
Означення 3.4. Відношення  на множині А називають антисиметричним, якщо для всіх а,b
на множині А називають антисиметричним, якщо для всіх а,b  А виконується умова: з того, що (а, b)
А виконується умова: з того, що (а, b)  R та (b, а)
R та (b, а) 
 випливає, що a=b. Іншими словами, відношення антисиметричне, якщо в разі а
випливає, що a=b. Іншими словами, відношення антисиметричне, якщо в разі а 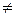 b воно не містить пар (а, b) та (b, а) одночасно.
b воно не містить пар (а, b) та (b, а) одночасно.
Означення 3.5. Відношення  на множині А називають асиметричним, якщо для всіх а,b
на множині А називають асиметричним, якщо для всіх а,b  А виконується умова: з того, що (а, b)
А виконується умова: з того, що (а, b)  R випливає, що (b, а)
R випливає, що (b, а) 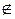
 .
.
Означення 3.6. Відношення  на множині А називають транзитивним, якщо для будь-яких а,b,с
на множині А називають транзитивним, якщо для будь-яких а,b,с  А із того, що (а, b)
А із того, що (а, b)  R
R 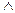 (b, с)
(b, с) 
 випливає (а, с)
випливає (а, с) 
 .
.
Матриця рефлексивного відношення характеризується тим, що всі елементи її головної діагоналі – одиниці, а матриця іррефлексивного відношення – тим, що зазначені елементи є нулями. Зауважимо, що симетричність відношення спричиняє також симетричність матриці. Матриця антисиметричного відношення характеризується тим, що нема жодної пари одиниць на місцях, симетричних відносно головної діагоналі. Матриця асиметричного має таку ж властивість, до того ж всі елементи її головної діагоналі – нулі. Матриця транзитивного відношення характеризується тим, що коли 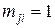 і
і 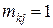 тоді
тоді 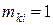 .
.
Важливо зазначити, що властивості симетричності й антисиметричності не є антагоністичними: існують відношення, які одночасно мають ці властивості. Наприклад, відношення  =
= 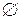 на множині А={а} одночасно й симетричне, і антисиметричне. Є також відношення, які не мають жодної із цих двох властивостей.
на множині А={а} одночасно й симетричне, і антисиметричне. Є також відношення, які не мають жодної із цих двох властивостей.
Приклад 3.1. Розглянемо шість відношень на множині A={1, 2, 3, 4}:
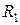 = {(1,1), (1,2), (2,1), (2,2), (3,4), (4,1), (4,4)};
= {(1,1), (1,2), (2,1), (2,2), (3,4), (4,1), (4,4)};
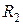 = {(1,1), (1,2), (2,1)};
= {(1,1), (1,2), (2,1)};
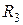 = {(1,1), (1,2), (1,4), (2,1), (2,2), (3,3), (4,1), (4,4)};
= {(1,1), (1,2), (1,4), (2,1), (2,2), (3,3), (4,1), (4,4)};
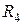 = {(2,1), (3,1), (3,2), (4,1), (4,2), (4,3)};
= {(2,1), (3,1), (3,2), (4,1), (4,2), (4,3)};
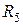 = {(1,1), (1,2), (1,3), (1,4), (2,2), (2,3), (2,4), (3,3), (3,4), (4,4)};
= {(1,1), (1,2), (1,3), (1,4), (2,2), (2,3), (2,4), (3,3), (3,4), (4,4)};
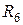 = {(3,4)}.
= {(3,4)}.
Знайти властивості цих відношень.
Відношення 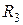 та
та 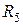 – рефлексивні, оскільки вони містять усі пари вигляду (а,а), тобто (1,1), (2,2), (3,3), (4,4). Решта відношень не є рефлексивними, зокрема,
– рефлексивні, оскільки вони містять усі пари вигляду (а,а), тобто (1,1), (2,2), (3,3), (4,4). Решта відношень не є рефлексивними, зокрема, 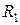 ,
, 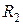 ,
, 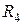 ,
, 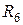 не містять пари (3,3).
не містять пари (3,3).
Відношення 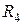 та
та 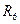 – іррефлексивні, оскільки вони містять усі пари вигляду (а,а), тобто (1,1), (2,2), (3,3), (4,4).
– іррефлексивні, оскільки вони містять усі пари вигляду (а,а), тобто (1,1), (2,2), (3,3), (4,4).
Зауважимо, що 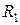 ,
, 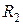 є ні рефлексивними, ні іррефлексивними.
є ні рефлексивними, ні іррефлексивними.
Лише відношення 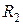 та
та 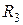 симетричні, тому що містять тільки симетричні елементи.
симетричні, тому що містять тільки симетричні елементи.
Лише відношення 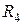 ,
, 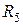 ,
, 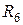 є антисиметричними. У кожному із цих відношень немає таких пар елементів а та b (а
є антисиметричними. У кожному із цих відношень немає таких пар елементів а та b (а 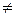 b), що одночасно (а, b)
b), що одночасно (а, b) 
 та (b, а)
та (b, а) 
 .
.
Є також відношення, які не є симетричними, ані антисиметричними. Прикладом такого відношення є 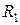 .
.
Зрозуміло, що будь-яке асиметричне відношення повинно бути й антисиметричним. Обернене твердження неправильне. Відношення  5 є антисиметричним відношенням, яке не є асиметричним через те, що воно містить пару (1,1).
5 є антисиметричним відношенням, яке не є асиметричним через те, що воно містить пару (1,1).
Відношення 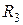 ,
, 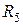 ,
,  6 із є транзитивними. Для кожного з них можна пересвідчитись, що якщо пари (а, b) та (b,с) належать цим відношенням, то й пара (а, с) теж їм належить. Відношення
6 із є транзитивними. Для кожного з них можна пересвідчитись, що якщо пари (а, b) та (b,с) належать цим відношенням, то й пара (а, с) теж їм належить. Відношення 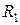 ,
, 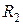 ,
, 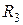 не є транзитивними: (3,4)
не є транзитивними: (3,4) 
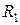 , (4,1)
, (4,1) 
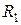 , але (3,1)
, але (3,1) 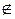
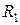 ; (2,1)
; (2,1) 
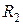 , (1,2)
, (1,2) 
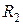 , але (2,2)
, але (2,2) 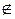
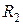 ; (2,1)
; (2,1) 
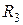 , (1,4)
, (1,4) 
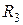 , але (2,4)
, але (2,4) 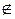
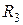 .
.
Дата публикования: 2015-09-17; Прочитано: 7421 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
