ЛЕКЦИЯ 3. 3. Вероятности событий.С каждым случайным событием можно связать некоторое число, называемое вероятностью этого события и обозначаемое (читается:

3. Вероятности событий. С каждым случайным событием 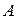можно связать некоторое число, называемое вероятностью этого события и обозначаемое 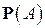(читается: вероятность события 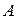; 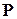– от английского Probability – вероятность). Это число является объективной характеристикой возможностью осуществления события 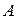в отдельном испытании: чем больше вероятность события 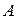, тем чаще наступает это событие при проведении соответствующих испытаний, и наоборот, если вероятность некоторого события мала, то это событие наблюдается редко. Вероятности случайных событий обычно нам неизвестны, но о них мы можем судить по соответствующим частотам. Если провести n опытов, в каждом из которых событие A может наступить или не наступить, то частота осуществления события A, 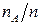, как правило, будет мало отличаться от некоторого числа, которое и является вероятностью 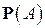. Расхождение между частотой 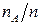и вероятностью 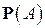будет тем меньше, чем большее число опытов произведено. Если отвлечься от некоторых математических тонкостей, то можно понимать, что вероятность 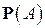– это число, к которому стремится частота 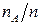при неограниченном возрастании число опытов n:

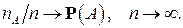
Такое определение вероятности называют статистическим (т. е. по результатам эксперимента).

Так, в примере 1 все частоты выпадения герба мало отличаются от числа 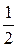, поэтому естественно считать, что вероятность выпадения герба (Г) в отдельном испытании есть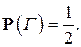

Основные свойства вероятности соответствуют свойствам частоты: поскольку частота любого события всегда неотрицательна и не может быть больше единицы, то для любого случайного события A выполняется условие

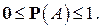
При этом для невозможного события 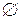его вероятность 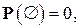а для достоверного события его вероятность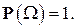

Если 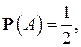то событие 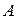наступает примерно в половине всех случаев; если 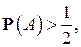то событие 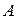наступает чаще, чем не наступает, при 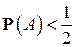мы имеем обратное явление.

Теория вероятностей разрабатывает правила вычисления вероятностей сложных событий по известным вероятностям более простых событий. Одним из основных таких правил является правило сложения вероятностей. Оно формулируется так:

если события A и B несовместны, то вероятность их суммы равна сумме их вероятностей:

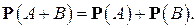(1)

Это свойство вероятности называется аддитивностью.

Если применить это правило к паре противоположных событий A и 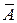, то, поскольку 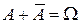, а 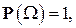имеем формулу

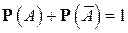
или

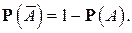(2)

Так что в конкретной задаче следует сначала определиться, вероятность какого события A или 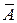проще посчитать.

В общем случае правило (формула) сложения вероятностей имеет вид

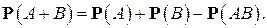(3)

Действительно, так как 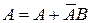и 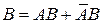, и слагаемые в этих равенствах несовместны, то по свойству аддитивности вероятности можем записать, что

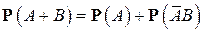и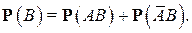

Выражая из второго равенства 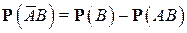и подставляя это в первое, получаем указанную выше формулу (3).

Одновременно мы получаем ещё одно важное свойство вероятности:

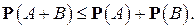(4)

Эта формула обобщается на любое число событий:

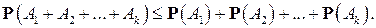
Отметим также, что если 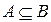, то

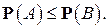
Правило сложения вероятностей (1) обобщается на случай произвольного числа событий: если события 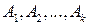попарно несовместны, то

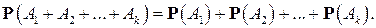(5)

В частности, если события 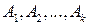образуют полную систему, то

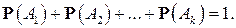
Так, в примере 3 мы имеем полную систему событий 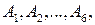поэтому

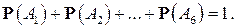
При этом, если кость симметрична, то ясно, что выпадение любой грани равновозможно, т. е. события 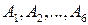имеют одинаковые вероятности (в таких случаях говорят, что события равновероятны). Так как этих событий 6, а сумма их вероятностей равна 1, то вероятность каждого из этих событий равна :

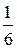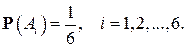
Бросание игральной кости является примером такого эксперимента, когда исходы отдельного испытания образуют полную систему равновероятных событий. Предположение о равновероятности (равновозможности) обычно оправдано в задачах из области азартных игр, лотерей и т. д. Это объясняется тем, что при изготовлении игральных костей, карт и организации лотерей заботятся о соблюдении равновозможности различных исходов. В таких задачах для вычисления вероятностей различных случайных событий применяется так называемое классическое определение вероятности. Приведём его формулировку.

Пусть взаимоисключающими исходами в отдельном испытании некоторого эксперимента являются равновероятные события 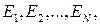т. е. эти события образуют полную систему, и вероятность каждого из них равна 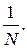Эти события обычно называют элементарными исходами. Если мы интересуемся вероятностью некоторого сложного события вида

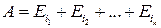
(событие 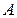происходит, если происходит какой-то из элементарных исходов 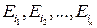), то по правилу сложения вероятностей

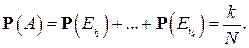(6)

Исходы 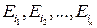, в сумме дающие 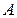, называются благоприятными (для события 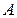) исходами. Таким образом, при классическом определении вероятности вероятность любого события 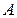равна отношению числа благоприятных для него элементарных исходов к общему числу элементарных исходов.

Пример 4. Бросается игральная кость. Найти вероятность события 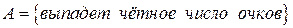. Здесь благоприятными для события 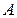исходами являются 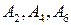(см. пример 3), поэтому по классическому определению вероятности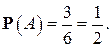

Пример 5. Найти вероятность того, что при бросании одновременно двух игральных костей в сумме выпадет не менее четырёх очков (событие ).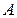

Р е ш е н и е. Здесь число всех возможных исходов опыта есть 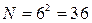и все они равновероятны. Рассмотрим противоположное событие 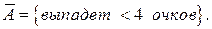Благоприятными для него элементарными исходами являются следующие комбинации очков: (1,1), (1,2) и (2,1). Их всего 3, поэтому по классическому определению вероятности

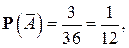следовательно,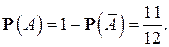

В заключение отметим, что в общей теории для конечных пространств 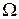(т. е. когда число элементов 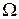конечно) вероятность 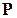определяется как такая неотрицательная числовая функция на алгебре 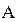подмножеств 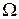: 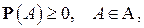что выполняются условие нормировки: 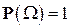и свойство аддитивности (1) (или (5)).

В случае же бесконечных пространств 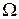должно выполняться более сильное свойство 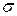- аддитивности:

если события бесконечной последовательности 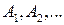элементов 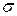- алгебры 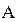подмножеств 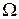попарно несовместны, то

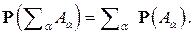
Тройку 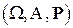называют вероятностным пространством.

Понятие вероятностного пространства содержит лишь самые общие требования, предъявляемые к математической модели случайного явления, и не определяет вероятность 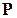однозначно. Дальнейшая конкретизация определения вероятности проводится применительно к рассматриваемой реальной задаче.

4. Простейшие вероятностные схемы. Опишем некоторые часто встречающиеся вероятностные схемы, в которых детализируется приведенное выше классическое определение вероятности.

Пусть имеется урна с N шарами, занумерованными числами 1,2,…, N. Испытание состоит в том, что из этой урны случайно извлекают n шаров и записывают их номера: 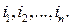Таким образом, исходом испытания (элементарным событием) является комбинация 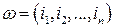, и все исходы считаются равновероятными.

Если каждый вынутый шар сразу возвращается в урну, то такую схему называют схемой случайного выбора с возвращением. В этом случае число всех исходов равно 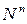(так как каждый номер 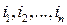может принимать все N значений), и каждый из них имеет одну и ту же вероятность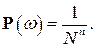

Если же извлекаемые шары в урну не возвращаются, то такую схему называют схемой случайного выбора без возвращения. В таком случае все номера 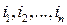различны, поэтому число всех исходов равно 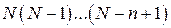(первый номер может принимать все N значений, второй – (N– 1) значений и т. д., n- й номер – 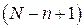значений, конечно, в этом случае должно выполняться условие 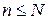). Это число обозначается 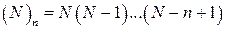и называется числом размещений из N элементов по n. Таким образом, в этой схеме каждый исход имеет вероятность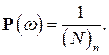

Частный случай размещения при n= N называется перестановкой из N элементов. Число всех перестановок из N элементов равно

,

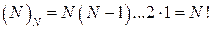так что .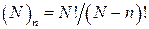

В случае выбора без возвращения можно также считать, что шары извлекаются не по одному, а сразу все. В этом случае не нужно учитывать порядок извлекаемых шаров и, следовательно, элементарным событием теперь является комбинация 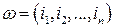, в которой дополнительно выполняется условие 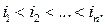Число все таких комбинаций – это число всех подмножеств по n элементов множества N шаров, оно равно числу сочетаний из N элементов по n

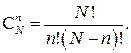
Таким образом, в этой схеме каждый исход имеет вероятность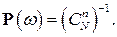

Рассмотрим несколько примеров.

Пример 6. Изурны, содержащей М белых и N – М чёрных шаров, наудачу извлекают сразу n шаров. Какова вероятность того, что в выборке окажется ровно m белых шаров (событие )?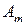

Р е ш е н и е. За элементарные события естественно принять любые подмножества по n элементов, выбранные из множества N шаров, число их равно 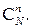Благоприятными для события 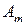будут такие наборы шаров, которые содержат m белых шаров и n – m чёрных шаров. Все такие наборы можно получить следующим образом. Сначала выберем части наборов из белых шаров; число таких частей 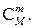Затем отдельно составим части наборов из чёрных шаров; число таких частей 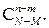Объединяя каждую комбинацию из белых шаров с каждой комбинацией из чёрных шаров, мы получаем полный набор шаров, принадлежащий 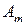. Следовательно, число элементарных событий в 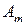равно 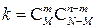, поэтому по классическому определению вероятности (6)

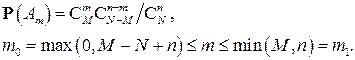(7)

Набор чисел (7) называют гипергеометрическим распределением. Можно показать, что эти числа удовлетворяют условию

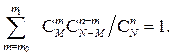
Вычислим теперь вероятность того же события 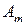в схеме случайного выбора с возвращением. В этом случае число всех элементарных исходов, как указано выше, 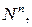а их число в событии 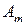можно подсчитать следующим образом. Сначала зафиксируем те места в комбинации ,

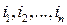на которых должны стоять белые шары – это можно сделать 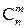различными способами. Далее, на каждое из этих мест можно поставить любой из белых шаров – число различных вариантов равно 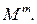Наконец, на каждое из оставшихся 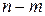мест можно поставить любой из 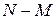чёрных шаров – число вариантов равно 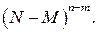Перемножив эти числа, получим искомое число благоприятных для события 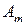исходов: 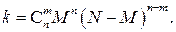Следовательно, по классическому определению вероятности

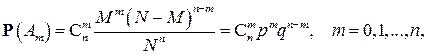(8)

где обозначено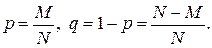

Набор чисел (8) называют биномиальным распределением. Это распределение играет особую в теории вероятностей, и с ним мы будем неоднократно встречаться в последующем.

Пример 7. У человека в кармане n ключей, из которых только один подходит к замку. Ключи последовательно извлекаются (без возвращения) пока не появится нужный ключ. Какова вероятность того, что для этого понадобится m попыток (событие )?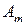

Р е ш е н и е. Будем продолжать извлекать ключи до конца. Тогда элементарным событием будет некоторая последовательность из этих n ключей. Таких последовательностей 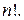Благоприятных же для события 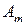последовательностей 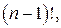так как одно (m -ое) место занято нужным ключом, а остальные 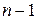ключей можно на оставшиеся 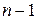мест расставить 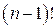способами. Таким образом,

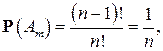
и эта вероятность одна и та же для всех m = 1,2,…, n.

Пример 8 (дни рождения). Какова вероятность 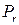того, что дни рождения у r случайно выбранных человек различны? Здесь применима схема выбора с возвращением при N= 365, а число благоприятных для рассматриваемого события исходов равно, очевидно, 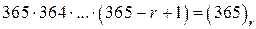, поэтому

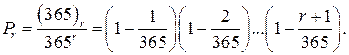
Например, 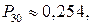так что в группе из 30 человек с вероятностью, большей 0,7, найдутся по крайней мере двое с одним днём рождения.

В разобранных примерах мы имеем дело с конечными вероятностными пространствами, т. е. когда множество 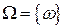конечно. В общем случае модель конечного вероятностного пространства можно задать следующим образом. Пусть заданы неотрицательные числа 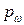такие, что 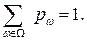Для любого подмножества 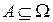вероятность 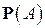определим как сумму

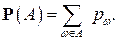
Тогда, как легко видеть, так определённая вероятность (вместе с 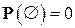) удовлетворяет всем нужным аксиомам. Примером может служить набор чисел (8) (а также (9)), поскольку, согласно биному Ньютона,

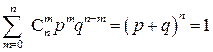
(здесь ).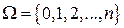

В заключение отметим, что классическое определение вероятности нельзя применить к испытаниям с бесконечным числом «равновероятных» исходов (примером является случайное бросание точки на отрезок). В таких случаях используются так называемые геометрические вероятности, когда вероятность попадания случайной точки в какую-то часть 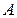области S (на прямой, плоскости и т. д.) пропорциональна мере 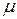(длине, площади и т. д.) этой части: 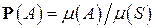. Например, пусть точка случайно бросается на отрезок [0,1]. Тогда вероятность того, что она попадёт левее 0,5 или правее 0,5 равна 0,5.

Эксперимент с бросанием точки на отрезок [0,1] – это модель получения случайных чисел, равномерно распределённых на отрезке [0,1], о чём детальнее мы будем говорить позднее.