 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линейные пространства
|
|
В лекции приведены сведения из курса линейной алгебры, которые востребованы при дальнейшем изложении материала данной учебной дисциплины.
1.1 Метрические пространства
Приведём основные определения теории метрических и нормированных пространств.
Пусть X множество элементов произвольной природы, объединённых по какому-то общему признаку.
Определение 1. Множество X называется метрическим пространством, если любой паре его элементов x и y может быть сопоставлено вещественное число
r(x, y), называемое расстоянием между элементами x и y или метрикой и удовлетворяющее следующим трём аксиомам (неотрицательности, симметричности и треугольника):
Аксиомы метрики.
| 1. r(x, y) ³ 0, причём r(x, y) = 0 Û x = y - неотрицательность; 2. r(x, y) = r(y, x); - аксиома симметричности; 3. r(x, y) £ r(x, z) + r(z, y) для " z Î X – аксиома треугольника. | (1) |
Полнота метрических пространств.
Важнейшим классом метрических пространств являются так называемые полные метрические пространства. Свойство полноты метрических пространств определяется через сходимость последовательностей элементов данных пространств по их метрике.
Определение 2 (сходимость по метрике). Элемент x метрического пространства X называется пределом бесконечной последовательности элементов xn из X, если при n ® ¥ r(xn, x) ® 0. В этом случае говорят, что последовательность (xn) сходится к элементу x по метрике пространства X, и отражают это записью xn ® x или пишут 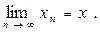
Единственность предела последовательности в метрическом пространстве легко доказывается методом от противного, используя аксиому треугольника.
Определение 3 (фундаментальная последовательность). Последовательность (xn) элементов метрического пространства X называется фундаментальной (или сходящейся в себе), если r(xn, xm) ®0 при n, m ® ¥.
Определение 4. Метрическое пространство X является полным, если в нём всякая фундаментальная последовательность имеет предел.
Определение 5. Две метрики, определённые на одном и том же множестве X, называются эквивалентными, если сходимость последовательности элементов из X по одной из них означает сходимость этой последовательности по другой метрике.
Простейшие примеры метрических пространств.
1. Метрическое пространство Rn.
Простейшим примером метрического пространства является множество Rn всех n - мерных векторов с вещественными координатами, т.е. элементами x, y, z, … пространства Rn служат упорядоченные совокупности из n вещественных чисел:
x = (x 1, x 2, …, xn); y = (y 1, y 2, …, yn); z = (z 1, z 2, …, zn); …
Наиболее употребительными на пространстве Rn являются следующие метрики (2):
Наиболее употребительные метрики на пространстве Rn
a) r(x, y) =  b) r(x, y) =
b) r(x, y) = 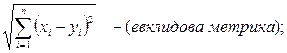 c) r(x, y) =
c) r(x, y) = 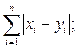
| (2) |
2. Метрическое пространство С [ a, b ].
Пусть X - множество всех вещественнозначных функций x (t), y (t), z (t), … переменной t, которые определены и непрерывны при t Î[ a, b ]. Наиболее употребительными на X являются следующие метрики (3):
Наиболее употребительные метрики на пространстве С [ a, b ]
a) r(x, y) = 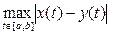 - равномерная метрика, порождающая пространство непрерывных функций, обозначаемое С [ a, b ].
b) r(x, y) = - равномерная метрика, порождающая пространство непрерывных функций, обозначаемое С [ a, b ].
b) r(x, y) = 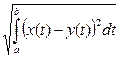 - пространство функций, интегрируемых на отрезке [ a, b ] с квадратом, обозначаемое СL2 [ a, b ].
c) r(x, y) = - пространство функций, интегрируемых на отрезке [ a, b ] с квадратом, обозначаемое СL2 [ a, b ].
c) r(x, y) = 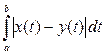 - пространство функций, интегрируемых на отрезке [ a, b ] по модулю, обозначаемое СL [ a, b ]. - пространство функций, интегрируемых на отрезке [ a, b ] по модулю, обозначаемое СL [ a, b ].
| (3) |
1.2 Линейное пространство, нормированное пространство.
Определение 6. Множество X элементов x, y, z, … любой природы называется линейным пространством, если выполнены следующие три требования:
a) Правило сложения элементов. Имеется правило, посредством которого любым двум элементам x и y множества X ставится в соответствие третий элемент z множества X, называемый суммой элементов x и y, обозначаемый символом z = x + y.
b) Правило умножения элемента на число. Имеется правило, посредством которого любому элементу x множества X и любому вещественному числу l ставится в соответствие элемент u множества X, называемый произведением элемента x на число l и обозначаемый символом u = l x или u = x l.
c) Аксиомы линейного пространства. Указанные правила сложения элементов множества X и умножения элемента множества X на число подчиняются следующим восьми аксиомам:
1. x + y = y + x - (переместительное свойство суммы);
2. (x + y) + z = x + (y + z) - (сочетательное свойство суммы);
3. существует нулевой элемент - 0 такой, что x + 0.= x для любого элемента x из множества X (существование и особая роль нулевого элемента);
4. для каждого элемента x из X существует противоположный элемент x ¢ такой, что x + x ¢ = 0 (существование противоположного элемента);
5. любому элементу x множества X и вещественному числу l = 1 ставится в соответствие элемент u = 1× x = x (особая роль числового множителя 1);
6. l (m x) = lm (x) (сочетательное свойство относительно числового множителя);
7. (l + m)× x = lx + m x (распределительное свойство относительно суммы числовых множителей);
8. l (x + y) = l x + l y (распределительное свойство относительно суммы элементов).
Определение 7. Линейное пространство X называется нормированным пространством, если каждому его элементу x ставится в соответствие вещественное число, называемое нормой и обозначаемое 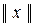 , такое, что оно удовлетворяет следующим трём аксиомам (неотрицательности, однородности, аксиоме треугольника):
, такое, что оно удовлетворяет следующим трём аксиомам (неотрицательности, однородности, аксиоме треугольника):
Аксиомы нормы:
1. 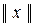 ³ 0, причём ³ 0, причём 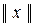 = 0 Û x = 0 - (аксиома неотрицательности);
2. = 0 Û x = 0 - (аксиома неотрицательности);
2. 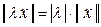 для " l Î R - (аксиома однородности);
3. для " l Î R - (аксиома однородности);
3.  для " x, y Î X -- (аксиома треугольника). для " x, y Î X -- (аксиома треугольника).
| (4) |
Как правило, на линейном пространстве X норма, как и метрика, может быть задана не единственным образом.
Отметим, что имеет место очень важная теорема.
Теорема 1. Всякое нормированное пространство является метрическим пространством.
Доказательство. Действительно, пусть множество X это нормированное пространство с элементами x, y, z, … и заданной нормой 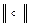 . Покажем, что равенство:
. Покажем, что равенство:
r(x, y) = 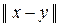 (5)
(5)
задаёт метрику на пространстве X, индуцированную (или ассоциированную с) данной нормой 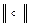 .
.
Для доказательства теоремы, используя аксиомы нормы, подтвердим справедливость аксиом метрики для метрики, заданной (индуцированной) правилом (8).
Первая аксиома метрики: r(x, y) ³ 0, причём r(x, y) = 0 Û x = y;
В данном случае имеем:
r(x, y) = 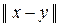 ³ 0, при этом r(x, y) = 0 Û
³ 0, при этом r(x, y) = 0 Û 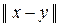 = 0 Û x - y = 0 Û x = y;
= 0 Û x - y = 0 Û x = y;
Вторая аксиома метрики: r(x, y) = 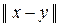 =
= 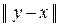 = r(y, x);
= r(y, x);
Действительно, в данном случае имеем:
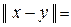
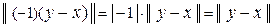 ;
;
Третья аксиома метрики: r(x, y) £ r(x, z) + r(z, y) для " z Î X.
Действительно, в данном случае имеем:
r(x, y) = 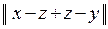 £
£ 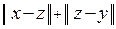 = r(x, z) + r(z, y).
= r(x, z) + r(z, y).
Теорема доказана.
В силу теоремы 1, утверждения, касающиеся метрических пространств, могут быть переформулированы в терминах норм для нормированных пространств.
Если метрическое пространство X с заданной на нём метрикой r(x, y) линейно, (т.е. если для его элементов определены операции сложения элементов и умножения элемента на число, которые должны подчиняться восьми аксиомам линейного пространства), то в нём естественно ввести норму равенством:
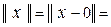 r(x, 0) (6)
r(x, 0) (6)
Равенство (6) позволяет трактовать норму элемента как расстояние от него до нуля (наличие которого обязательно в линейном пространстве).
Необходимо отметить, что из равенства (6) и определения сходимости по метрике (2) следует, что сходимость по метрике последовательности (xn) к элементу x в нормированном пространстве X означает и сходимость по норме, заданной в соответствии с правилом (6), ибо:
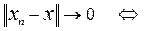 r(xn, x) ® 0 Û xn ® x.
r(xn, x) ® 0 Û xn ® x.
По аналогии с определением 3 (последовательность (xn) фундаментальна в X если r(xn, xm) ®0 при n, m ® ¥), фундаментальность последовательности (xn) в нормированном пространстве X характеризуется требованием: 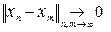 .
.
Определение 8. Нормированное пространство является полным, если в нём всякая фундаментальная последовательность сходится. Полное нормированное пространство называется банаховым (или В – пространством *).
* В - пространства названы в честь польского математика Стефана Банаха - одного из создателей современного функционального анализа.
Простейшие примеры нормированных пространств.
1. Нормированное пространство Rn. Простейшим примером нормированного пространства является рассмотренное выше множество Rn всех n - мерных векторов с вещественными координатами (с определёнными в нём естественным для векторной алгебры образом операциями сложения векторов и умножения вектора на число). Такое множество Rn образует линейное пространство, на основе которого конструируются различные нормированные пространства.
Например, в соответствии с введёнными выше в метрическом пространстве Rn метриками (2) на основе правила (6) для произвольного элемента x = (x 1, x 2,…, xn) из Rn легко ввести нормы вектора, индуцированные соответствующими метриками (2):
Векторные нормы на пространстве Rn
| Метрики на Rn | Норма, индуцированная на Rn метриками, в соответствии с правилом: 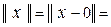 r(x, 0) r(x, 0)
| (7) |
a) r(x, y) = 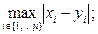 b) r(x, y) =
b) r(x, y) = 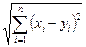 ;
c) r(x, y) = ;
c) r(x, y) = 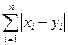 ; ;
| a) 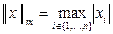 - норма максимум;
b) - норма максимум;
b) 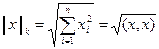 = - евклидова норма;
c) = - евклидова норма;
c) 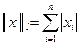 норма - сумма; норма - сумма;
|
Замечание. Отметим, что при определении нормы вектора на пространстве Rn евклидова норма вектора (пункт b) ) может быть определена также через скалярное произведение (x, x) вектора - самого на себя. Как следует из пункта b) в евклидовом пространстве норма вектора равна скалярному произведению вектора самого на себя (т.е. корню квадратному из суммы квадратов его координат) то есть норма вектора равна его длине.
2. Нормированное пространство С [ a, b ]. Другим примером метрического пространства является рассмотренное выше множество X всех вещественнозначных функций x (t), y (t), z (t),… переменной t, которые определены и непрерывны при
t Î[ a, b ]. На данном множестве X всех вещественнозначных функций x (t), y (t), z (t), … переменной t, которые определены и непрерывны при t Î[ a, b ], легко ввести нормы (8), индуцированные соответствующими метриками (3):
| Метрики на С [ a, b ] | Норма, индуцированная на С [ a, b ] метриками, в соответствии с правилом: 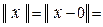 r(x, 0) r(x, 0)
| (8) |
a) r(x, y) = 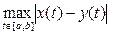 ;
b) r(x, y) = ;
b) r(x, y) = 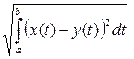 ;
c) r(x, y) = ;
c) r(x, y) = 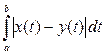 ; ;
| a) 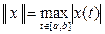 - пространство С [ a, b ];
b) - пространство С [ a, b ];
b) 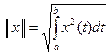 - пространство СL2 [ a, b ];
c) - пространство СL2 [ a, b ];
c) 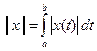 - пространство СL [ a, b ]. - пространство СL [ a, b ].
|
3. Нормированное линейное пространство матриц. Примером нормированного линейного пространства также является множество X всех матриц размерности m ´ n, элементы которых - aij являются вещественными числами.
Если на таком множестве X - матриц размерности m ´ n, традиционным способом определить операцию сложения матриц и умножения матрицы на число, то легко убедиться в справедливости всех пунктов определения линейного пространства для данного множества X.
§2. Действия над матрицами.
2.1 Основные определения. Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов. Числа m и n называются порядками матрицы. В случае если m = n, матрица называется квадратной, а число m = n - её порядком.
Для обозначения матриц используются большие латинские буквы, числа, входящие в состав матрица, обозначаются соответствующими малыми латинскими буквами и называются элементами матрицы. При этом для обозначения матрицы A порядка m = n, с элементами aij (i = 1,2,…, m), (j = 1,2,…, n) используют запись:
A = [ aij ] (i = 1,2,…, m), ( j = 1,2,…, n) или A = 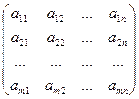 .
.
Во избежание путаницы в дальнейшем, считают, что первый индекс i - обозначает номер строки элемента, а второй индекс j - обозначает номер столбца элемента aij.
Квадратная матрица, диагональная матрица, единичная матрица.
Определение 9. Матрица A = [ aij ] (i = 1,2,…, n), ( j = 1,2,…, n) порядка n ´ n называется квадратной матрицей, т.е. квадратная матрица – это матрица, имеющая равное количество столбцов и строк. Поэтому при обозначении порядка квадратных матриц вместо обозначения n ´ n просто указывают «матрица порядка n». В случае квадратной матрицы вводится понятие главной диагонали матрицы.
Определение 10. Главной диагональю (квадратной) матрицы A = [ aij ] (i = 1,2,…, n),
( j = 1, 2,…, n) порядка n ´ n называется диагональ a 11, a 22, a 33, …,, ann, идущая из левого верхнего угла этой матрицы в правый нижний её угол.
Определение 11. Диагональной матрицей (D) называется квадратная матрица, у которой элементы, расположенные вне главной диагонали, равны нулю. Каждая диагональная матрица порядка n имеет вид:
D = 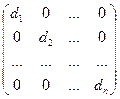 , где d 1, d 2, …, dn – какие угодно числа.
, где d 1, d 2, …, dn – какие угодно числа.
Определение 12. Единичной матрицей n – го порядка называется диагональная матрица порядка n (обозначается символами Е), у которой все элементы, стоящие на главной диагонали, равны единице, т.е. единичной называется матрица токая, что
Е = [ di ] = 1, (i = 1, 2,…, n).
E = 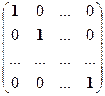 , 0 =
, 0 = 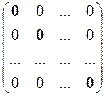 .
.
Определение 13. Нулевой матрицей n – го порядка называется диагональная матрица порядка n (обозначается символами 0), у которой все элементы, в том числе и стоящие на главной диагонали, равны нулю, т.е. нулевой называется матрица, такая, что 0 = [ di ] = 0, (i = 1, 2,…, n).
2.2 Сложение матриц.
Определение 14. Суммой двух матриц A = [ aij ] и B = [ bij ] (i = 1,2,…, m), ( j = 1,2,…, n) одного и того же порядка m ´ n называется матрица C = [ cij ] (i = 1,2,…, m), (j = 1,2,…, n) того же порядка m ´ n элементы cij которой равны:
cij = aij + bij (i = 1,2,…, m), (j = 1,2,…, n). (9)
Для обозначения суммы матриц A и B используется обозначение C = A + B. Итак, в соответствии с определением 14 имеем:
C = A + B = 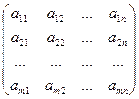 +
+ 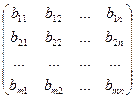 =
= 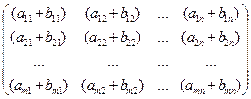
Из определения суммы матриц, а точнее из формулы (9) следует, что операция сложения матриц обладает теми же свойствами, что и операция сложения вещественных чисел, а именно:
1. Переместительным свойством: C = A + B = B + A;
2. Сочетательным свойством: (A + B) + C = A + (B + C).
Очевидно, что если на множестве матриц X сумма матриц определена указанным выше способом, то выполняются аксиомы 1 - 2 из определения 6 линейного пространства.
2.3 Умножение матрицы на число.
Определение 15. Произведением матрицы A = [ aij ] (i = 1,2,…, m), ( j = 1,2,…, n) порядка m ´ n на вещественное число l называется матрица C = [ cij ] (i = 1,2,…, m), (j = 1,2,…, n) того же порядка m ´ n элементы cij которой равны:
cij = laij (i = 1,2,…, m), (j = 1,2,…, n). (10)
Для обозначения произведения матрицы A на число l используется обозначение C = A l = l A.
Непосредственно из формулы (10) следует, что операция умножения матрицы на число обладает следующими свойствами:
1. 1 A = A;
2. (lm ) A = l (m A) (сочетательное свойство относительно числового множителя);
3. (l + m)A = l A + m A (распределительное свойство относительно суммы чисел);
4. l (A + B) = l A + l B (распределительное свойство относительно суммы матриц);
Таким образом заключаем, что в данном случае выполняются требования аксиом
5 – 8 из определения 6 линейного пространства.
Итак, если на множестве матриц X одинаковой размерности m ´ n ввести операции сложения матриц и умножения матрицы на число по указанным выше правилам, то соответствующие требования 1) и 2) (сложения элементов и умножения элемента на число) из определения 6 линейного пространства будут выполнены. Также показано, что свойства введённых операций сложения матриц и умножения матрицы на число удовлетворяют аксиомам 1 - 2 и 5 - 8 из определения 6 линейного пространства.
Для выполнения требований оставшихся аксиом 3 – 4 из определения линейного пространства на множестве матриц необходимо ввести нулевой и обратный элементы.
Так в качестве нулевого элемента 0 = [ aij ] можно выбрать матицу размерности m ´ n, элементами которой являются нули aij. = 0.
В качестве обратного элемента для матрицы A = [ aij ] (i = 1,2,…, m), ( j = 1,2,…, n) порядка m ´ n можно выбрать матрицу A¢ = [ a¢ij ] (i = 1,2,…, m), (j = 1,2,…, n) того же порядка m ´ n с элементами a¢ij = - aij, тогда очевидно, что A + A¢ = 0.
Таким образом, показано, что множество X - матриц размерности m ´ n, с определёнными выше операциями сложения матриц и умножения матрицы на число, а также с введёнными нулевым и обратным элементом, удовлетворяет всем требованиям определения 6 линейного пространства.
2.4 Умножение матриц.
Определение 13. Произведением матрицы A = [ aij ] (i = 1,2,…, m), ( j = 1,2,…, n) порядка m ´ n на матрицу B = [ bij ] (i = 1,2,…, n), ( j = 1,2,…, p) порядка n ´ p называется матрица С = [ сij ] (i = 1,2,…, m), ( j = 1,2,…, p) порядка m ´ p, с элементами сij определяемыми по формуле:
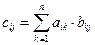 , (i = 1,2,…, m), ( j = 1,2,…, p) (11)
, (i = 1,2,…, m), ( j = 1,2,…, p) (11)
Например, C = A×B = 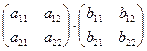 =
= 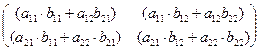
Из сформулированного выше определения произведения матриц вытекает, что матрицу A можно умножить не на всякую матрицу B: необходимо, чтобы число столбцов матрицы A было равно числу строк матрицы B.
Пусть имеется две матрицы A(m´n) и B(k ´ p), тогда для того чтобы определить произведение A×B необходимо, чтобы выполнялось условие n = k, а для того, чтобы определить произведение B×A необходимо, чтобы выполнялось условие p = m.
Поэтому, если оба произведения A×B и B×A существуют одновременно, то это означает, что выполнено условие: n = k и p = m. При этом C = A×B = C(m´p), но
p = m, поэтому получаем, что C(m´m), т.е. C = A×B – квадратная матрица порядка m (при условии, что определено B×A).
Аналогично Z = B×A = Z(k ´ n), но n = k, поэтому получаем, что Z(k ´ k), т.е.
Z = B×A – квадратная матрица порядка k (при условии, что также определено B×A).
В частности оба произведения A×B и B×A одновременно можно определить лишь в том случае, если A и B являются квадратными матрицами одинакового порядка.
Таким образом, если матрицы C = A×B и Z = B×A существуют одновременно, то они обе являются квадратными матрицами (хотя и разного порядка). Таким образом, мы фактически доказали Теорему:
Теорема 2. Для того, чтобы оба произведения A×B и B×A не только были определены, но и имели одинаковый порядок, необходимо и достаточно, чтобы обе матрицы A и B были квадратными матрицами одного и того же порядка.
Свойства произведения матриц.
Из формулы (11) вытекают следующие свойства произведения матрицы A на B матрицу:
1) Сочетательное свойство: (A×B)×C = A×(B×C);
2) Распределительное свойство произведения матриц (относительно суммы матриц) Сочетательное свойство: (A + B)×C = A×C + B×C или
A×(B + C) = A×B + A×C.
3) Перестановочное свойство. Вопрос о равенстве матиц A×B и B×A имеет смысл лишь для квадратных матриц A и B одинакового порядка (ибо, как указывалось выше при доказательстве теоремы 2, только для таких матриц A и B оба произведения A×B и B×A одновременно определены и являются матрицами одинаковых порядков).
Однако, как показывает элементарный пример, что произведение двух квадратных матриц одинакового порядка не обладает, вообще говоря, перестановочным свойством. В самом деле, например, для матриц
A = 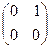 и B =
и B = 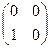 имеем: A×B =
имеем: A×B = 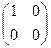 B×A =
B×A = 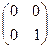 .
.
Поэтому в общем случае произведение матриц не обладает перестановочным свойством. Однако имеют место частные случаи, когда для произведения матриц это перестановочное свойство выполняется.
Определение 14. Две матрицы, для произведения которых справедливо перестановочное свойство, называются коммутирующими матрицам, т.е. если A и B коммутирующие матрицы, то A×B = B×A.
Пусть D диагональная матрица порядка n и A квадратная матрица порядка n:
D = 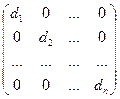 , A =
, A = 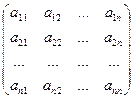
Тогда на основе формулы (11) можно убедиться, что справедливо равенство
A× D = D ×A.
Легко видеть, что определённые выше единичная E и нулевая 0 матрицы порядка n коммутируют друг с другом и с произвольной квадратной матрицей порядка n:
A×E = E×A = A; A×0 = 0×A = 0; 0×E = E×0 = 0.
В заключение отметим, что понятие нулевой матрицы можно ввести и для неквадратных матриц. Нулевой также называют любую матрицу, все элементы которой равны нулю.
2.5 Обратная матрица
Определение 15. Обратной матрицей к квадратной матрице A порядка n, называется квадратная матрица A-1 порядка n такая, что: A-1×A = A×A-1 = Е, где Е - единичная матрица порядка n.
Алгоритм вычисления обратной матрицы A-1 (матрицы, обратной к матрице A).
Пусть A невырожденная квадратная матрица порядка n:
A = 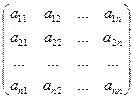 ; где det A =
; где det A = 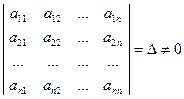 ;
;
Построим для матрицы A присоединённую матрицу 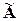 :
: 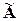 =
= 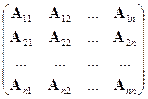 ;
;
где 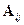 - алгебраические дополнения соответствующих элементов
- алгебраические дополнения соответствующих элементов 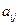 матрицы A.
матрицы A.
Алгебраическим дополнением 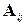 данного элемента
данного элемента 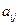 матрицы A называется число равное
матрицы A называется число равное 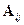 =
= 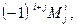 где
где 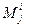 - минор элемента
- минор элемента 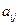 .
.
Минором любого элемента 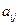 матрицы A n -го порядка называется определитель порядка n - 1, соответствующий той матрице, которая получается из матрицы A в результате вычёркивания i -ой строки и j -ого столбца (т.е. той строки и того столбца, на пересечении которых стоит элемент
матрицы A n -го порядка называется определитель порядка n - 1, соответствующий той матрице, которая получается из матрицы A в результате вычёркивания i -ой строки и j -ого столбца (т.е. той строки и того столбца, на пересечении которых стоит элемент 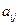 ).
).
Далее для матрицы 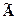 строят транспонированную матрицу
строят транспонированную матрицу 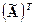 =
= 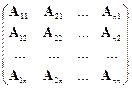 .
.
Разделив все элементы матрицы 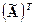 на величину определителя исходной матрицы A, т.е. на D, получаем матрицу:
на величину определителя исходной матрицы A, т.е. на D, получаем матрицу:
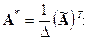
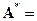
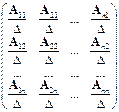
Полученная матрица 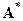 является обратной к матрице A, т.е.
является обратной к матрице A, т.е. 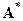 = A-1.
= A-1.
2.6 Норма на линейном пространстве матриц.
Определение 16. Нормой матрицы A = [ aij ] (i = 1,2,…, m), ( j = 1,2,…, n) порядка m ´ n называется действительное число 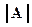 , удовлетворяющее условиям:
, удовлетворяющее условиям:
1. 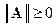 , причём
, причём 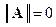 тогда и только тогда, когда A = 0;
тогда и только тогда, когда A = 0;
2. 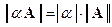 - для любой матрицы A = [ aij ] (i = 1,2,…, m), ( j = 1,2,…, n) порядка m ´ n и любого вещественного числа a. Причём
- для любой матрицы A = [ aij ] (i = 1,2,…, m), ( j = 1,2,…, n) порядка m ´ n и любого вещественного числа a. Причём 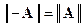 ;
;
3. Для любых двух матриц A = [ aij ] и B = [ bij ] (i = 1,2,…, m), ( j = 1,2,…, n) порядка m ´ n справедливо неравенство треугольника 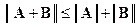 .
.
Для матрицы произвольного типа A = [ aij ] (i = 1,2,…, m), ( j = 1,2,…, n) порядка m ´ n:
наиболее часто используются следующие три легко вычисляемые нормы (12).
Наиболее употребительные нормы матриц
1. 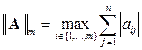 (m - норма) - максимальная сумма модулей элементов строк
матрицы;
2. (m - норма) - максимальная сумма модулей элементов строк
матрицы;
2.  (m - норма) - максимальная сумма модулей элементов столбцов
матрицы;
3. (m - норма) - максимальная сумма модулей элементов столбцов
матрицы;
3. 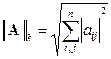 (k - норма) - корень квадратный из суммы квадратов модулей
элементов матрицы. (k - норма) - корень квадратный из суммы квадратов модулей
элементов матрицы.
| (12) |
В частном случае, когда матрица A вырождается в m - мерный вектор x:
x =  , то есть A =
, то есть A = 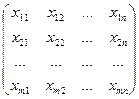 ® x j =
® x j =  , j = 1,2,…, n.
, j = 1,2,…, n.
В этом случае в соответствии с определением матричной нормы получаем следующие нормы вектора x (13), согласованные с приведёнными выше матричными нормами.
Нормы векторов, согласованные с матричными нормами (12).
1. 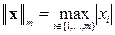 (m – норма) - максимальный модуль элемента вектора;
2. (m – норма) - максимальный модуль элемента вектора;
2. 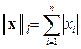 (l – норма) - сумма модулей элементов вектора;
3. (l – норма) - сумма модулей элементов вектора;
3. 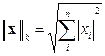 (k - норма) - корень квадратный из суммы квадратов модулей элементов вектора. (k - норма) - корень квадратный из суммы квадратов модулей элементов вектора.
| (13) |
2.7 Понятие определителя. Вычисление определителей 2 и 3 порядков.
Рассмотрим произвольную квадратную матрицу A любого порядка n:
A = 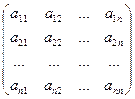 ; (14)
; (14)
С каждой такой матрицей свяжем вполне определённую числовую характеристику, называемую определителем данной матрицы A, и обозначаемую det A:
det A = 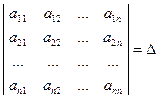 ; (15)
; (15)
Если порядок матрицы A равен единице (n = 1), т.е. матрица состоит только из одного элемента A = (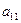 ), то определителем данной матрицы A = (
), то определителем данной матрицы A = (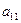 ) первого порядка называется числовая величина элемента
) первого порядка называется числовая величина элемента 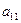 : D =
: D = 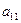 .
.
Если порядок матрицы A равен двум (n = 2), т.е. матрица имеет вид:
A = 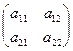 , то det A =
, то det A = 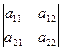 = a 11 a 22 – a 12 a 21 = D (16)
= a 11 a 22 – a 12 a 21 = D (16)
Формула (16) представляет собой правило вычисления определителя второго порядка по элементам соответствующей ему матрицы второго порядка.
Если порядок матрицы A равен трём (n = 3), т.е. матрица A имеет вид:
A = 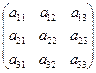 ,
,
то определителем третьего порядка называется число:
det A = 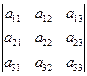 = D = a 11 a 22 a 33 + a 21 a 32 a 13 + a 31 a 12 a 23 - a 31 a 22 a 13 - a 21 a 12 a 33 - a 11 a 32 a 23 (17)
= D = a 11 a 22 a 33 + a 21 a 32 a 13 + a 31 a 12 a 23 - a 31 a 22 a 13 - a 21 a 12 a 33 - a 11 a 32 a 23 (17)
На практике для вычисления определителя третьего порядка пользуются следующей теоремой разложения (которая приводится здесь без доказательства).
Теорема 3. Определитель третьего порядка равен сумме парных элементов любого ряда (т.е. любой строки или любого столбца матрицы) на их алгебраические дополнения.
Так в соответствии с данной теоремой:
D = a 11 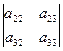 (-1)1+1 + a 21
(-1)1+1 + a 21 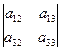 (-1)2+1 + a 31
(-1)2+1 + a 31 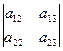 (-1)3+1 - (разложение по 1-му столбцу);
(-1)3+1 - (разложение по 1-му столбцу);
D = a 21 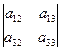 (-1)2+1 + a 22
(-1)2+1 + a 22 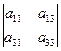 (-1)2+2 + a 23
(-1)2+2 + a 23 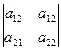 (-1)2+3 - (разложение по 2-ой строке).
(-1)2+3 - (разложение по 2-ой строке).
И так далее …
Литература
1. Б.П. Демидович и И.А. Марон. Основы вычислительной математики. – М.: Наука, 1970. – 664 с.
2. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002.- 840 с.
3. В.А. Ильин, Э.Г. Позняк. Линейная алгебра. – М.: Наука, 1974.- 296 с.
Дата публикования: 2015-09-17; Прочитано: 337 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
