Примеры решения типовых задач. Пример 1. Рассмотрим задачу о стационарном распределении тепла в плоской изолированной пластине со стороной 1

Пример 1. Рассмотрим задачу о стационарном распределении тепла в плоской изолированной пластине со стороной 1, если на границе пластины поддерживается постоянная температура (указанная на рис. 6) и если известно, что при заданных краевых условиях, функция u (x, y), описывающая распределение температуры в пластине, является решением уравнения Лапласа:

.

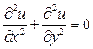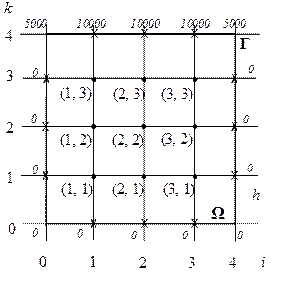
Рисунок 7 – расчётная область с граничными условиями для примера 1

Решение. Для решения задачи построим сетку с шагом 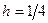. При этом получим девять внутренних узлов (на рис. 6 обозначены точками), в которых необходимо определить значения функции u (x, y). Построенная сеточная область также имеет 12 граничных узлов (на рис. 7 обозначены крестиком), которые лежат на границе Г расчётной области, поэтому значения искомой функции в них определяются из граничных условий.

Далее для полученных внутренних узлов сетки необходимо записать конечно-разностные уравнения для искомой функции u_{i , k} i = 1, 2, 3; k = 1, 2, 3. Однако на данной сетке (как видно из рисунка 7), в силу симметрии граничных условий для значений искомой функции выполняются равенства:

u ₁₁ = u ₃₁; u ₁₂ = u ₃₂; u ₁₃ = u ₃₃; (22)

Это сокращает количество неизвестных значений функции u (x, y) во внутренних узлах до шести. Таким образом, в узлах (3, 1), (3, 2), (3, 3) конечно-разностные уравнения писать нет необходимости.

В остальных шести внутренних узлах (1, 1), (2, 1), (1, 2), (2, 2), (1, 3), (2, 3) в соответствии с соотношением (10):

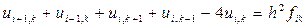
при 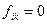получаем соответственно шесть уравнений:

(23)

В эти уравнения входят ещё 12 значений функции в граничных точках сетки. И поскольку граничные точки лежат на Г, то значения функции u (x, y) в них мы берём из краевых условий:

(24)

Заметим, что в остальных узлах краевые условия не используются.

Далее учитывая соотношения (22) и (23) из (24) получаем систему уравнений для определения неизвестных значений функции u (x, y) во внутренних узлах:

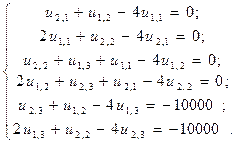(25)

Решив систему (25) методом Гаусса, окончательно получаем

Ответ: u ₁₁ = 714; u ₂₁ = 982; u ₁₂ = 1875; u ₂₂ = 2500; u ₁₃ = 4286; u ₂₃ = 5268.

Пример 2. Из теории упругости известно, что задача об упругой деформации квадратной пластины под действием постоянной силы сводится к решению уравнения Пуассона:

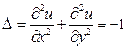
с нулевыми краевыми значениями. Найти решение этой задачи методом сеток, приняв сторону квадрата равной 1 и шаг h сетки равным .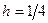

Решение. В данном случае имеет место полная симметрия значений искомой функции, так как все краевые условия краевые, а функция f (x, y) постоянна (рис. 8).

Поэтому конечноразностные уравнения достаточно составить для четверти квадрата, т.е. для узлов (1, 1), (2, 1), (1, 2), (2, 2).

Рисунок 8 – расчётная область с нулевыми граничными условиями для примера 2

В указанных четырёх узлах (1, 1), (2, 1), (1, 2), (2, 2), в соответствии с соотношением (10):

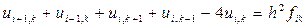
которое для данной задачи имеет вид:

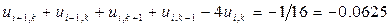
получаем соответственно систему уравнений:

(26)

Далее, учитывая нулевые граничные условия:

и что в силу симметрии задачи относительно центра пластины - узел (2, 2):

u ₁₁ = u ₃₁ = u ₁₃ = u ₃₃; и u ₁₂ = u ₃₂ = u ₂₃ = u ₂₁

систему (26) перепишем в виде:

(27)

поскольку u ₁₂ = u ₂₁, то второе и третье уравнения последней системы совпадают, поэтому вместо неё окончательно имеем систему трёх уравнений:

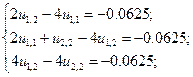(28)

Решив эту систему получаем

Ответ: u ₁₁ = 0,0429; u ₁₂ = u ₂₁ = 0,0547; u ₂₂ = 0,0703.

Пример 3. Решение краевых задач для криволинейных областей.

Найти приближённое решение уравнения:

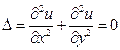, (29)

удовлетворяющее на окружности 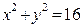условию:

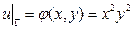(30)

Решение. В данном случае границей Г расчётной области является окружность радиуса R = 4, с центром в начале координат. В соответствии с (30) функция j (x, y), задающая значения искомого решения u (x, y) на этой окружности, симметрична относительно начала координат (рис. 9 а), поэтому, достаточно найти решение данной краевой задачи на четверти круга.

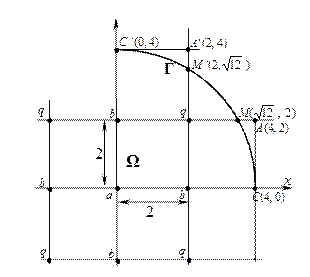
Рисунок 9а. Рисунок 9б.

Будем решать данную задачу поэтапно.

1) На первом этапе возьмём крупную сетку с шагом h = 2 (рис. 9 б) и найдём значения координат точек пересечения линий сетки с окружностью (на рис. 9 б указанные точки пресечения обозначены соответственно как М и М' ).

Поскольку точки М и М' являются точками пересечения окружности и линий сетки, имеющих соответственно уравнения y = 2 и x = 2, то их координаты можно найти решая соответственно системы уравнений:

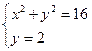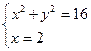(31) (32)

Из (31) и (32) соответственно получаем, что точки М и М' имеют координаты:

М : x = 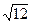, y = 2 и М' : x = 2, y = .

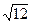Зная координаты точек М и М' в соответствии с граничным условием (30) определяем значения решения в точках М и М'.

u ( М ) = 12×4 = 48; u ( М' ) = 4×12 = 48.

Для аппроксимации значений искомой функции u (x, y) в граничных узлах сетки А (4, 2) и А' (2, 4) сносим значения решения из точек М и М' границы Г в точки А (4, 2) и А' (2, 4), т.е. полагаем:

u (A)» u ( М ) = 48; и u (A' )» u ( М' ) = 48.

Для граничных узлов С (4, 0) и С' (0, 4), лежащих на границе расчётной области Г, очевидно имеем:

u (С) = u (С' ) = 0;

Значения искомого решения u (x, y) во внутренних узлах сетки, которые обозначены на рис. (рис. 9 б) буквами a, b, c находим из разностного уравнения:

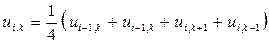(11)

u (a) = ;

u (b) = ;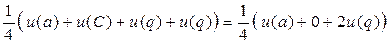

u (q) = .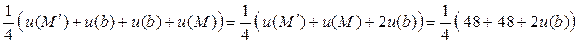

записывая последние равенства более компактно, имеем систему уравнений:

(33)

Решая систему уравнений (33) находим:

u (a) = 24; u (b) = 24; u (c) = 36.

2) На втором этапе возьмём более мелкую сетку с шагом h = 1 и «грубо» аппроксимируем граничные значения посредством переноса значений с границы области Г в граничные узлы сетки (рис. 9 в).

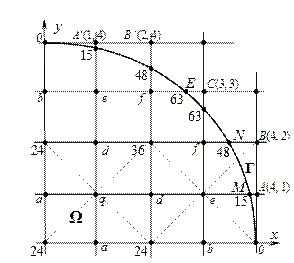
Рисунок 9 в.

Как и на первом этапе координаты точек пересечения этой сетки с окружностью определяются из следующих систем уравнений:

; ; ; ; ; ;

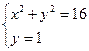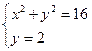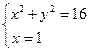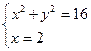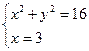Решая данные системы уравнений, получаем соответственно следующие значения координат точек пересечения линий мелкой сетки и границы Г расчётной области:

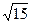(, 1); (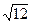, 2); (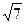, 3); (1, 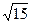); (2, 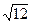); (3, );

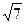Отсюда в соответствии с граничным условием (30) получаем, что значения искомой функции в точках пересечения линий сетки и границы Г соответственно равны:

15; 48; 63; 15; 48; 63.

Снесём данные значения с границы Г в ближайшие граничные узлы А, А', В, В' и С мелкой сетки, в результате будем иметь:

u (А) = u (А' ) = 15; u (А') = u (В' ) = 48; u (С) = 63;

На рис. 9 в цифрами узлах сетки обозначены значения искомой функции
u (x, y), вычисленные на предыдущем этапе по крупной сетке, и значения, которые найдены в точках пересечения мелкой сетки и границы Г из граничного условия (30).

Далее используя указанные значения функции u (x, y) найденные на первом этапе в узлах крупной сетки с шагом h = 2 и значения в граничных узлах мелкой сетки, а также учитывая симметрию задачи по формулам:

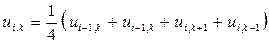(11)

(14)

составляем соответственно конечно-разностные уравнения для значений искомой функции u (x, y) в узлах a, b, d, f и q, e:

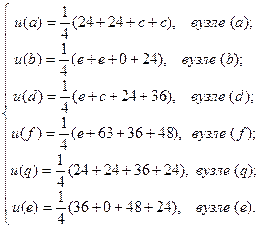(34)

Отметим, что при составлении конечно-разностных уравнений системы (34) для узлов a, b, d, f и q, e использовались шаблоны с разной связью узлов. Решая далее систему уравнений (34) приближённо находим:

u (a) = 26; u (b) = 20; u (q) = 27, u (d) = 28; u (e) = 27; u (f) = 44.

3) На третьем этапе уточняем (аппроксимируем) значения искомой функции u (x, y) в граничных узлах А, А', В, В' и С используя формулу (17).

Для узла А формула (17) перепишется в виде: u_A =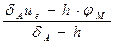

где d_А = 4 - 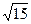» 0.13; h = 1, u (e) = 27; j_M = 15; в результате имеем:

u_A =

Для узла В формула (17) перепишется в виде: u_В =

где d_В = 4 - 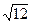» 0.54; h = 1, u ( f) = 44; j _N = 48; в результате имеем:

u_B =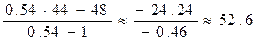

Для узла С формула (17) перепишется в виде: u_С =

где d_Е = 3 - 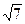» 0.35; h = 1, u ( f) = 44; j _Е = 63; в результате имеем:

u_С =

Таким образом, в граничных узлах имеем: u_A = 13; u_B = 52.6; u_С = 73.2;

Заключение (план - аннотация лекции №28).

В лекции рассмотрена идея метода сеток, или метода конечных разностей, который является одним из распространённых методов численного решения уравнений с частными производными. В основе метода сеток лежит идея замены фигурирующих в уравнении математической физики частных производных конечно-разностными отношениями различной степени точности.

Подробно изложена методика использования метода сеток для решения краевых задач для уравнений эллиптического типа, рассмотрены различные варианты связи узлов в «крестообразных» шаблонах прямоугольных сеток. Приведена оценка погрешности разностного метода решения задачи Дирихле.

Рассмотрена идея аппроксимации граничных условий для решения задачи Дирихле в случае, когда не все граничные узлы сетки лежат на границе расчётной области, в том числе и для случаев построения сеток с «перекрытием» расчётных областей.

На примере третьей краевой задачи для уравнений эллиптического типа обсуждаются подходы, используемые при аппроксимации граничных условий для других граничных условий, встречающихся при решении краевых задач для эллиптического дифференциального уравнения второго порядка.

Приведены примеры решения типовых задач для уравнений эллиптического типа как для случая прямоугольных, так и для случая криволинейных расчётных областей.

Литература:

1. И.С. Березин, Н.П. Жидков. Методы вычислений. Т. 2. – М.: Физматгиз, 1962. – 620 с.

2. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002. – 840 стр.

3. В.Ф. Формалёв, Д.Л. Ревизников. Численные методы. – М.: Физматлит, 2004. 400 с.

4. Б.П. Демидович, И.А. Марон, Э.З. Шувалова. Численные методы анализа.
– М.: Наука, 1967. – 368 с.

5. Н.В. Копчёнова, И.А. Марон. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 368 с.