Пример решения краевой задачи методом конечных разностей

Пример 1. Методом конечных разностей найти решение краевой задачи:

y ²(x) + (1 + x ²) y (x) = -1. (41)

y (-1) = 0; (42)

y (1) = 0. (43)

Механически данная краевая задача описывает прогиб некоторого бруса, концы которого шарнирно закреплены симметрично от начала координат в точках x = -1,
x = 1, т.е. y (x) описывает координату прогиба стержня на участке [-1, 1] оси x (рис. 2).

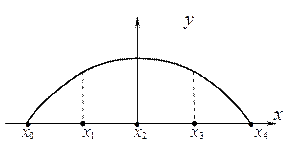
Рисунок 2 – Профиль изгиба бруска.

Для грубого решения задачи выберем шаг сетки h = тогда выбирая начало отсчёта на левом конце бруска, решение данной задачи ищем на сетке:

x ₀ = -1; x ₁ = ; x ₂ = 0; x ₃ = ; x ₄ = 1;

Сравнивая данное дифференциальное уравнение (41):

y ²(x) + (1 + x ²) y (x) = -1

с видом ДУ (2), используемым при формулировке краевой задачи (2) – (4):

y ¢¢(x) + p (x) y¢ (x) + q (x) y (x) = f (x), x Î [ a, b ],

заключаем, что для данной краевой задачи функции p (x), q (x) и f (x), имеют вид:

p (x) = 0, q (x) = 1 + x ², f (x) = - 1.

Для решения данной краевой задачи методом конечных разностей уравнение (41) заменяется во внутренних узлах сетки разностным уравнением (35):

, i = 1, 2, 3;

а функции p (x), q (x) и f (x) заменяются соответствующими сеточными значениями:

p_i = p (x_i) = 0, q_i = q (x_i) = 1 + (x_i)², f _i = f (x_i) = - 1.

поэтому для данного случая разностное уравнение (35) перепишется в виде:

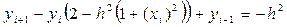, i = 1, 2, 3. (44)

В данном случае мы имеем дело с краевой задачей первого рода, т.е. со случаем, когда краевые условия (42), (43) не содержат значений первой производной, т.е. в данном случае при стандартной записи краевых условий в виде (3), (4) имеем:

y (-1) = 0 Û a₀ y (a) + a₁ y ¢(a) = A Þ a = -1; a₀ = 1; a₁ = 0; A = 0;

y (1) = 0 Û b₀ y (b) + b₁ y ¢(b) = B Þ b = 1; b₀ = 1; b₁ = 0; B = 0;

поэтому окончательно краевые условия можно переписать в виде:

y (x ₀) = y ₀ = 0; (45)

y (x_n) = y (x ₄) = y ₄ = 0; (46)

Таким образом, из (44) - (46) для решения краевой задачи (41) – (43) окончательно имеем систему уравнений:

y ₀ = 0; i = 0;

, i = 1; x ₁ = ;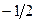

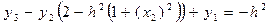, i = 2; x ₂ = 0;

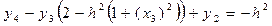, i = 3; x ₃ = ;

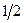y ₄ = 0; i = 4;

Далее отметим, что в силу симметрии данной задачи (брусок прогибается симметрично относительно начала координат) заключаем, что y ₃ = y ₁, поэтому, рассматривая второе и третье уравнение последней системы, имеем:

;

;

отсюда при x ₂ = 0; h = 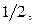x ₁ = 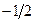; y ₀ = 0 имеем:

;

;

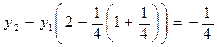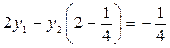или

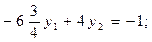
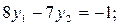
откуда y ₂ = 0.967; y ₁ = 0.721;

Таким образом, окончательно имеем: y ₀ = 0; y ₁ = 0.721; y ₂ = 0.967; y ₃ = 0.721; y ₄ = 0.

Замечание. При рассмотрении метода конечных разностей в § 4 данной лекции для решения краевой задачи (2) – (4) было предложено две системы уравнений:

- первая система - уравнения (35), (37), (38);

- вторая система - уравнения (35), (39), (40);

Данные системы отличаются друг от друга формулами аппроксимации производной первого порядка в краевых условиях (2) – (4), т.е. в первой системе производные в краевых условиях аппрксимировались разностными отношениями первого порядка точности, а во второй системе разностными отношениями второго порядка точности.

Поскольку в данном примере (о профиле изгиба бруска) имеют место краевые условия первого рода, которые не содержат значений первой производной на границах отрезка, то для данного случая алгоритмы решения краевой задачи на основе первой и второй систем совпадают.

Заключение (план - аннотация лекции №25).

В лекции 8 рассмотрена общая постановка краевой задачи для обыкновенных дифференциальных уравнений второго порядка. Дано описание краевых условий различного типа. Приведена классификация методов решения краевых задач.

В качестве методов сведения краевых задач к начальным - к задачам Коши - рассмотрены:

- метод «пристрелки»;

- метод редукции;

- метод дифференциальной прогонки.

Рассмотрен один из универсальных методов решения краевых задач, основанный на простейших аппроксимаций производных в узлах сетки разностными отношениями первого и второго порядка точности - метод конечных разностей.

Приведен пример решения краевой задачи методом конечных разностей.

Литература:

1. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002. – 840 стр.

2. Б.П. Демидович, И.А. Марон, Э.З. Шувалова. Численные методы анализа.
– М.: Наука, 1967. – 368 с.

3. В.Ф. Формалёв, Д.Л. Ревизников. Численные методы. – М.: Физматлит, 2004. 400 с.