Семейство методов Рунге-Кутта

Исправленный метод Эйлера (13) и другие методы, основанные на пошаговом представлении решения y (x) задачи Коши (1),(2) рядом Тейлора, требуют последовательного дифференцирования уравнения (1) для получения тейлоровских коэффициентов (которыми являются производные различных порядков от решения y (x)). Это приводит к необходимости вычисления на каждом шаге частных производных от неявной функции f (x, y). Это является одним из недостатков таких методов.

В этой связи привлекательной является идея построения методов Рунге-Кутта, которые хотя и основаны на разложении искомого решения y (x) в ряд Тейлора, но не требуют вычисления частных производных неявной функции f (x, y).

Пусть известно разложение по формуле Тейлора для искомого решения y (x_{i+ 1}) в окрестности точки x_i:

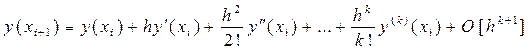(14)

Перепишем это выражение в виде:

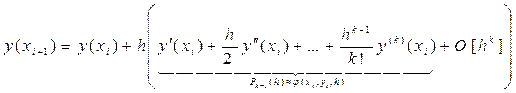(15)

Полином 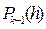в правой части формулы (15) представляет собой фрагмент исходного ряда Тейлора (14), содержащий значения производных y ¢(x_i), y ¢¢(x_i),…, y ^{( k )}(x_i) искомого решения в точке x_i.

Идея Рунге метода Рунге – Кутта [2, стр.116] состоит в том, чтобы, используя метод неопределённых коэффициентов, аппроксимировать (с тем же порядком точности 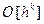) данный полином:

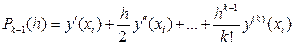(16)

некоторой функцией j (x, y, h), не содержащей частных производных от функции
f (x, y). В результате чего формулу (15) можно будет переписать в виде:

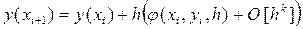
(17)

Метод Рунге-Кутта первого порядка.

Если искомое решение y (x_{i+ 1}) представить рядом Тейлора первого порядка по h т.е. с точностью до слагаемых линейных по h:

,

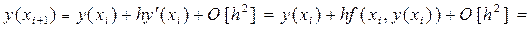
то в соответствии с идеей метода Рунге-Кутта в качестве функции j (x_i, y_i, h), аппроксимирующей с порядком точности 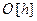фрагмент ряда Тейлора 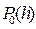следует выбрать функцию j (x_i, y_i, h) = f (x_i, y_i).

Таким образом, при представлении решения y (x_{i+ 1}) рядом Тейлора первого порядка (случай k = 1) определяющее метод Рунге-Кутта выражение (17) превращается в формулу Эйлера:

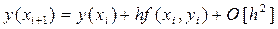
И, следовательно, можно считать, что метод Эйлера является простейшим примером метода Рунге-Кутта первого порядка.

Метод Рунге-Кутта второго порядка.

Метод Рунге-Кутта второго порядка соответствует случаю, когда искомое решение y (x_{i+ 1}) представляется рядом Тейлора с точностью до слагаемых второго порядка по h:

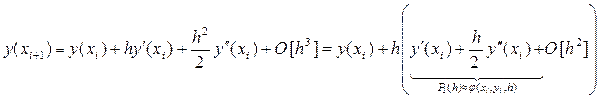(18)

В этом случае соотношение (17), определяющее метод Рунге-Кутта, имеет вид:

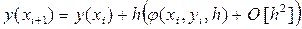(19)

Поэтому в соответствии с идеей метода Рунге-Кутта параметры функции j (x, y, h) подбирают, из условия, что она должна аппроксимировать с точностью до слагаемых линейных по h полином:

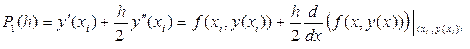(20)

Для того, чтобы определить вид функции j (x, y, h), аппроксимирующей полином (20), перепишем аппроксимируемый полином 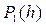в несколько ином виде.

Если для аппроксимации производной 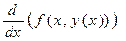, входящей в правую часть выражения (20) использовать разностное отношение общего вида:

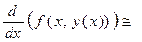
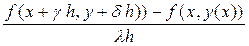
где l, g и d - некоторые пока неизвестные параметры, то аппроксимируемый полином (20) можно переписать в виде:

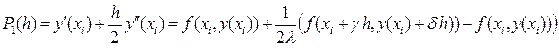(21)

Отсюда ясно, что функцию j (x_i, y_i, h) аппроксимирующую полином (21) можно взять в виде выражения:

j (x_i, y_i, h) = b f (x_i, y (x_i)) + a f (x_i +g h, y (x_i) + d h). (22)

Здесь b, a, g и d - неизвестные параметры, значения которых нужно определить.

В результате с учётом вида функции j (x_i, y_i, h), определяемой выражением (22), формула (18), определяющая метод Рунге-Кутта второго порядка, может быть переписана в виде:

y (x_{i+ 1}) = y (x_i) + h ×( b f (x_i, y (x_i)) + a f (x_i +g h, y (x_i) + d h) + 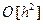) (23)

Поскольку функция j (x_i, y_i, h) (22) должна аппроксимировать полином (20), содержащий линейные слагаемые по h, то функцию f ( x_i +g h, y (x_i) + d h ) из выражения (22) раскладывают в ряд Тейлора с точностью до линейных по h слагаемых:

f (x_i +g h, y (x_i) + d h) = f (x_i, y (x_i) ) + g h f¢_x (x, y (x)) 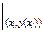+ d h f¢_y (x, y (x)) 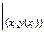+ 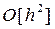(24)*

(* Схема разложения функции двух переменных в ряд Тейлора [3, стр. 266] приведена для справок в приложении к данной лекции).

Подставляя разложение (24) в формулу (23) получим следующую формулу для выражения метода Рунге-Кутта второго порядка:

y (x_{i+ 1}) = y (x_i) + h (b + a) f (x_i, y (x_i)) + a h ²(g f¢_x (x, y (x)) 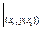+ d f¢_y (x, y (x)) 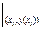) + 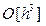(25)

Далее неизвестные параметры b, a, g и d, в формуле (25), определяют так, чтобы представляемое формулой (25) разложение решения y (x_{i+ 1}) с тем же порядком 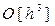аппроксимировало разложение (18) решения y (x_{i+ 1}) в ряд Тейлора:

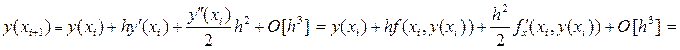
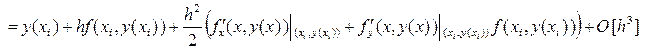(26)

Приравнивая в формулах (25) и (26) коэффициенты в главных порядках по h найдём, что параметры b, a, g и d, определяющие функцию j (x_i, y_i, h) (22) должны удовлетворять следующей совокупности условий:

(b + a) = 1; a g = 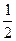; a d = 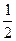f (x_i, y (x_i)); Û 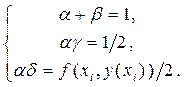(27)

Полученная система уравнений (27) содержит три уравнения относительно четырёх параметров b, a, g и d. Это свидетельствует о наличии одного свободного параметра, через который можно выразить остальные параметры.

Выражая из (27) параметры b, g и d через параметр a получим:

b = 1 - a, g = 1/2 a и d = f (x_i, y (x_i)) (28)

В результате подстановки этих значений параметров в формулу (23) приходим к однопараметрическому семейству методов Рунге - Кутта второго порядка.

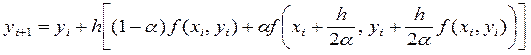(29)

где a (0 < a £ 1) является параметром семейства методов решения задачи Коши.

Схема реализации методов Рунге-Кутта второго порядка.

При реализации вычислительного процесса на ЭВМ любой метод из семейства методов Рунге-Кутта второго порядка (29) реализуют по следующей схеме.

1. На каждом шаге, т.е. при каждом i = 0,1, 2, …, вычисляют значения функций: h i 1 = f (xi, y (xi)), h i 2 = 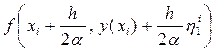. 2. Затем находят шаговую поправку D y (xi) = h [(1 - a) h i 1 + a) h i 2], прибавление которой к результату предыдущего шага даёт приближённое значение решения y (x) в точке xi +1 = xi + h: y (xi +1) = y (xi) + D yi. Методы такой структуры называют двухэтапным по количеству вычислений значений функции (т.е. правой части дифференциального уравнения (1)) на одном шаге.

(30)

Частные случаи методов Рунге-Кутта второго порядка.

Выделим из семейства методов (29) два наиболее простых частных случая, соответствующих значениям a = 1 и a = 1/2.

1.) При a = 1 семейство методов Рунге-Кутта (29) приобретает наиболее простой вид, который называется методом средней точки:

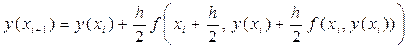(31)

Поясним на рис. 1 графически смысл метода средней точки.

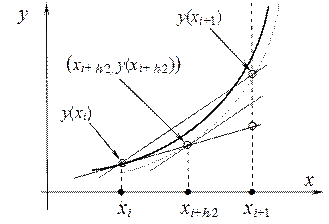
Рисунок 1 – Геометрическая иллюстрация метода Рунге-Кутта второго порядка

Сначала через точку x_i проводим касательную, наклон которой определяем из исходного уравнения:

y (x) = y (x_i) + f (x_i, y (x_i))(x - x_i) (32)

Далее делаем половинный шаг по схеме ломанных, т.е. находим значение данной касательной (32) в точке x_{i+h/ 2}:

y (x_{i+h/ 2}) = y (x_i) + 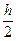f (x_i, y (x_i)) (33)

Затем из дифференциального уравнения (1) определяем наклон интегральной кривой y ¢(x) в данной точке (x_{i+h/ 2}, y (x_{i+h/ 2})), т.е. находим чему был бы равен наклон интегральной кривой y ¢(x), если бы она проходила через точку (x_{i+h/ 2}, y (x_{i+h/ 2})):

y ¢(x_{i+h/ 2}) = f (x_{i+h/ 2}, y (x_i) + 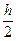f (x_i, y (x_i))) (34)

По этому наклону (34) и определяем окончательно приращение искомого решения y (x_i) на целом шаге h:

y (x_{i +1}) - y (x_i) = h y ¢(x_{i+h/ 2}) = h f (x_{i+h/ 2}, y (x_i) + 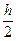f (x_i, y (x_i))) (35)

2.) При a = 1/2 формула (29) превращается в рассмотренный ранее метод Хьюна:

, (i = 0,1, …, n),

Замечания.

1. Выбрать параметр a так чтобы схема (29) давала бы аппроксимацию третьего порядка невозможно.

2. Приведём без доказательства теорему о сходимости и точности методов Рунге-Кутта второго порядка.

Теорема. Если функция f (x, y (x)) непрерывна и ограничена вместе со своими вторыми производными, то решение, полученное по схеме (29), равномерно сходится к точному решению с погрешностью 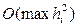, т.е. данный метод Рунге-Кутта имеет второй порядок точности.