 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вычисление криволинейного интеграла первого рода с помощью определенного интеграла
|
|
Простая кривая  заданная уравнениями (1), называется гладкой (кусочно гладкой), если функции
заданная уравнениями (1), называется гладкой (кусочно гладкой), если функции  и
и 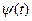 имеют непрерывные (кусочно непрерывные) производные, одновременно не обращающиеся в нуль на
имеют непрерывные (кусочно непрерывные) производные, одновременно не обращающиеся в нуль на 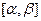 (на
(на 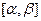 , за исключением конечного числа точек).
, за исключением конечного числа точек).
Теорема 5. Если  - кусочно гладкая кривая, заданная уравнения (1), и функция
- кусочно гладкая кривая, заданная уравнения (1), и функция  кусочно непрерывна вдоль кривой
кусочно непрерывна вдоль кривой  , то существует криволинейный интеграл (2) и справедливо равенство
, то существует криволинейный интеграл (2) и справедливо равенство
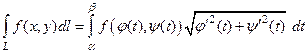 . (3)
. (3)
Замечание 5. Предположим, что  непрерывна вдоль кривой
непрерывна вдоль кривой  . Тогда имеют место следующие утверждения.
. Тогда имеют место следующие утверждения.
1. Если кривая  задана уравнением
задана уравнением 
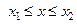 , и
, и  имеет непрерывную производную на
имеет непрерывную производную на 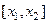 , то существует интеграл (2) и справедливо равенство
, то существует интеграл (2) и справедливо равенство
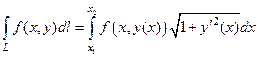 . (4)
. (4)
2. Если кривая  задана в полярных координатах уравнением
задана в полярных координатах уравнением 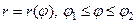 , и
, и 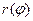 имеет непрерывную производную на
имеет непрерывную производную на  , то существует интеграл (2) и имеет место равенство
, то существует интеграл (2) и имеет место равенство
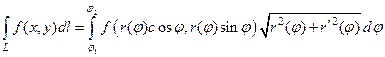 (5)
(5)
3. Для гладкой пространственной кривой, заданной параметрически уравнениями
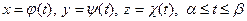 ,
,
справедлива формула
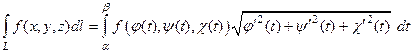 (6)
(6)
Основные свойства криволинейного интеграла первого рода:
1) Криволинейный интеграл первого рода не зависит от направления пути интегрирования:
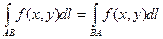 .
.
2) 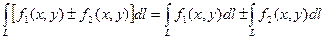 .
.
3) 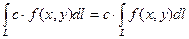 , где
, где 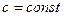 .
.
4) Если контур интегрирования  разбит на две части
разбит на две части 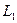 и
и 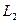 , то
, то
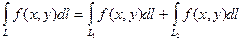 .
.
Дата публикования: 2015-09-17; Прочитано: 325 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
