 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Поверхностный интеграл II рода
|
|
Пусть задана гладкая поверхность 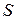 . Сторона поверхности
. Сторона поверхности 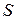 , в каждой точки которой построен вектор нормали
, в каждой точки которой построен вектор нормали  , называется положительной, а другая ее сторона (если она существует) – отрицательной. Если, в частности, поверхность
, называется положительной, а другая ее сторона (если она существует) – отрицательной. Если, в частности, поверхность 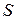 является замкнутой и ограничивает некоторую область пространства
является замкнутой и ограничивает некоторую область пространства  , то положительной или внешней сторонойповерхности называется та ее сторона, нормальные векторы которой направлены от области
, то положительной или внешней сторонойповерхности называется та ее сторона, нормальные векторы которой направлены от области  , а отрицательной или внутренней – сторона, нормальные векторы которой направлены в область
, а отрицательной или внутренней – сторона, нормальные векторы которой направлены в область  .
.
Поверхность, у которой существует положительная (внешняя) и отрицательная (внутренняя) стороны, называется двухсторонней. Примерами двухсторонних поверхностей являются плоскость, поверхности второго порядка, тор и др. Двухсторонняя поверхность характеризуется следующим свойством: если основание вектора нормали  непрерывно перемещать по любому замкнутому контуру
непрерывно перемещать по любому замкнутому контуру 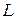 , лежащему на такой поверхности, то при возвращении в исходную точку направление
, лежащему на такой поверхности, то при возвращении в исходную точку направление  совпадает с исходным.
совпадает с исходным.
Для односторонних поверхностей указанное перемещение нормали  при возвращении в исходную точку приводит к «антинормали», т.е. к вектору
при возвращении в исходную точку приводит к «антинормали», т.е. к вектору  . Классическим примером односторонней поверхности является лист Мебиуса.
. Классическим примером односторонней поверхности является лист Мебиуса.
Поверхность 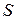 с выбранной стороной называется ориентированной.
с выбранной стороной называется ориентированной.
Пусть в прямоугольной системе координат  задана некоторая область
задана некоторая область  . И пусть в этой области задана поверхность
. И пусть в этой области задана поверхность 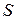 , ограниченная некоторой пространственной линией
, ограниченная некоторой пространственной линией 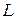 .
.
Относительно поверхности 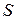 будем предполагать, что в каждой ее точке
будем предполагать, что в каждой ее точке 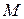 определяется положительное направление нормали единичным вектором
определяется положительное направление нормали единичным вектором  , направляющие косинусы которого являются непрерывными функциями координат точек поверхности.
, направляющие косинусы которого являются непрерывными функциями координат точек поверхности.
Если поверхность 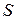 задана уравнением
задана уравнением  , то нормальный вектор
, то нормальный вектор  , образующий с осью
, образующий с осью  острый угол
острый угол 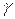 , определяется следующим образом:
, определяется следующим образом: 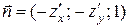 , тогда координаты единичного вектора нормали
, тогда координаты единичного вектора нормали  :
:
 .
.
Если поверхность 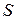 задана уравнением
задана уравнением 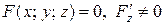 ,
, 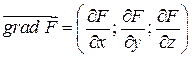 , то
, то
 ,
,
где знак «+» берется в случае, когда угол 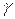 - острый, а знак «-» в случае, когда
- острый, а знак «-» в случае, когда 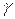 - тупой.
- тупой.
Пусть в области  пространства
пространства  определена вектор-функция
определена вектор-функция
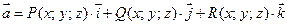 ,
,
где 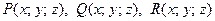 - функции непрерывные в области
- функции непрерывные в области  .
.
Разобьем поверхность 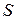 на элементарные площадки
на элементарные площадки 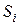 , площадки которых
, площадки которых  , а диаметры – через
, а диаметры – через 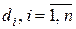 . На каждой площадке
. На каждой площадке 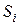 выберем произвольную точку
выберем произвольную точку 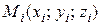 . Найдем интегральную сумму
. Найдем интегральную сумму 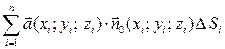 .
.
Предел интегральной суммы, найденный при условии, что 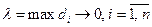 ,
, 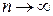 , называется поверхностным интегралом второго рода от вектор-функции
, называется поверхностным интегралом второго рода от вектор-функции 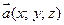 по поверхности
по поверхности 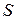 и обозначается
и обозначается 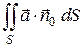 .
.
Таким образом, по определению
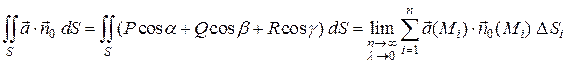 .
.
(3.3)
Надо отметить, что если поверхность 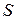 такова, что в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки
такова, что в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки 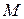 по поверхности, и если вектор-функция
по поверхности, и если вектор-функция 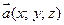 непрерывна на этой поверхности, то этот предел существует.
непрерывна на этой поверхности, то этот предел существует.
Произведение 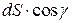 есть проекция площадки
есть проекция площадки 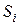 на плоскость
на плоскость 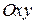 , то
, то  . Аналогично получаем:
. Аналогично получаем: 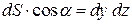 ,
,  . Тогда формулу (3.3) можно записать в виде
. Тогда формулу (3.3) можно записать в виде
 . (3.4)
. (3.4)
Каждое слагаемое интегральной суммы 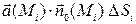 может быть истолковано механически следующим образом: это произведение равно объему цилиндра с основанием
может быть истолковано механически следующим образом: это произведение равно объему цилиндра с основанием  и высотой
и высотой  . Если вектор
. Если вектор 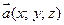 есть скорость жидкости, протекающей через поверхность
есть скорость жидкости, протекающей через поверхность 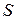 , то произведение
, то произведение 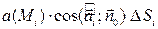 равно количеству жидкости, протекающей через площадку
равно количеству жидкости, протекающей через площадку  за единицу времени в направлении вектора
за единицу времени в направлении вектора  .
.
Выражение 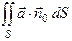 представляет собой общее количество жидкости, протекающей в единицу времени через поверхность
представляет собой общее количество жидкости, протекающей в единицу времени через поверхность 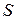 в положительном направлении, если под вектором
в положительном направлении, если под вектором 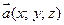 подразумевать вектор скорости течения жидкости в данной точке. Поэтому поверхностный интеграл второго рода называется потоком векторного поля
подразумевать вектор скорости течения жидкости в данной точке. Поэтому поверхностный интеграл второго рода называется потоком векторного поля 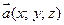 через поверхность
через поверхность 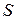 .
.
Отметим, что если 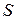 - замкнутая поверхность, то поверхностный интеграл по внешней стороне ее обозначается
- замкнутая поверхность, то поверхностный интеграл по внешней стороне ее обозначается 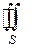 , по внутренней -
, по внутренней - 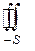 .
.
Дата публикования: 2015-07-22; Прочитано: 233 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
