Устойчивость по Ляпунову положений равновесия

Практическое занятие №3

Устойчивость системы. Линеаризация уравнений. Устойчивость по Ляпунову.

Устойчивость по Ляпунову положений равновесия

Пусть в области евклидова пространства 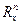задана автономная система уравнений

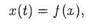
где 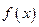— непрерывно дифференцируемая в , вектор-функция с n компонентами, и пусть 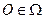, является положением равновесия автономной системы Разложим 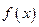в окрестности х =0 по формуле Тейлора с остаточным членом в форме Пеано

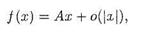
где матрица

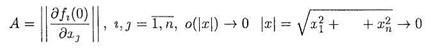
Линейная автономная система

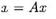
называется линеаризацией системы x(t) = f(x) в точке х = 0 или системой первого приближения для x(t) = f(x)

Из теорем Ляпунова следует, что в случае, когда все собственные значения А имеют отрицательные вещественные части, х = 0 является асимптотически устойчивым положением равновесия для системы 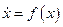Eслu же хотя бы одно собственное значение А имеет положительную вещественную часть, то х = 0 является неустойчивым положением равновесия для системы 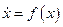Для линейной автономной системы 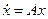эти результаты можно уточнить

Пример 1 Исследовать устойчивость положений равновесия с помощью системы первого приближения автономной системы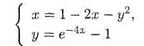

Найдем сначала положения равновесия системы Для этого необходимо решить систему уравнений

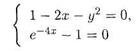
Получаем два положения равновесия (0,1) и (0,-1)

Исследуем устойчивость положения равновесия (0,1) С этой целью в автономной системе сделаем замену 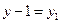и правые части полученной системы разложим по формуле Тейлора в окрестности точки (0,0), являющейся положением равновесия новой системы

Имеем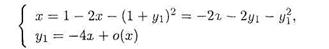

Матрица

имеет собственные значения 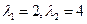Следовательно, положение равновесия (0,1) является неустойчивым

Для исследования устойчивости второго положения равновесия (0, —1) в заданной системе сделаем замену у +1 = у\ Тогда точка (0,-1) перейдет в точку (0,0) и можно в окрестности (0,0) разложить по формуле Тейлора правые части новой системы Получаем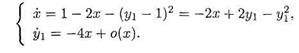

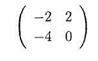
Матрица имеет собственные значения 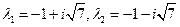Следовательно, положение равновесия (0,-1) является асимптотически устойчивым. В тех случаях, когда вещественные части всех собственных значений матрицы А неположительны, причем хотя бы одно собственное значение А имеет вещественную часть равную нулю, исследование устойчивости положений равновесия нелинейной автономной системы с помощью системы первого приближения, как правило невозможно, так как начинают влиять нелинейные члены. В таких случаях используют метод функций Ляпунова (второй метод Ляпунова).

ПРИМЕР 2. Исследовать устойчивость положений равновесия автономной системы

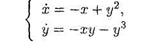
Единственным положением равновесия является точка (0,0) В этом случае матрица

не позволяет воспользоваться теоремой Ляпунова об устойчивости по первому приближению. Применим второй метод Ляпунова. Если взять в качестве функции Ляпунова функцию V(x.y)=х² + у², то ее производная в силу автономной системы

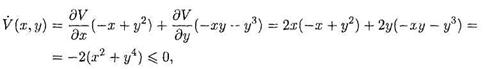
причем V(x,y) = 0 лишь при х = у = 0. По теореме Ляпунова отсюда следует, что точка (0,0) является асимптотически устойчивым положением равновесия системы.

Исследовать устойчивость положений равновесия с помощью системы первого приближения (1—15):

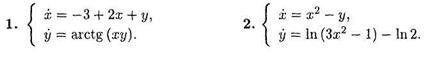
16. При каких значениях вещественного параметра а система

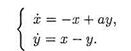
имеет асимптотически устойчивое положение равновесия (0,0)?

17. При каких значениях вещественных параметров а и bсистема

имеет устойчивое по Ляпунову положение равновесия (0,0)?

2.1 Автономные системы дифференциальных уравнений n –го порядка.

Рассмотрим автономную систему Автономной системой дифференциальных уравнений n –го порядка называется система, которая в нормальной форме записывается в виде

В векторной форме автономная система имеет вид x' = F(x) (не зависит от t), где

Название автономная система связано с тем, что поскольку производная x' зависит только от x и не зависит от t, то решение само управляет своим изменением. Автономные системы называют также динамическими системами.

Рассмотрим автономную систему

x' = F(x) с непрерывно дифференцируемой правой частью.

Уравнение x = φ(t) — t ∈ [a, b] — параметрическое уравнение фазовой траектории системы.

Пусть x = φ(t) — решение автономной системы, определенное на отрезке [a, b]. Множество точек x = φ(t), t ∈ [a, b] — кривая в пространстве R_xⁿ. Эту кривую называют фазовой траекторией или просто траекторией системы, а пространство R_xⁿ, в котором расположены фазовые траектории, называют фазовым пространством автономной системы.

Точка a называется положением равновесия (точкой покоя) автономной системы, если F(a) = 0. Равенство x = φ(t), t ∈ [a, b] — параметрические уравнения фазовой траектории.

Интегральная кривая системы изображается в (n + 1) –мерном пространстве R_{x, t}ⁿ⁺¹ и может быть определена уравнениями

Ясно, что соответствующая фазовая траектория — проекция интегральной кривой на пространство R_x.

На рисунке приведено изображение интегральной кривой автономной системы и соответствующей фазовой траектории.

Построим интегральную кривую и фазовую траекторию решения задачи Коши

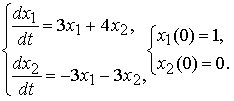
Задачу решим методом исключения:

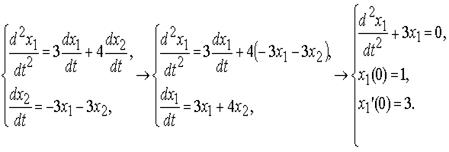
Решим задачи Коши для полученного линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами x₁'' + 3x₁ = 0:

Имеем:

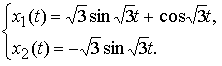
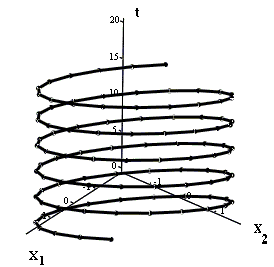
Соответствующая интегральная кривая определяется и пространстве R_x1,x2,t³ уравнениями

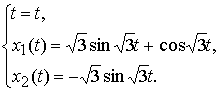
Фазовая кривая, которая является проекцией интегральной кривой на пространство R_x1,x2², определяется уравнениями

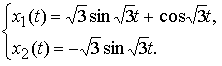
На рисунке приведены изображения интегральной кривой (слева) и соответствующей фазовой кривой (справа).

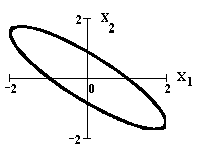
Важнейшим свойством решений автономных систем является следующее:

если вектор–функция x = φ(t) — решение автономной системы, то при любой постоянной C вектор–функция x = φ(t + C) тоже является решением системы.

3 Свойства фазовых траекторий

1. Две фазовые траектории либо не имеют общих точек, либо совпадают.

Это свойство фазовых траекторий означает, что фазовое пространство "расслаивается" на непересекающиеся фазовые траектории.

2. Если a — точка равновесия автономной системы, то x = a — фазовая траектория системы. Положение равновесия называют точкой покоя автономной системы.

3. Фазовая траектория, отличная от точки — гладкая кривая (в каждой точке этой кривой существует ненулевой касательный вектор).

4. Пусть x (t; x(0)) — решение задачи Коши x' = F(x), x(0) = x⁽⁰⁾. Тогда x(t₁ + t₂ ; x⁽⁰⁾) = x(t₂ ; x(t₁ ; x⁽⁰⁾) = x(t₁ ; x(t₂; x⁽⁰⁾) и x(− t; x(t; x⁽⁰⁾)) = x⁽⁰⁾.

Полную информацию о свойствах решений системы дают интегральные кривые..

Более того, некоторые свойства решений ярче проявляются при исследовании фазовых траекторий (фазового пространства системы).

Любую систему дифференциальных уравнений, записанную в нормальной форме, можно свести к автономной системе, увеличив число неизвестных функций на единицу:

Будем полагать, что для рассматриваемых автономных систем выполнены условия теоремы существования и единственности решения задачи Коши.

Таким образом, фазовые траектории системы – это проекции интегральных кривых в пространстве всех трех измерений x, y, t на плоскость x, y (рис.4.3).

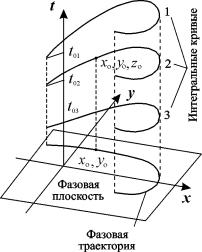Рисунок - фазовые траектории в пространстве

Если условия теоремы Коши выполнены, то через каждую точку пространства x, y, t проходит единственная интегральная кривая. То же справедливо, благодаря автономности, для фазовых траекторий: через каждую точку фазовой плоскости проходит единственная фазовая траектория.

Список использованных источников

1. Н.С. Пискунов Дифференциальное и интегральное исчисления. М.:Интеграл – Пресс, 2001.

2. Дмитриев В.И. Лекции по обыкновенным дифференциальным уравнениям. М.: Изд-во КДУ, 2007.

3. Петровский И.Г. Лекции по теории обыкновенных дифференци­альных уравнений. М.: УРСС, 2003.