Методика вычисления погрешности

На практике любую физическую величину мы имеем возможность измерить ограниченное число раз, поэтому ее истинное значение остается неизменным. За наилучшее приближение к истинному значению измеряемой величины принимается среднее арифметическое из всех имеющихся чисел:

Интервал значений физической величины, в который попадает ее истинное значение с некоторой вероятностью α, называется доверительным интервалом. Вероятность α, с которой истинное значение измеряемой величины попадает в доверительный интервал, называется доверительной вероятностью или надежностью.

Если ∆Х - полуширина доверительного интервала, то величина ( - ∆Х) будет нижней границей доверительного интервала, а ( + ∆Х) - верхней границей доверительного интервала.

Используя понятие доверительного интервала и доверительной вероятности, результат измерений некоторой физической величины можно записать в краткой символической форме следующим образом:

( ± ∆Х) с надежностью α.

Как показывается в математической статистике, при малом числе измерений (n <30) полуширина доверительного интервала определяетсяпоформуле:

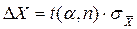
где t(α,n) - коэффициент Стьюдента, зависящий от надежности α и числа измерений n, а - средняя квадратичная погрешность результата серии п измерений, называемая также погрешностью среднего арифметического и определяемая по выражению

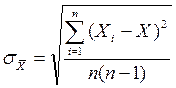
Разности между отдельными значениями X_i и средним

∆X_i=X_i -

называются абсолютными погрешностями отдельных измерений.

Коэффициент Стьюдента определяется по специальным таблицам при заданной надежности (доверительной вероятности) и известном числе измерений. В табл. 14 приведены коэффициенты t при некоторых значениях n и α. При всех измерениях в лабораторном практикуме рекомендуется задавать надежность α = 0,95 (95%).

Таблица 14

Коэффициенты Стьюдента t при различном числе измерений n

в различной надежности α.

n/α	0,90	0,95	0,99	0,999
	6,3	12,7	63,7	636,6
	2,9	4,3	9,9	31,6
	2,4	3,2	5,8	12,9
	2,1	2,8	4,6	8,6
	2,0	2,6	4,0	6,9
	1,9	2,4	3,7	6,0

1. Найти среднее арифметическое из полученных значений измеряемой величины:

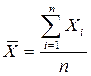
где n - число измерений.

2. Вычислить абсолютные погрешности отдельных измерений:

∆X_i=X_i -

3. Вычислить квадраты абсолютных погрешностей:

(∆Х)² = (Х_i - )²

4. Определить среднюю квадратичную погрешность результата измерений (погрешность среднего арифметического) по формуле:

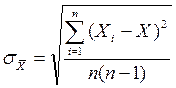
5. Задать значение надежности (доверительной вероятности) α, если нет специальных рекомендаций, принять α=0,95.

6. По таблице найти коэффициент Стьюдента t при заданной надежности α =0,95 и известном числе измерений n.

7. Вычислить полуширину доверительного интервала для случайных погрешностей: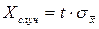

8. Определить суммарную погрешность результата измерений как сумму случайных и систематической погрешностей:

, где

∆ - либо погрешность прибора по его паспорту (если она известна), либо половина наименьшего деления шкалы прибора - δ. В последнем случае ∆=δ/2.

9. Результаты измерений записать в виде

X = ± ∆X_i