 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Поверхностные интегралы
|
|
§ 1. Поверхностные интегралы по простым гладким поверхностям.
1.1. Простая гладкая поверхность.
 Пусть В
Пусть В 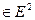 -область, границей которой является простой контур
-область, границей которой является простой контур 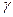 , и пусть функция
, и пусть функция 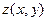 непрерывна в замкнутой области
непрерывна в замкнутой области 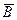
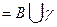 . Обозначим через
. Обозначим через  график этой функции, т.е. поверхность, уравнение которой
график этой функции, т.е. поверхность, уравнение которой 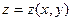 (рис.1):
(рис.1):
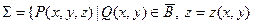
 назовём поверхностью, простой относительно оси
назовём поверхностью, простой относительно оси 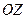 . Пусть точка
. Пусть точка 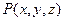 принадлежит поверхно- сти
принадлежит поверхно- сти  . Тогда её проекция на плоскость ХОУ, точка
. Тогда её проекция на плоскость ХОУ, точка 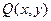 ,, принадлежит замкнутой об- ласти
,, принадлежит замкнутой об- ласти 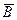 .
. 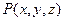 назовём внутренней точкой поверхности
назовём внутренней точкой поверхности  , если
, если 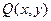 принадлежит В, т.е., является внутренней точкой множества
принадлежит В, т.е., является внутренней точкой множества 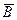 .
. 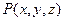 назовём краевой точкой пове- рхности
назовём краевой точкой пове- рхности  , если
, если 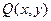 принадлежит
принадлежит 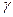 , т.е. является граничной точкой множества
, т.е. является граничной точкой множества 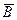 .
.
Множество всех внутренних точек поверхности  назовём внутренностью этой поверх- ности и обозначим через
назовём внутренностью этой поверх- ности и обозначим через 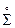 . Множество всех краевых точек поверхности
. Множество всех краевых точек поверхности  назовём кра- ем этой поверхности и обозначим через
назовём кра- ем этой поверхности и обозначим через 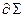 .или через Г. Г является простым контуром, его проекция на плоскость ХОУ есть
.или через Г. Г является простым контуром, его проекция на плоскость ХОУ есть 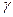 . Если
. Если
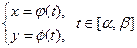 - параметрическое уравнение
- параметрическое уравнение 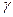 , то
, то
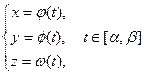 , где
, где 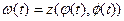 - уравнение Г. При возрастании
- уравнение Г. При возрастании 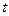 на
на 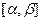 точка
точка 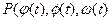 ) совершает обход контура Г. Для наблюдателя, смотрящего с конца оси
) совершает обход контура Г. Для наблюдателя, смотрящего с конца оси 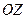 , этот обход совершается либо по часовой стрелке, либо против часовой стрелки. Ниже одну из этих двух ориентаций контура будем называть положительной и применять обозначение
, этот обход совершается либо по часовой стрелке, либо против часовой стрелки. Ниже одну из этих двух ориентаций контура будем называть положительной и применять обозначение 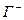 , а другую – отрицательной и применять обозначение
, а другую – отрицательной и применять обозначение 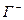 .
.
Пусть точка 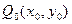 принадлежит области В, а функция
принадлежит области В, а функция 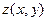 дифференцируе- ма в этой точке. Плоскость, уравнение которой
дифференцируе- ма в этой точке. Плоскость, уравнение которой
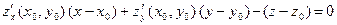 , где
, где 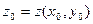 , является касательной плоскостью к поверхности
, является касательной плоскостью к поверхности  в точке
в точке 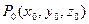 . Прямую, проходящую через
. Прямую, проходящую через 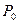 перпендикулярно касательной плоскости называют нор- малью к поверхности
перпендикулярно касательной плоскости называют нор- малью к поверхности  в точке
в точке 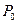 . Вектор
. Вектор  перпендикуля- рен касательной плоскости, он является направляющим вектором нормали в точке
перпендикуля- рен касательной плоскости, он является направляющим вектором нормали в точке 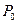 .
.
Ниже считаем, что 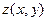 и её частные производные
и её частные производные 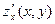 и
и 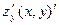 непрерыв- ны в замкнутой области
непрерыв- ны в замкнутой области 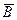 . В этом случае поверхность
. В этом случае поверхность  называют гладкой. Этот термин отражает следующее свойство такой поверхности: при малых перемещениях точки Р по поверхности положение нормали в этой точке меняется плавно, без скачков. Действитель -но, из непрерывности производных
называют гладкой. Этот термин отражает следующее свойство такой поверхности: при малых перемещениях точки Р по поверхности положение нормали в этой точке меняется плавно, без скачков. Действитель -но, из непрерывности производных  и
и 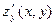 и теоремы о достаточных условиях дифференцируемости вытекает дифференцируемость
и теоремы о достаточных условиях дифференцируемости вытекает дифференцируемость 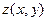 в области В; значит, в каж- дой точке
в области В; значит, в каж- дой точке 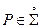 существует касательная плоскость. Введём обозначение:
существует касательная плоскость. Введём обозначение: 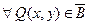
ν (x,y) = 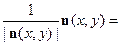
= 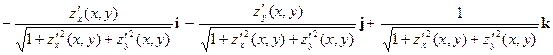 Очевидно, орт ν (x,y) является направляющим вектором нормали к поверхности
Очевидно, орт ν (x,y) является направляющим вектором нормали к поверхности  в точке
в точке  , причём угол между ν (x,y) и ортом k оси
, причём угол между ν (x,y) и ортом k оси  острый. Вектор - функцию ν (x,y) будем называть непрерывной единичной нормалью поверхности
острый. Вектор - функцию ν (x,y) будем называть непрерывной единичной нормалью поверхности  . Непрерывность вектор-функции ν (x,y) обеспечивает плавность изменений положения нормали, о чём было сказано выше. Гладкой поверхностью является, например, полусфера
. Непрерывность вектор-функции ν (x,y) обеспечивает плавность изменений положения нормали, о чём было сказано выше. Гладкой поверхностью является, например, полусфера 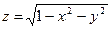 . Обычно орт ν (x,y) будем откладывать от точки
. Обычно орт ν (x,y) будем откладывать от точки 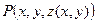 и обозначать его в таком случае через ν (Р).
и обозначать его в таком случае через ν (Р).
Вектор-функцию - ν (x,y) = - ν (Р) также назовём непрерывной единичной норма- лью поверхности  . Угол между ортами - ν (Р) и
. Угол между ортами - ν (Р) и 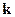 тупой.
тупой.
С векторами ν (Р) и - ν (Р) связаны понятия верхняя и нижняя стороны поверхно- сти  . Понятие “верхняя сторона поверхности
. Понятие “верхняя сторона поверхности  ” складывается из этой поверхности и непрерывной единичной нормали ν (x,y): от каждой точки
” складывается из этой поверхности и непрерывной единичной нормали ν (x,y): от каждой точки 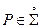 отложен орт ν (Р), обра- зующий с ортом
отложен орт ν (Р), обра- зующий с ортом 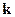 острый угол. Наблюдатель, смотрящий на поверхность
острый угол. Наблюдатель, смотрящий на поверхность  с конца оси
с конца оси 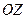 , видит верхнюю её сторону, т.е., поверхность, “ощетинившуюся ” ортами нормали ν (Р),. Аналогично, понятие “ нижняя сторона поверхности
, видит верхнюю её сторону, т.е., поверхность, “ощетинившуюся ” ортами нормали ν (Р),. Аналогично, понятие “ нижняя сторона поверхности  ” состоит из этой поверхно- сти и вектор-функции - ν (x,y). В дальнейшем одну из сторон поверхности – верхнюю или нижнюю – будем обозначать через
” состоит из этой поверхно- сти и вектор-функции - ν (x,y). В дальнейшем одну из сторон поверхности – верхнюю или нижнюю – будем обозначать через 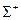 , тогда противоположную сторону обозначаем че- рез
, тогда противоположную сторону обозначаем че- рез 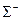 .
.
Ведем понятие о согласовании стороны поверхности и ориентации её края. Пусть 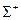 - одна из сторон поверхности
- одна из сторон поверхности  , а
, а 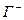 - одна из ориентаций её края. Будем говорить, что сторона
- одна из ориентаций её края. Будем говорить, что сторона 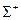 и ориентация края
и ориентация края 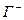 согласованы, если наблюдатель, идущий по сторо- не
согласованы, если наблюдатель, идущий по сторо- не 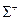 вдоль края
вдоль края 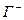 , оставляет поверхность слева от себя. Например, пусть для наблю- дателя, смотрящего с конца оси
, оставляет поверхность слева от себя. Например, пусть для наблю- дателя, смотрящего с конца оси 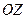 , контур
, контур 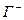 ориентирован против часовой стрелки. Эта ориентация края согласована с верхней стороной поверхности
ориентирован против часовой стрелки. Эта ориентация края согласована с верхней стороной поверхности  .
.
Через 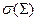 обозначим площадь поверхности
обозначим площадь поверхности  . Справедлива теорема, доказатель- ство которой имеется в [1].
. Справедлива теорема, доказатель- ство которой имеется в [1].
Теорема. Пусть функция 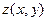 и её частные производные
и её частные производные 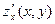 и
и 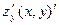 непрерывны в замкнутой области
непрерывны в замкнутой области 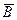 , а
, а  - график этой функции. Тогда
- график этой функции. Тогда
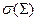
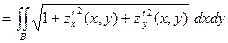 .
.
Край поверхности, её внутренность, верхняя и нижняя стороны поверхности, согла- сование стороны поверхности и ориентации её края - эти понятия введены выше для по- верхности, простой относительно оси 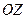 . Те же понятия аналогично вводятся и для по- верхностей, простых относительно других координатных осей, т.е., для поверхностей, за- данных уравнениями видов
. Те же понятия аналогично вводятся и для по- верхностей, простых относительно других координатных осей, т.е., для поверхностей, за- данных уравнениями видов 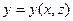 и
и 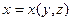 .
.
1.2. Поверхностный интеграл I рода (по площади).
Пусть  - гладкая поверхность, уравнение которой
- гладкая поверхность, уравнение которой 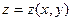 ,
, 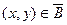 , а
, а 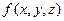 - функция, непрерывная вдоль
- функция, непрерывная вдоль  (т.е.,
(т.е., 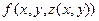 непрерывна на
непрерывна на 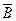 ).
).
Определение. Поверхностным интегралом I рода от функции 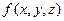 по поверх- ности
по поверх- ности  называют двойной интеграл
называют двойной интеграл 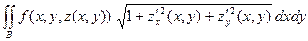
Обозначают введенный интеграл символом 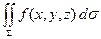 . Таким образом,
. Таким образом,
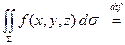
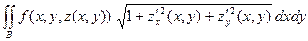 (1)
(1)
Перечислим основные свойства этого интеграла. Ниже 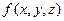 и
и 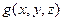 - функции, непрерывные вдоль
- функции, непрерывные вдоль  ,
, 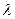 - вещественное число.
- вещественное число.
1. 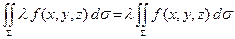 .
.
2. 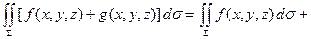
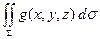 . Эти равенства непосредственно вытекают из сформулированного выше определения и свойств двойного интеграла.
. Эти равенства непосредственно вытекают из сформулированного выше определения и свойств двойного интеграла.
3. 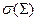 =
= 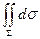 .. Здесь
.. Здесь 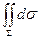 есть интеграл
есть интеграл 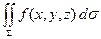 , подынтегральная функция которого тождест- венно на
, подынтегральная функция которого тождест- венно на  равна единице. Положив в (1)
равна единице. Положив в (1) 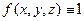 , получим (см. выше, Теорема):
, получим (см. выше, Теорема):
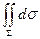
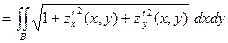 =
= 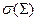 .
.
Определения и свойства поверхностных интегралов 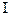 рода по поверхностям, задан- ным уравнениями
рода по поверхностям, задан- ным уравнениями 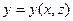 или
или 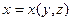 аналогичны изложенным выше. Например, если
аналогичны изложенным выше. Например, если  - график функции
- график функции 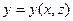 , а
, а 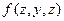 непрерывна вдоль
непрерывна вдоль  , то
, то
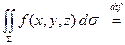
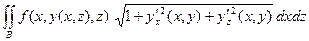 , где В – проекция
, где В – проекция  на плоскость
на плоскость 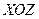 .
.
1.3. Поверхностный интеграл 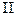 рода (по координатам)
рода (по координатам)
Пусть  - гладкая поверхность, уравнение которой
- гладкая поверхность, уравнение которой 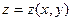 ,
, 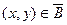 , а ν (Р) – - орт нормали к
, а ν (Р) – - орт нормали к  в точке
в точке 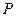 , образующий с ортом
, образующий с ортом 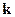 острый угол. Пусть
острый угол. Пусть 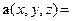
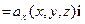
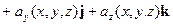 - вектор-функция, непрерывная вдоль этой поверх- ности (т.е., её координатные функции непрерывны вдоль
- вектор-функция, непрерывная вдоль этой поверх- ности (т.е., её координатные функции непрерывны вдоль  ). Зададим на
). Зададим на  функцию
функцию 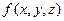 : для любой точки
: для любой точки 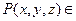
 положим
положим 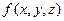 равной проекции вектора
равной проекции вектора 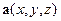 на орт ν (Р)
на орт ν (Р)
Определение 1. Поверхностным интегралом второго рода от вектор - функции 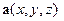 по верхней стороне поверхности
по верхней стороне поверхности  называют поверхностный интеграл первого рода по
называют поверхностный интеграл первого рода по  от проекции вектора
от проекции вектора 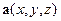 на орт нормали ν (Р).
на орт нормали ν (Р).
Определение 2. Поверхностным интегралом второго рода от вектор - функции 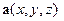 по нижней стороне поверхности
по нижней стороне поверхности  называют поверхностный интеграл первого рода по
называют поверхностный интеграл первого рода по  от проекции вектора
от проекции вектора 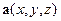 на орт нормали - ν (Р).
на орт нормали - ν (Р).
Для поверхностей, простых относительно осей 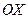 и
и 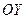 , нетрудно сформулиро- вать аналогичные определения.
, нетрудно сформулиро- вать аналогичные определения.
Пусть  - гладкая поверхность, простая относительно одной из координатных осей. Одну из сторон этой поверхности – верхнюю или нижнюю – обозначим через
- гладкая поверхность, простая относительно одной из координатных осей. Одну из сторон этой поверхности – верхнюю или нижнюю – обозначим через 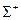 , а противоположную сторону через
, а противоположную сторону через 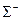 . Орт нормали на стороне
. Орт нормали на стороне 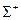 обозначим через ν
обозначим через ν 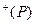 , а на стороне
, а на стороне 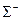 - через ν
- через ν 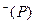 . Направление орта ν
. Направление орта ν 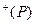 назовём положительным направле- нием нормали, направление орта ν
назовём положительным направле- нием нормали, направление орта ν 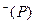 – отрицательным направлением нормали. Заме- тим:
– отрицательным направлением нормали. Заме- тим: 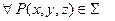 ν
ν 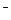 (Р) = - ν
(Р) = - ν 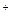 (Р). Пусть
(Р). Пусть 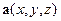 - вектор – функция, непрерывная вдоль
- вектор – функция, непрерывная вдоль  . Сформулируем определение, обобщающее те, что приведёны выше.
. Сформулируем определение, обобщающее те, что приведёны выше.
Пусть  - гладкая поверхность, простая относительно одной из координатных осей, а вектор-функция
- гладкая поверхность, простая относительно одной из координатных осей, а вектор-функция 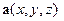 непрерывна вдоль
непрерывна вдоль  .
.
Определение 3. Поверхностным интегралом второго рода от вектор - функции 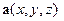 по стороне
по стороне 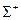 (по стороне
(по стороне 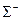 ) поверхности
) поверхности  называют поверхностный интег- рал первого рода по
называют поверхностный интег- рал первого рода по  от проекции вектора
от проекции вектора 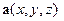 на положительное (отрицательное) направление нормали в точке
на положительное (отрицательное) направление нормали в точке 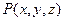
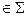 .
.
Поверхностный интеграл по стороне 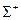 обозначать будем символами
обозначать будем символами
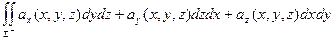 и
и 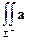 d Σ.. Заменив в этих символах
d Σ.. Заменив в этих символах  на
на  , получим обозначения для интеграла по стороне
, получим обозначения для интеграла по стороне 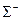 .
.
Проекция вектора 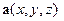 на тот или иной орт равна скалярному произведению этих векторов; поэтому
на тот или иной орт равна скалярному произведению этих векторов; поэтому
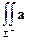 d Σ
d Σ 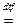
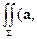 ν
ν 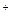 )
) 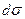 ,
, 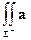 d Σ
d Σ 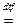
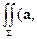 ν
ν 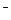 )
) 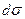
Перечислим основные свойства введённого интеграла. Ниже 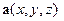 и
и 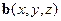 - вектор – функции, непрерывные вдоль
- вектор – функции, непрерывные вдоль  ,
, 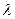 - вещественное число.
- вещественное число.
1. 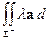 Σ =
Σ = 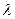
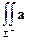 d Σ.
d Σ.
2. 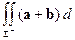 Σ =
Σ = 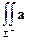 d Σ +
d Σ + 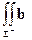 d Σ.
d Σ.
Эти равенства непосредственно вытекают из сформулированного выше определе- ния и свойств поверхностного интеграла 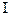 рода.
рода.
3. 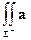 d Σ = -
d Σ = - 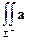 d Σ.
d Σ.
► Так как 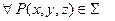 ν
ν  (Р) = - ν
(Р) = - ν  (Р), то
(Р), то
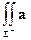 d Σ
d Σ 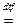
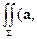 ν
ν 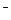 )
) 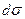 =
= 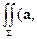 - ν
- ν 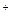 )
) 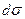 = -
= - 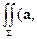 ν
ν 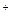 )
) 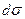
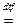 -
- 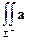 d Σ. ◄
d Σ. ◄
Пусть 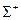 есть верхняя сторона гладкой поверхности
есть верхняя сторона гладкой поверхности  , простой относительно одной из координатных осей.. Выпишем формулы, выражающие поверхностный интеграл по
, простой относительно одной из координатных осей.. Выпишем формулы, выражающие поверхностный интеграл по 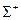 через двойной интеграл по проекции этой поверхности на соответствующую коор- динатную плоскость..
через двойной интеграл по проекции этой поверхности на соответствующую коор- динатную плоскость..
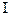 . Если
. Если  задана уравнением
задана уравнением 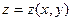 , а
, а 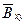 - проекция
- проекция  на плоскость
на плоскость 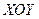 , то
, то
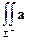 d Σ =
d Σ = 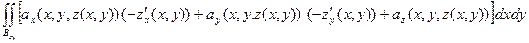 .
.
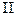 . Если
. Если  задана уравнением
задана уравнением 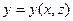 , а
, а 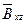 - проекция
- проекция  на плоскость
на плоскость 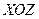 , то
, то
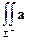 d Σ =
d Σ = 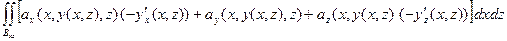 .
.
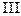 . Если
. Если  задана уравнением
задана уравнением 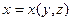 , а
, а 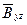 - проекция
- проекция  на плоскость
на плоскость 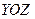 , то
, то
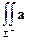 d Σ =
d Σ = 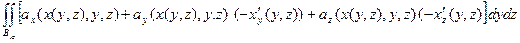
► Докажем формулу 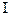 ; доказательства других двух аналогичны. По определению
; доказательства других двух аналогичны. По определению 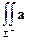 d Σ =
d Σ = 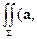 ν
ν 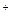 )
) 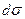 , где
, где
ν 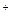 = ν (х,у) =
= ν (х,у) = 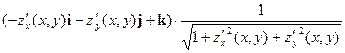 .
.
Значит,
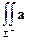 d Σ
d Σ 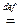
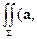 ν
ν 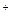 )
) 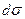
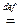
= 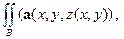 ν (х,у))
ν (х,у)) 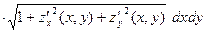 =
=
= 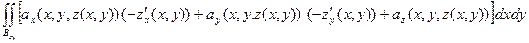 . ◄
. ◄
. 1.4. Формула Стокса.
Пусть функции 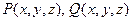 и
и 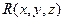 непрерывны и имеют непрерывные частные производные первого порядка по каждому из своих аргументов в некоторой об- ласти
непрерывны и имеют непрерывные частные производные первого порядка по каждому из своих аргументов в некоторой об- ласти 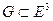 . Обозначим:
. Обозначим:
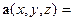
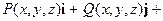
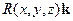 ;
;
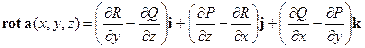 . Таким образом, в области
. Таким образом, в области 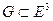 определены два векторных поля:
определены два векторных поля: 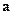 и
и 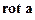 ; поле
; поле 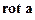 называют ротором (вихрем) поля а. Равенство
называют ротором (вихрем) поля а. Равенство 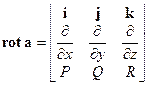 - это удобный для запоминания способ записать этот вектор.
- это удобный для запоминания способ записать этот вектор.
Пусть  - гладкая и простая относительно одной из координатных осей поверх- ность, а
- гладкая и простая относительно одной из координатных осей поверх- ность, а 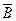 - проекция
- проекция  на координатную плоскость, перпендикулярную этой координат- ной оси. Будем считать
на координатную плоскость, перпендикулярную этой координат- ной оси. Будем считать 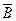 областью, ограниченной простым кусочно-гладким контуром.Булем также считать, что
областью, ограниченной простым кусочно-гладким контуром.Булем также считать, что  содержится в области
содержится в области 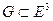 , в которой определены поля
, в которой определены поля 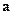 и
и 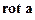 .
.
Теорема. Пусть поверхность  и вектор-функция
и вектор-функция 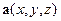 удовлетворяют указан- ным выше условиям. Тогда
удовлетворяют указан- ным выше условиям. Тогда 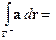
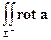 d Σ, где
d Σ, где 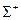 - одна из сторон поверхности
- одна из сторон поверхности  , а Г
, а Г 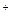 - край
- край  , ориентация которого согласована со стороной
, ориентация которого согласована со стороной 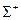 .
.
► Доказательство приведём для случая, когда  - простая относительно оси
- простая относительно оси 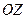 поверхность, а
поверхность, а 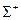 - верхняя её сторона.
- верхняя её сторона.
Пусть В – область в плоскости 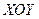 , границей В является простой кусочно-гладкий кон- тур
, границей В является простой кусочно-гладкий кон- тур 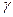 , заданный параметрическим уравнением
, заданный параметрическим уравнением 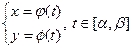 . Функция
. Функция 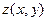 , а также её частные производные
, а также её частные производные 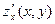 и
и 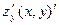 непрерывны в замкнутой области
непрерывны в замкнутой области 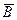 .
.
Введем в рассмотрение три вектор-функции:
. 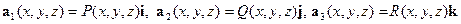 . Очевидно,
. Очевидно, 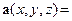
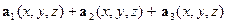 . Кроме того, нетрудно убедиться в справедливости равенства
. Кроме того, нетрудно убедиться в справедливости равенства 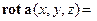
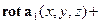
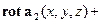
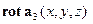 . Докажем три равенства:
. Докажем три равенства:
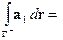
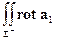 d Σ,
d Σ, 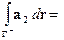
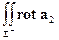 d Σ,
d Σ, 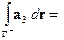
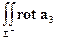 d Σ. (2)
d Σ. (2)
Так как 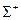 - верхняя сторона поверхности
- верхняя сторона поверхности  , то согласованная с ней ориентация Г
, то согласованная с ней ориентация Г 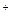 её края - против часовой стрелки. Будем считать, что уравнение
её края - против часовой стрелки. Будем считать, что уравнение 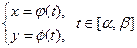 ориентирует контур
ориентирует контур 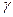 против часовой стрелки. Тогда уравнение
против часовой стрелки. Тогда уравнение
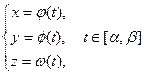 , где
, где 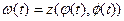 есть уравнение Г
есть уравнение Г 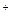 . Докажем первое из равенств (2). По формуле I, п.!.3., имеем:
. Докажем первое из равенств (2). По формуле I, п.!.3., имеем: 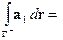
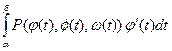 . Обозначим:
. Обозначим: 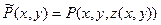 . Тогда (см. глава “Криволинейные интегралы”, п. 3.2., свойство 4, формула 7)):
. Тогда (см. глава “Криволинейные интегралы”, п. 3.2., свойство 4, формула 7)): 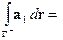
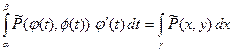 . Положим
. Положим 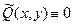 на множестве
на множестве  . По формуле Грина
. По формуле Грина 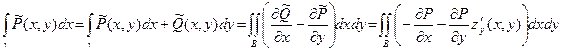 . Таким образом,
. Таким образом, 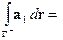 -
- 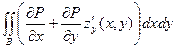 (3)
(3)
С другой стороны (см. (3), а также формулу I, п. 1.3),
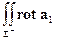 d Σ =
d Σ = 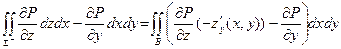 =
=
= - 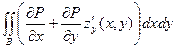 . (4)
. (4)
Из (3) и (4) следует: 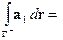
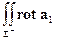 d Σ.
d Σ.
Доказательство второго из равенств (2) проводится аналогично.
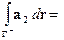
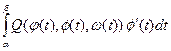 . Обозначим:
. Обозначим: 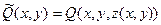 . Тогда (см. глава “Криволинейные интегралы”, п. 3.2., свойство 4, формула 7)):
. Тогда (см. глава “Криволинейные интегралы”, п. 3.2., свойство 4, формула 7)): 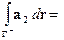
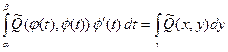 . Положим
. Положим 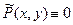 на множестве
на множестве 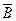 . По формуле Грина
. По формуле Грина 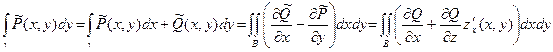 . Таким образом,
. Таким образом, 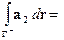
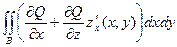 (5)
(5)
С другой стороны (см. (3), а также формулу I, п. 1.3),
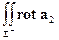 d Σ =
d Σ = 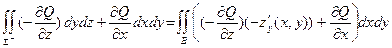 =
=
= 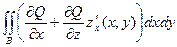 . (6)
. (6)
Из (5) и (6) следует: 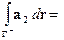
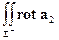 d Σ.
d Σ.
Докажем третье из равенств (2). С целью упростить доказательство наложим на функцию 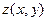 дополнительное требование: в
дополнительное требование: в 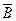 существуют и непрерывны смешанные производные
существуют и непрерывны смешанные производные 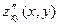 и
и 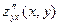 . По теореме о равенстве смешанных производных
. По теореме о равенстве смешанных производных 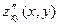 =
= 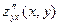 в В. Напомним:
в В. Напомним: 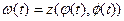 .
.
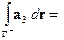 =
= 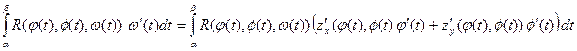 .
.
Пусть 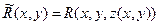 . Тогда
. Тогда
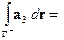
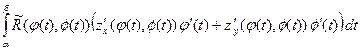 =
=
= 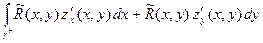
По формуле Грина
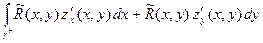 =
=
= 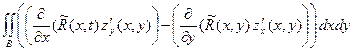 = =
= = 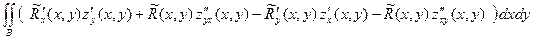 = =
= = 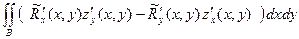 =
= 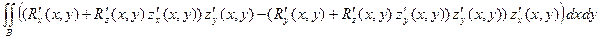 = =
= = 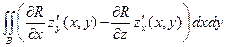
Таким образом, 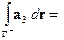
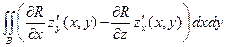 . С другой стороны,
. С другой стороны,
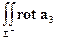 d Σ =
d Σ = 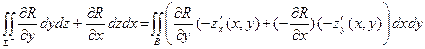
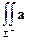 d Σ =
d Σ = 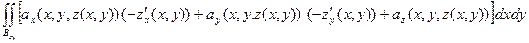 .= =
.= = 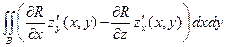 .
.
Значит, справедливо и третье из равенств (2). Сложив эти три равенства почленно, полу- чим формулу Стокса для случая, когда  - простая относительно оси
- простая относительно оси 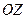 поверхность, а
поверхность, а 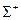 - верхняя её сторона. Для других могущих иметь место случаев доказательства можно построить аналогично изложенному выше. ◄
- верхняя её сторона. Для других могущих иметь место случаев доказательства можно построить аналогично изложенному выше. ◄
1.5. Поверхностный интеграл как предел последовательности интегральных сумм.
Пусть 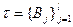 - некоторое дробление области
- некоторое дробление области 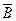 , т.е., множества
, т.е., множества 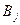 ,
, 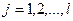 измеримы, попарно не пересекаются и
измеримы, попарно не пересекаются и 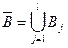 . Обозначим через
. Обозначим через 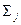 график функции
график функции 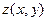 на множестве
на множестве 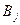 ; т.е.,
; т.е., 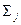 - та часть поверхности
- та часть поверхности  , проекцией которой на плос- кость
, проекцией которой на плос- кость 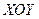 является
является 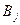 . Совокупность
. Совокупность 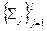 обозначим через
обозначим через 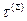 и назовём дроблени- ем поверхности
и назовём дроблени- ем поверхности  :
: 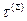 =
= 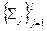 . Заметим:
. Заметим: 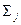 ,
, 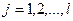 попарно не пересекаются, и
попарно не пересекаются, и 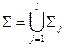 . В тех случаях, когда требуется различать стороны
. В тех случаях, когда требуется различать стороны 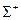 и
и 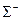 , применяем обозна- чения
, применяем обозна- чения 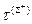 =
= 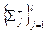 и
и 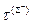 =
= 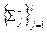 .
.
Пусть 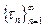 - нормальная последовательность дроблений области
- нормальная последовательность дроблений области 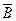 . Соответст- вующую последовательность
. Соответст- вующую последовательность 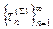 назовём нормальной последовательностью дробле- ний поверхности
назовём нормальной последовательностью дробле- ний поверхности  .
.
Пусть 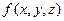 и
и 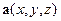 - скалярная и векторная функции, определённые в точках поверхности
- скалярная и векторная функции, определённые в точках поверхности  и непрерывные вдоль неё. Пусть
и непрерывные вдоль неё. Пусть 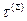 =
= 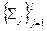 - некоторое дробление поверхности
- некоторое дробление поверхности  , а точка
, а точка 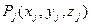 произвольно взята на
произвольно взята на 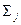 . Обозначим:
. Обозначим:
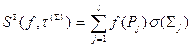 ,
, 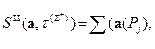 ν
ν 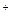 (
(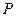
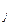 ))
)) 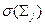 . Эти суммы назовем интегральными суммами по дроблению
. Эти суммы назовем интегральными суммами по дроблению 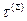 скалярной функции
скалярной функции 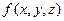 и векторной функции а
и векторной функции а 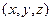 . Справедливы утверждения (см. [1]): для любой нормальной последовательности
. Справедливы утверждения (см. [1]): для любой нормальной последовательности 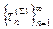 дроблений поверхности
дроблений поверхности 
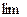
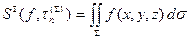 ,
, 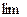
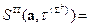
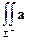 d Σ.
d Σ.
§ 2. Поверхностные интегралы по кусочно - гладким поверхностям.
2. 1. Кусочно – гладкая ориентируемая поверхность.
Пусть 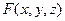 - функция, непрерывная в некоторой области трехмерного прост- ранства, а
- функция, непрерывная в некоторой области трехмерного прост- ранства, а  - геометрическое место точек
- геометрическое место точек 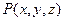 , координаты которых удовлетворяют уравнению
, координаты которых удовлетворяют уравнению 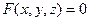 . Геометрическое место
. Геометрическое место  назовем поверхностью, а уравнение
назовем поверхностью, а уравнение 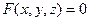 - уравнением этой поверхности.
- уравнением этой поверхности.
Пример. Пусть 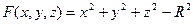 , где
, где 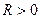 . Уравнение
. Уравнение 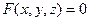 есть уравнение сферы.
есть уравнение сферы.
Геометрическое место  может оказаться объектом весьма сложной структуры. Но поверхности, представляющие интерес для приложений, обычно не столь сложны. Как правило, в прикладных задачах рассматривают поверхности либо простые относительно той или иной координатной оси, либо такие, что их можно разбить на несколько частей, каждая из которых является поверхностью, простой относительно одной из координат- ных осей. В этом пункте рассматриваем поверхности именно такого типа.
может оказаться объектом весьма сложной структуры. Но поверхности, представляющие интерес для приложений, обычно не столь сложны. Как правило, в прикладных задачах рассматривают поверхности либо простые относительно той или иной координатной оси, либо такие, что их можно разбить на несколько частей, каждая из которых является поверхностью, простой относительно одной из координат- ных осей. В этом пункте рассматриваем поверхности именно такого типа.
Пусть поверхность  разделена сетью кривых на
разделена сетью кривых на 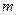 частей
частей 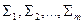 . Будем записывать
. Будем записывать 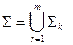 и будем считать выполненными следующие условия.
и будем считать выполненными следующие условия.
1. Каждая из частей 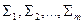 представляет собой простую относительно одной из координатных осей и гладкую поверхность, т.е., является графиком функции
представляет собой простую относительно одной из координатных осей и гладкую поверхность, т.е., является графиком функции 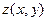
 функции
функции 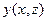 , функции
, функции 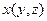
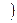 , непрерывной вместе со своими частными произ- водными первого порядка в некоторой ограниченной замкнутой области.
, непрерывной вместе со своими частными произ- водными первого порядка в некоторой ограниченной замкнутой области.
2. Край 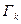 поверхности
поверхности 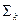 ,
, 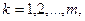 есть кусочно-гладкий простой контур.
есть кусочно-гладкий простой контур.
3. При 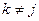 поверхности
поверхности 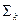 и
и 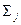 не имеют общих внутренних точек.
не имеют общих внутренних точек.
4.  - связное множество.
- связное множество.
Если эти условия соблюдены, будем называть поверхность 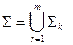 кусочно- гладкой поверхностью.
кусочно- гладкой поверхностью.
Пусть 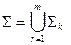 - кусочно-гладкая поверхность,
- кусочно-гладкая поверхность, 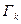 - край поверхности
- край поверхности 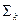 ,
, 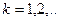
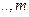 . Пусть точка Р – краевая для какой-либо из поверхностей
. Пусть точка Р – краевая для какой-либо из поверхностей 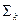 , т.е.,
, т.е., 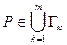 . Возмож- ны два случая: 1) Р лежит только на одном из контуров
. Возмож- ны два случая: 1) Р лежит только на одном из контуров 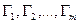 и 2) Р является общей по крайней мере для двух из этих контуров. Множество всех точек, удовлетворяющих ус- ловию 1) обозначим через
и 2) Р является общей по крайней мере для двух из этих контуров. Множество всех точек, удовлетворяющих ус- ловию 1) обозначим через 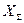 . Точку Р,
. Точку Р, 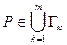 , назовём краевой точкой кусочно -гладкой поверхности
, назовём краевой точкой кусочно -гладкой поверхности  в двух случаях: 1) Р принадлежит только одному из контуров
в двух случаях: 1) Р принадлежит только одному из контуров 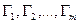 , т.е.,
, т.е., 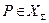 , и 2) Р является предельной точкой множества
, и 2) Р является предельной точкой множества 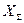 .
.
Множество всех краевых точек поверхности  назовём краем этой поверхности
назовём краем этой поверхности
Замечание. Пусть 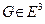 - ограниченная область, а её граница представляет собой кусочно – гладкую поверхность
- ограниченная область, а её граница представляет собой кусочно – гладкую поверхность  . Такая поверхность края не имеет, поскольку для неё множество
. Такая поверхность края не имеет, поскольку для неё множество 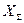 пусто. В этом случае поверхность
пусто. В этом случае поверхность  называют замкнутой. К замкнутым поверхностям принадлежат сфера, эллипсоид, параллелепидед, пирамида и т.п. Замкнутая поверхность разбивает пространство
называют замкнутой. К замкнутым поверхностям принадлежат сфера, эллипсоид, параллелепидед, пирамида и т.п. Замкнутая поверхность разбивает пространство 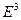 на две части – ограниченную (её называют внут- ренностью поверхности) и неограниченную(её называют внешностью поверхности).
на две части – ограниченную (её называют внут- ренностью поверхности) и неограниченную(её называют внешностью поверхности).
Пусть 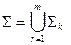 - некоторая кусочно-гладкая поверхность При
- некоторая кусочно-гладкая поверхность При 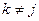 поверхности
поверхности 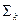 и
и 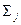 не имеют общих внутренних точек, но общие граничные точки у них могут быть. Две поверхности
не имеют общих внутренних точек, но общие граничные точки у них могут быть. Две поверхности 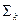 и
и 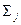 ,
, 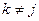 , назовём соседними, если края этих поверхностей, конту- ры
, назовём соседними, если края этих поверхностей, конту- ры 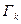 и
и 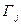 , имеют общую часть, т.е., если существует некоторая дуга
, имеют общую часть, т.е., если существует некоторая дуга 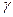 , принадлежащая и
, принадлежащая и 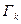 , и
, и 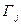 .
.
Дата публикования: 2015-07-22; Прочитано: 354 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
