Гармонический осциллятор

Лекция № 9

Дифференциальное уравнение гармонических колебаний

Уравнение, которому должна подчиняться переменная 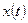, чтобы изменяться по гармоническому закону 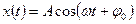имеет вид

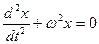. (1)

Для доказательства используем прямую подстановку этого уравнения в уравнение гармонических колебаний. В комплексной форме переменная 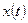может быть представлена в виде

.

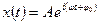Тогда

;

.

Следовательно,

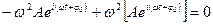
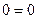
Это значит, что уравнение (1) является дифференциальным уравнением гармонических колебаний.

Свободные колебания осциллятора

Примеры колебательных систем

а) Грузик на пружине

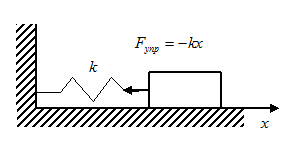Грузик располагается на гладком столе. Запишем ІІ закон Ньютона

.

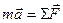Спроектировав на ось х, получим

.

; ; .

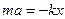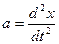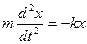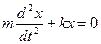Отсюда

.

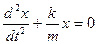Сравним с (1).

Получим дифференциальное уравнение гармонических колебаний с частотой .

.

Соответственно, уравнение для смещения имеет вид

.

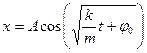Амплитуда и начальная фаза колебаний определяются условиями возбуждения.

б) Физический маятник

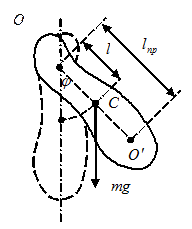Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции.

В положении равновесия центр инерции маятника 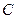находится под точкой подвеса маятника 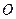на одной вертикали. При отклонении маятника от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия:

,

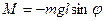где 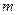- масса маятника;

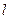- расстояние между точкой подвеса и центром инерции маятника.

Такое действие аналогично квазиупругой силе, поэтому в левой части уравнения берем знак (-).

Запишем основное уравнение динамики вращательного движения

,

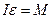где 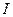- момент инерции маятника относительно оси, проходящей через точку подвеса;

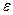- угловое ускорение маятника.

Подставим вместо 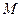его выражение, тогда

.

.

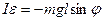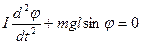Полученное дифференциальное уравнение нелинейно (функция есть нелинейная функция. Поэтому колебания физического маятника будут негармоническими).

Для случая малых колебаний 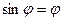и уравнение примет вид

(: )

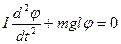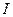или

.

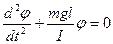Обозначим через 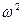, тогда

.

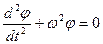Решив это уравнение, получим

.

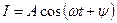Следовательно, при малых колебаниях физического маятника от положения равновесия он совершает гармонические колебания.

Период колебаний определится из выражения

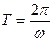. Т.к. 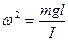, то

.

Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см. точку 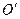на рисунке).

При подвешивании маятника в центре качания приведенная длина, а следовательно и период колебаний, остаются теми же, что и в начале. Следовательно, точка подвеса и центр качания обладают свойствами взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится центром качания.

На свойстве взаимности основано определение ускорения силы тяжести с помощью оборотного маятника.

Оборотным маятником называется такой маятник, у которого вблизи его концов имеются две призмы, за которые он может поочередно подвешиваться.

Вдоль маятника могут перемещаться и закрепляться на нем тяжелые грузы. Передвигая грузы, добиваются чтобы, при подвешивании маятника за любую из призм, его период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно .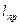

Измерив период колебаний и 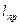, можно найти 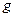из формулы

.

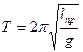Мы рассмотрим случай небольших отклонений физического маятника от положения равновесия. При больших углах отклонения маятник будет совершать более сложное периодическое колебательное движение. Период этого негармонического колебания зависит от амплитуды колебания и возрастает с ее увеличением.

в) Математический маятник

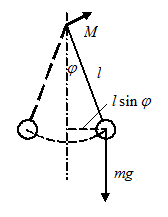Математическим маятником называется идеализированная система, состоящая из невесомой нерастяжимой нити, на которой подвешена масса, сосредоточенная в данной точке.

Обозначим через угол, образованный максимальным отклонением нити с вертикалью.

При отклонении маятника от положения равновесия возникает вращательный момент :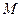

.

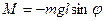Запишем основное уравнение динамики вращательного движения:

,

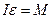где 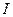- момент инерции маятника. Величина его равна .

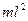Подставив в это уравнение вместо 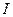и 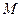их выражения, получим:

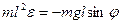
или в ином виде

.

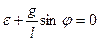Воспользуемся разложением в ряд Тейлора:

.

Это значит, что для малых углов отклонения от вертикали, порядка 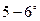, можно считать, что 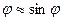, тогда

.

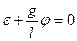Обозначим 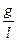через 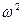и вспомним, что .

.

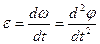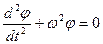Решая это уравнение, получим:

.

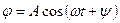Следовательно, при малых колебаниях маятника угловое отклонение изменяется со временем по гармоническому закону.

Так как 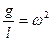, а частота гармонических колебаний связана с периодом соотношением 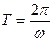, то

.

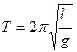Пользуясь этой формулой с помощью математического маятника можно определить ускорение силы тяжести. Поэтому математический маятник используют в геологоразведке, если ускорение силы тяжести больше или меньше нормального, то это указывает, что в данном месте имеется наличие полезных ископаемых, соответственно большей плотности, чем средняя плотность земной коры (металлическая руда) или меньшей (нефть, соль).

Сопоставив формулу периодов колебаний математического и физического маятников, мы видим, что математический маятник с длиной 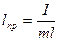имеет такой же период колебаний, как и данный физический маятник.

Величину 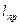называют приведенной длиной физического маятника.

Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

г) Колебательный - контур

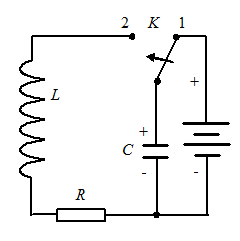Рассмотрим процессы, происходящие в электрической схеме после переключения ключа в положение 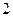. Конденсатор 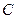, накопивший заряд 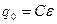, начнет разряжаться через катушку индуктивности и сопротивление .

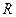В силу явления самоиндукции ток нарастает не сразу, но зато достигнув максимума в момент полного разряда конденсатора (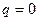) не сразу и исчезает, вызывая перезаряд конденсатора.

Затем начнется обратный процесс и в цепи возникнут колебания заряда (или тока), при котором энергия перераспределяется между конденсатором 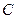и катушкой , частично переходя в тепло на сопротивление .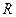

Выведем дифференциальное уравнение возникающих электромагнитных колебаний. Запишем ІІ-е правило Кирхгофа

.

; ; .

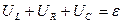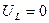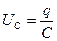Полагаем, что катушка индуктивности идеальна

, .

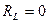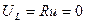Тогда .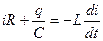

Поскольку 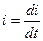, то это уравнение можно записать в виде

.

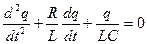Для идеального контура, где , имеем

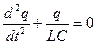. (1)

По своей форме это уравнение совпадает с дифференциальным уравнением гармонических колебаний. Роль играет 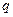. Роль 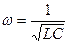. Тогда период колебаний

- формула Томсона.

Решением уравнения (1) будет функция

.

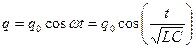Условия возбуждения колебаний будут 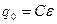и 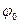. В других схемах значения 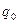и 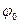могут стать иными, но частота колебаний 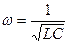не изменится, так как она определяется только свойствами самой колебательной системы.

Общие выводы: