Проверка адекватности полученной модели

Проверка адекватности полученной модели как правило выполняется на основании следующей гипотезы: отклонение экспериментальных значений от расчетных является минимальным и незначимо отличается от ошибки опыта. Это выполняется с использованием F-критерия Фишера. Если расчетное значение F-критерия меньше табличного, есть основание считать полученное уравнение адекватным.

При проверке адекватности прежде всего необходимо оценить сумму квадратов отклонений экспериментальных значений от рассчитанных по полученным формулам во всех точках плана. Для этого после расчетов по полученному уравнению регрессии заполняется 13 столбец матрицы планирования (табл.1).

Эта величина называется остаточной суммой квадратов .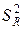

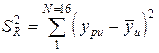
Остаточная дисперсия ли дисперсия адекватности 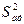получается путем деления остаточной суммы квадратов 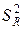на число степеней свободы N-m,

где N-число опытов плана m- число значащих членов в уравнении регрессии, получаем .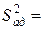

Расчетное значение критерия Фишера F_р определяют по формуле:

Табличное значение критерия Фишера определяется при степенях свободы: f₁=N-m=, а f₂=N*(k-1) для выбранного уровня значимости (обычно 0,05)

При F_р 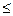F_т есть основание полагать, что уравнение адекватно.

Если модель получается неадекватной, можно попытаться линеаризовать модель с помощью принятия за основу степенной зависимости, которую можно линеаризовать с помощью логарифмирования.

Например:

после линеаризации:

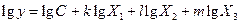
Планы второго порядка

В матрице планирования первого порядка каждая из переменных варьировалась на двух уровнях. Для оптимизациизависимости полиномом второго порядка изучение только на двух уровнях уже недостаточно и, следовательно, в план должны включаться дополнительные точки для увеличения количества уровней каждого фактора.

Можно предположить, что наиболее простыми эффективными окажутся планы, включающие полный факторный эксперимент типа 3^k т. е. с варьированием каждой переменной на трех уровнях. Но при этом с ростом числа факторов значительно увеличивается количество опытов. Так, N=27 при k=3, а при k=5 N=243 и т. д. Реализация такого большого количества опытов часто практически невозможна и не нашла применения при планировании эксперимента.

Гораздо эффективнее оказались специальные планы второго порядка на пяти уровнях. Основу такого планирования, его ядро составляет полный факторный эксперимент линейного приближения типа 2^k, к которому добавляется определенное количество специально распо­ложенных точек. Поэтому такие планы называются композиционными. Присоединенные к ядру так называемые звездные точки характеризуются величиной звездного плеча которое определяет расстояние от них до центра эксперимента. Третью группу образуют опыты в нулевой точке. Таким образом общее число экспериментальных точек в плане второго порядка определяется соотношением N=2^k+2•k+n_о (где k -число факторов; n_о — количество опытов в нулевой точке).

Как видно, каждый из факторов варьируется не менее чем на трех уровнях. Преимущество таких планов по сравнению с полным факторным экспериментом типа 3^k очевидно. Действительно, при k=3 и n_о=1 N=15 вместо 27, при k=4 N=25 вместо 81 и т.д.

Ротатабельные планы

Всякий план будет ротатабельным только тогда, когда экспериментальные точки будут лежать не менее чем на двух сферах (в общем случае, для k-мерного пространства,—на двух гиперсферах).

В качестве первой сферы с нулевым радиусом выбирают центральную точку плана — центр эксперимента. Тогда все остальные опыты будут располагаться на второй сфере выбранного радиуса r и будут равно удалены от нулевой точки.

В частном случае, для плана второго порядка при k=2 (плоская задача) вместо сфер можно рассматривать две окружности. Графическое построение такого плана представлено на рис. 1.

Вершины квадрата здесь соответствуют координатам экспе­риментальных точек полного факторного эксперимента типа 2^k, если вокруг данного квадрата описать окружность с центром в нулевой точке, то ее пересечение с центральными осями даст координаты четырех дополнительных звездных точек (±a, 0 и 0±a). Таким образом, все экспериментальные точки лежат на двух окружностях. Первая - в центре эксперимента с нулевым радиусом, а вторая с радиусом r=a (величина звездного плеча). Из геометрических соотношений легко определить значение a для данного случая. Как видно, a²=1²+1² и a= . В общем случае при числе переменных равном k величина звездного плеча определяется соотношениями a 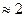^k/4.

Количество опытов в нулевой точке назначается из условия получения равной информации о процессе как в центре экспе­римента, так к в периферийных точках и зависит от числа вклю­ченных в рассмотрение факторов Такой план называется униформ - планом. Значения величии n_о для ротатабельного планирования табулированы и приведены в литературе (Ю.П. Адлер Введение в планирование эксперимента, М., «Металлургия», 1969; В.В. Налимов и Н.А. Чернова Статистические методы планирования экстремальных экспериментов). Рассмотренный метод построения определяет центральное композиционное ротатабельное униформ планирование второго порядка.

Матрица такого планирования представлена в табл.. В нее включен без изменения ПФЭ типа 2³, т. е. основные (с 1 по 8) и дополнительные (с 9 по 14) опыты с звезд­ным плечом a 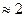^{k/4 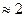3/4}=1,682 и опыты (с 15 по 20) в нулевой точке. Для реализации такого плана, используя весь предыду­щий материал, достаточно провести лишь шесть опытов в звезд­ных точках.

Обработка полученных данных для расчета коэффициентов полного квадратного уравнения ведется по сравнительно сложным формулам. Для нашего случая при к=3 эти формулы имеют вид:

b₀=0,166338(0y) - 0,056791 ;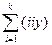

b₁ = 0,073224 (iy)

b ii = 0,0625(iiy)+0,006889 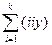- 0,056791 (Oy),

b ij = 0,125(ijy),

(Oy) ,= ,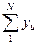

(iiy)= ,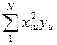

(iy)= ,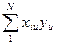

(ijy),= ,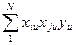

i, j - номера столбцов матрицы планирования;

u - номер строки,

N - количество опытов в плане.

Статистическй анализ результатов для планов второго прядка

При проведении статистического анализа полученного уравнения регрессии воспользуемся рассмотренной ранее методической схемой для ПФЭ.

Оценка дисперсии, характеризующей ошибку опыта. Определение ошибки опыта проводилось на каждом этапе исследований: для первой и второй полуреплик, для полного факторного эксперимента, для опытов в нулевой точке. Раннее было подтверждено, что все вычисленные дисперсии однородны, т. е. практически равны. Следовательно, для дальнейшего статистического анализа можно использовать любую из рассчитанных дисперсий: построчную S _i², усредненнyю S _ср² дисперсию в нулевой точке S ₀² и т. д.

Выбор той или иной оценки в некоторой степени произволен. Однако очевидно, что при ротатабельном планировании эксперимента удобнее оценивать дисперсию по результатам опытов в нулевой точке, так как дублирование этих опытов предусмотрено самим планом эксперимента (опыты с 15 по 20 в матрице планирования). В качестве оценки ошибки опыта примем дисперсию в нулевой точке S_y ² f_y=n_o— 1

Определение значимости коэффициентов регрессии. Расчет дисперсий при определении коэффициентов производится до следующим формулам:

S²(b₀)=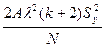

S²(b_i)=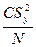

S²(b_ii)=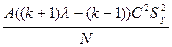

S²(b_ij)=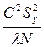

где С = ; А= ;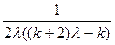

.

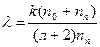Значимость коэффициентов определяется с помощью t- критерия Стьюдента. Если коэффициент статистически значим, то влияние соответствующего фактора существенно. Однако обратное утверждение не всегда справедливо. Поэтому при окончательной записи уравнения нельзя исключать значимые коэффициенты и в то же врем по чисто технологическим соображениям допускается введения любого статистически незначимого коэффициента.

При проверке адекватности полученной модели, как и для линейный планов, прежде всего вычисляется остаточная сума квадратов S_R

S_R=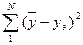

Далее рассчитывается сумма квадратов, связанную с повторением опытов в нулевой точке S_E.

S_{Е =}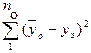

Для расчета дисперсии адекватности необходимо определить число степеней свободы системы.

f_ад=N - m - (n_o - 1),

где N- общее число опытов в плане,

m - число коэффициентов, включенных в модель,

n_о - число опытов в нулевой точке.

Адекватность проверяем по F - критерию Фишера

при f₁ = f_ад, f₂ = f₀