 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Условия подобия
|
|
Механическое моделирование использует геометрическое и физическое подобие. Пусть координаты натурного объекта описываются функцией — f(X H, FH, Z H ), а координаты соответственных точек модели — fm(x M, у M, zM). Тогда при полном геометрическом подобии масштаб
m = xM/XH = yM/YH = zM/ZH.
При механическом моделировании помимо геометрического подобия необходимо также воспроизвести физическое подобие явлений, протекающих и в модели, и в натуре, например, напряженного состояния, форм колебаний и т. п. Если в натурном объекте изучаемая величина, например, перемещение является функцией ряда определяющих ее параметров
UH = = F(UH,1, UH,2, …, UH,n),
где UH,1, UH,2, …, UH,n — механические характеристики материала, физические величины, характеризующие нагрузки и т. д., а соответственные величины, определяющие перемещение точек модели, связаны зависимостью
uм = Ф(uм,1, uм,2, …, uм,n,),
то для установления условия подобия необходимо найти взаимосвязь между масштабами перечисленных физических величин:
m1 = uм,1/ UH,1; m2 = uм,2/ UH,2 и т. д.
Значения всех указанных масштабов не могут быть приняты произвольно; это можно показать на простейшем примере геометрического подобия. Например, можно произвольно назначить линейный масштаб двух геометрических фигур; однако, если фигуры подобны, то масштаб углов всегда равен единице. Физическое подобие явлений, протекающих в натуре и модели, обеспечивается только при определенной взаимосвязи между значениями масштабов физических величин. Чтобы назначить эти масштабы и установить взаимосвязь между ними, необходимо определить критерии подобия.
Существует два способа получения критериев подобия: анализ размерностей и критериальный анализ уравнений, которые в самом общем виде описывают изучаемое явление. Первый способ применяется для явлений мало изученных, для которых можно составить лишь перечень определяющих эти явления физических величин. Для большинства задач строительной механики успешно реализуется второй способ, так как для таких задач составлены системы уравнений, описывающих поведение изучаемого объекта при заданных воздействиях и граничных условиях. В этом случае условия моделирования могут быть получены наиболее корректным способом — методом анализа уравнений.
Если для механической системы известна совокупность определяющих ее физических величин, то для получения условий подобия необходимо из этих величин составить безразмерные комплексы. При этом сочетание группы физических величин, образующих безразмерный степенной комплекс, называется критерием подобия и обозначается π. Первая теорема подобия гласит: подобные явления характеризуются численно одинаковыми критериями подобия. Из этого следует, что безразмерные комплексы πi (i=1, 2, 3,...), составленные из параметров натурной конструкции и из соответственных параметров ее модели, численно равны, например,
π1=σнЕн-1=σмЕм-1; π2=Рнσн-1lн-2= Рмσм-1lм-2и т. д.
Как составить такие безразмерные комплексы и сколько их необходимо для того, чтобы полностью охарактеризовать подобие натуры и модели,— это можно выяснить из второй теоремы подобия (π -теоремы). Если явление описывается n-размерными величинами, из которых k имеет независимые размерности, то функциональная зависимость между характеризующими явление величинами
x1=F(x2, x3,... xk,..., хп)
может быть представлена в виде зависимости между безразмерными комплексами:
π1=f(π2, π3,..., πn-k).
Кроме того, если среди определяющих явление величин имеются безразмерные параметры, то они также служат критериями подобия.
При составлении критериев подобия с помощью анализа размерности обычно исходят из того, что все члены любого физического уравнения, представленного в форме многочлена, имеют одинаковую размерность. Существует несколько приемов, позволяющих формализовать процедуру компоновки безразмерных комплексов. В качестве примера рассмотрим прием исследования на модели распределения напряжений в стержне, выполненном из вязкоупругого материала, при воздействии на его торцы импульсного растяжения. При составлении математической модели можно предположить, что распределение напряжений σ в сечениях участка l вдоль оси стержня зависит от уровня деформации ε, от скорости деформирования έ, от характеристик упругости Е и вязкости η материала. Функциональной связью между перечисленными величинами
σ = φ(ε,έ,E,η, l)
можно задаться, например, в виде степенного одночлена
σ = εpέmErηs l t
Здесь р, т, r, s, t — произвольно выбранные показатели степени, значения которых можно определить из условия равенства размерности левой и правой части выражения. С этой целью произведем в этом выражении замену физических символов обозначениями их размерностей:
[ML-1Т-2] = [Т-1] m[ML-1 T-2]r[ML-1 Т-1 ]s [L]t,
где М, L, Т — основные единицы размерности системы единиц (СИ) — масса, длина, время. Безразмерная величина ε в выражение не вводится.
Так как показатели степени при одноименных единицах размерности в левой и правой части выражения должны быть одинаковыми, составим соответствующие уравнения:
[М] 1=r + s;
[L] — 1 = —r—s + t;
[Т] —2 = —m—2r—s.
Система уравнений содержит четыре неизвестных, поэтому решим ее, например, относительно s и подставим полученные показатели степени (r=l—-s; m = s; t = 0) в выражение
σ = έsE1-sηs.
Произведение величин с одинаковыми показателями степени образуют искомые безразмерные комплексы — критерии подобия
π1=σE-1;
π2=έsηsE-s.
Число полученных критериев согласуется с предсказанными π-теоремой, так как размерных величин пять (n = 5), а число независимых размерностей к = 3 и, следовательно п — к = 2. Безразмерная величина ε также служит критерием подобия π3 = ε. Таким образом, полученные безразмерные комплексы π1, π2 и π3 являются для рассматриваемой задачи критериями подобия.
При составлении условий моделирования удобнее пользоваться не критериями подобия, а уравнениями масштабов или индикаторами подобия. Для их получения входящие в критерии подобия физические величины заменяют константами подобия (масштабами).
Очевидно, что для подобных явлений все индикаторы подобия I равны единице
Ii=  ,
,
J=1, 2, …, m.
В рассматриваемом примере индикаторы подобия
I1=σrEr-1=1;
I2=εrsηrsEr-s=1;
определяют условия построения и испытания модели. Согласно индикаторам
I1 и I3 масштаб напряжений равен масштабу модуля упругости, а распределение деформаций в модели и в натуре должно быть одинаковым. Индикатор подобия I2 позволяет установить масштаб скорости деформирования стержня-модели, поскольку выбор материала модели одновременно определяет значение масштабов ηr и Еr.
Метод анализа размерности применяется для установления критериев полного подобия, когда все величины одинаковой размерности моделируются в одном и том же масштабе. Однако в отдельных случаях по этому методу могут быть получены безразмерные комплексы, характеризующие условия приближенного подобия.
Для иллюстрации метода с помощью испытания модели-оболочки определим несущую способность натурной конструкции. Согласно гипотезе А. Р. Ржаницына, верхняя оценка несущей способности Р пологих выпуклых оболочек постоянной толщины (со срединной поверхностью в виде эллиптического параболоида) определяется параметрами
P=f(A, В, h, δ, σ(+), σ(-)),
где А и В — размеры оболочки в плане, h — стрела подъема, δ — толщина оболочки, σ(+) и σ(-) —пределы прочности материала при растяжении и сжатии. Собственный вес оболочки в данном случае не учитывается.
Среди перечисленных в выражении величин независимые размерности имеют, например, А и σ(+); если эти величины использовать в качестве основных, то с их помощью выражение может быть преобразовано в зависимости между безразмерными комплексами вида
Р/А2 σ(+) = φ(В/А, h/ А, δ/A, σ(-) / σ(+)).
Здесь можно выделить 3 группы критериев подобия
π1=P/A2σ(+);
π2=B/A=h/A=δ/A;
π3= σ(-)/σ(+).
Критерий π3 определяет условие выбора материала модели: отношение его прочности при сжатии к прочности при растяжении должно быть таким же, как у материала натурной оболочки. Критерий подобия яг устанавливает требование геометрического подобия в вертикальной и горизонтальной плоскости. Однако практически удовлетворить это требование трудно. При толщине обечайки современных оболочек 4—6 см даже в случае сравнительно крупномасштабной модели (lr ≈1/20) толщина ее скорлупы должна составлять 2— 3 мм, что практически неосуществимо по технологическим причинам. Если же ввести два независимых геометрических масштаба— один для горизонтального Ar = Br = lr, а другой только для вертикального направления (hr = δr), то критериальный комплекс примет вид π1=P/Aδσ(+), индикаторы подобия
I1=Prlrδrσr(+) =1;
I2=(σ(-) / σ(+))r =1
определяют необходимые условия моделирования.
Для конкретизации полученных условий моделирования рассмотрим определенные числовые значения. Пусть размеры натурной оболочки в плане 30X24 м, стрела подъема 5 м, толщина 4 см. Проектный класс бетона В50
(Rпр≈28 МПа); арматура класса А-1 (Rа = 235 МПа), ее диаметр d = 6 мм, шаг армирования и = 20 см. Оборудование позволяет испытать модель с максимальным размером в плане до 1,5 м (lr = 1/20) и толщиной около 1 см (δr=1/4), т. е. для натуры
σн(-)= Rпр = 28МПа;
σн(+) = Raπd2/4δu =235π-0,62/4 * 4*20 = 0,83 МПа;
(σ(-) / σ(+))н = 28/0,83 = 33.
Последнее отношение является единственным технологическим ограничением при изготовлении модели. Выполняя модель из раствора с фактическим Rnp = σм(-) =35,3 МПа и армируя ее проволокой d = 2 мм (Rа = 216 МПа), шаг арматурной сетки определяют из условий
σм(+) = σм(-) /(σ(-) / σ(+))н = 35,3/33 = 1,07 МПа,
откуда
им =(Rаπd2/4δσ(+))м = 216π0,22/4 • 1 • 1,07 = 6,25 см;
σr(+)=0,775.
В соответствии с принятым условием моделирования
Рн = Рмlrδr σr(+)= 62Рм
т. е. несущая способность проектируемой натурной оболочки может быть определена простым пересчетом результатов испытаний ее модели.
Процедуру преобразования алгебраических и дифференциальных уравнений с целью получения индикаторов подобия рассмотрим на конкретных примерах. В частности, для моделирования стержневых упругих систем индикаторы подобия можно получить при преобразовании любого уравнения, устанавливающего связь между действующими усилиями и перемещениями этой системы. Например, уравнения прогибов шарнирно опертой балки, нагруженной равномерно распределенной нагрузкой q:
у= [ql3x/24~qlx3/12 + qx4/24]EI,
где у — прогиб, Е — модуль упругости, l — пролет балки; ось х совпадает с осью балки, и начало координат совмещено с левой опорой; I — момент инерции сечения балки.
Порядок преобразования такого уравнения в индикаторы подобия следующий:
а) физические величины, входящие в уравнение, заменяют масштабами этих величин, при этом показатели степени остаются без изменений, а числовые коэффициенты становятся равными единице;
б) полученные безразмерные отношения приравнивают друг к другу и делят на один из них (знаки, стоящие перед такими комплексами, опускают).
Так, применяя п. а и б к рассматриваемому примеру, получим:
y r =q r l3rx r /Erl r = q r lrx3 r /Erl r = q r x4 r /Erl r
и далее
I1=qr lr3xr/yrErIr = 1;
I2=qr xr3lr/yrErIr = 1;
I3 = qrx4r/yrErIr = 1.
Полученные индикаторы подобия при определенных ограничениях могут быть упрощены. Если принять геометрические маштабы в направлении осей X и У одинаковыми у r = х r = l r, то вместо трех индикаторов подобия достаточно записать лишь один
qrl3rE-1Ir-1 = 1
Заметим, что выражение не требует подобия формы поперечного сечения балок модели и натуры, а только определенного масштаба момента инерции I r — интегральной характеристики сечения. В случае полного геометрического подобия сечений (hr = br = lr) масштаб момента инерции (производный масштаб) может быть заменен основным
I r = b r h r 3 = l4г
и индикатор подобия примет вид
I=qrEr-1lr-1 = 1,
т. е. условие моделирования изогнутой оси геометрически подобных балок, либо любых других стержневых систем, содержит три независимых масштаба, два из которых могут быть выбраны произвольно.
Рассмотрим процедуру получения индикатора подобия при преобразовании физических уравнений, содержащих дифференциальные операторы. Условия подобия явлений, разумеется, не зависят от того, записаны ли они в виде алгебраических или дифференциальных уравнений. Если уравнение содержит дифференциальные операторы, то в процессе замены каждой физической величины соответствующим множителем преобразования знаки дифференциалов следует опустить. Например, коэффициент подобного преобразования уравнения
v = dmy/dxm
примет вид
v r =y r /x rm.
Для оператора Лапласа
 2w =д2w/ дх2 +d2w/dy2
2w =д2w/ дх2 +d2w/dy2
коэффициент подобного преобразования
(  2w) r=wr / х r 2 = wr/y r 2,
2w) r=wr / х r 2 = wr/y r 2,
или при равенстве масштабов xr = yr = lr:
(  2w) r =wr/l2r.
2w) r =wr/l2r.
Аналогично, оператор 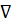 2w можно преобразовать как
2w можно преобразовать как
(  4w) r =wr/lr 4
4w) r =wr/lr 4
Для получения индикаторов подобия (также как и в случае алгебраических уравнений) все найденные из уравнения безразмерные степенные комплексы приравнивают друг к другу и затем делят на один из них. В частности, пусть требуется определить индикаторы подобия для моделирования изогнутой поверхности пластины, для которой известно уравнение функции прогибов
 Aw=p/D,
Aw=p/D,
где w — прогиб, р — интенсивность распределенной по поверхности нагрузки,
D = Eh3/12(1—μ)2
— цилиндрическая жесткость (h — толщина пластины, μ— коэффициент Пуассона). Преобразование такого уравнения дает следующие безразмерные комплексы:
wr/lr4 = pr/Dr;
Dr =Erhr3/(1-μr2).
Если коэффициент Пуассона материалов модели и натуры одинаков (μ r = 1), то Dr = Erhr3 и индикаторами подобия будут
I1=prlr4/wrErhr3=1;
I2 =μr = 1.
Принимая hr = lr, а также полагая, что прогибы малы и геометрическое подобие сохранится, установим wr = hr = lr. Тогда индикаторы подобия примут вид
I1=рrЕr-1 /wrErhr3=1;
I2=μr=1.
Если в выражении и ранее полученном индикаторе подобия производные масштабы внешних сил заменить основными
pr =Prlr-2,
qr = Prlr-1,
где Р r — масштаб сил, то оба выражения окажутся идентичными:
I=Рrlr-2Er-1 = 1.
Таким образом, если для моделирования стержневой системы достаточно было удовлетворить лишь один индикатор подобия, то в случае двух- и трехосного напряженного состояния полное подобие требует выполнения еще одного условия — μ r =1.
Для обеспечения подобия изучаемых явлений необходимо кроме равенства единице индикаторов подобия обеспечить также подобие начальных и граничных условий. Начальные и граничные условия определяют однозначность результатов моделирования. Условия однозначности включают соответствие способа закрепления модели и натуры, заданных на контуре или поверхности сил и перемещений, соответствие предельных соотношений, в рамках которых рассматривается исследуемая расчетная модель. Например, выбор масштаба I r, входящего в индикатор подобия, формально никаких ограничений на форму поперечного сечения не накладывает. Однако по существу масштабы длин в направлении высоты и ширины сечения (hr и b r) не могут быть заданы произвольно, ибо модель должна оставаться простой балкой и не превращаться в балку-стенку или пластину.
При использовании методов моделирования для получения условий подобия рассматриваются следующие исходные уравнения: дифференциальные уравнения равновесия (движения); уравнения совместности деформаций и уравнения связи напряжений и деформаций. При моделировании напряженно деформированного состояния упругих изотропных тел преобразование указанных систем уравнений позволяет получить следующие индикаторы подобия:
I1 = σrEr-1εr-1=1;
I2 = μr=1;
I3 = lrur-1εr=1;
I4 = grρr lr Er-1εr-1=1;
I5 = ρr lr 2Er-1Tr-2=1;
где и r — масштаб перемещений, g r — масштаб ускорения свободного падения, ρr — масштаб плотности, Т r —масштаб времени.
Кроме того, одназначность моделирования определяется следующими граничными условиями:
uk,r ur -1=1;
pr σr -1=1;
где uk,r — масштаб заданных на контуре перемещений, р r — масштаб распределенной поверхностной нагрузки.
При изучении гибких упругих систем необходимо также соблюдать условие
εr=γr=1,
где γr — масштаб деформаций сдвига.
Условия подобия нестационарного температурного поля θ(х, у, z, Т) в однородном изотропном теле можно получить, проводя преобразования уравнения теплопроводности Фурье
сρ д θ /dT = λ(д2 θ /дx2+д2 θ /дy2 + д2 θ /дz2) + q
и уравнения свободного теплообмена поверхности S с окружающей средой
д θ /dS = α θ (θ c — θ)/λ,
где с — удельная теплоемкость материала; λ — теплопроводность; q — плотность внутренних источников тепла, выделяемого ими в единицу объема за единицу времени; α θ — коэффициент теплопередачи между средой и поверхностью тела; θ c — температура окружающей среды.
Условия моделирования температурного поля включают шесть индикаторов подобия:
λ r Тr cr-1 ρr-1lr -2=1; qrlr2λr-1 θ r=1;
θ 0,r θ r=1; θ s,r θ r-1=1;
θ c,r θ r-1=1; αθ rlrλ r-1=1.
Масштабы ρ r, с r, λ r определяются выбором материала модели. Коэффициент теплопередачи зависит от многих факторов и в каждом конкретном случае должен быть получен экспериментально. После того, как установлен масштаб αθ r, геометрический масштаб находят из выражения
lr=αθr-1λr
При исследовании температурных напряжений к ранее полученным индикаторам подобия добавляется еще один
I6 = σrЕr-1αr-1 θ r-1 = 1,
где αr — масштаб температурного коэффициента линейной деформации.
Таким образом, при составлении плана эксперимента и проектировании модели для изучения задачи термоупругости необходимо рассматривать совместно весь комплекс индикаторов подобия, при этом начальные и граничные температурные условия оказываются взаимосвязанными с граничными статическими и кинематическими условиями.
Рассмотренные условия моделирования в рамках полного линейного подобия содержат большой набор индикаторов, предельных соотношений и т. д., одновременное выполнение которых сопряжено со значительными техническими трудностями, либо оказывается вообще невозможным. Поэтому в практике моделирования инженерных конструкций широкое распространение получило приближенное подобие. В отличие от полного подобия, когда все индикаторы подобия, включая масштабы безразмерных величин, равны единице, при приближенном моделировании допускается нарушение соответствия между моделируемым объектом и моделью в части некоторых параметров, если такое искажение подобия не очень существенно для рассматриваемой задачи, либо может быть оценено аналитически или экспериментально. При этом всесторонней оценке неизбежных погрешностей моделирования должно уделяться большое внимание, чтобы не допустить вырождения подобия и получения ошибочных результатов.
Факторы, в отношении которых не соблюдается подобие, могут быть разнообразными: невоспроизведение на модели технологических особенностей соединений и остаточных напряжений в элементах конструкций; различие свойств материалов модели и оригинала, приближенное подобие геометрической формы и распределения действующих усилий (например, от собственного веса), увеличенные по отношению к натуре деформации модели и т. д. Рассмотрим некоторые наиболее распространенные случаи приближенного моделирования.
Моделирование при μr≠1. Учет влияния неодинаковых значений коэффициента Пуассона материалов модели и натуры можно провести несколькими способами. Для плоского напряженного состояния С. Г. Лехницким было предложено изготовлять две модели с существенно разными коэффициентами Пуассона μM1 и μM 2, при этом масштабы геометрического и силового подобия моделей могут быть любыми. Напряжение в натурном объекте σн определяется как разность экспериментально полученных напряжений σM1 и σM 2 в сходственных точках каждой модели, компоненты которых умножены на соответствующие корректирующие коэффициенты и константы подобия. Например, в частном случае обобщенного плоско-напряженного состояния, когда натура и обе модели геометрически тождественны, масштаб сил рr=1,
σн = σм1(μн — μм2) /(μм1 — μм2)- σм2(μн — μм1) /(μм1 — μм2).
Одним из распространенных приемов оценки погрешностей моделирования, обусловленных различием коэффициента Пуассона материалов модели и натуры, является построение функций влияния выражений, входящих в решения задач теории упругости: l+μ; 1—μ2; μ/(1—μ); 1—2μ и др. Такие функции влияния позволяют для определенного диапазона соотношений компонентов деформаций (ε2/ε1, ε3/ε1) оценивать масштаб выражений, содержащих μ. Например, анализ масштаба (1 — μ2)r в уравнении изгиба пластинок, защемленных или шарнирно опертых по контуру, показал, что при исследовании стальной пластины (μн = 0,28) на модели из органического стекла (μм = 0,36) погрешность определения напряжений может достигать 30%, а при коэффициенте Пуассона модели μм = 0,5 до 80%.
Наибольшие погрешности приближенного моделирования в отношении невыполнения условия μr=1 следует ожидать в тех областях исследуемого объекта, где велико среднее напряжение σср. Прежде всего это относится к трехмерному растяжению, возникающему вблизи концентраторов напряжений (отверстий, надрезов) в растянутых толстостенных элементах.
В том случае, когда технологические трудности не позволяют воспроизводить в модели поперечное сечение требуемой формы и размеров, как это имело место при моделировании несущей способности оболочки, либо, когда для повышения точности измерений необходимо увеличить деформации модели, приходится использовать геометрически аффинное подобие. Следует, однако, иметь в виду, что полное геометрическое подобие становится совершенно обязательным, например, при исследовании устойчивости элементов конструкций.
При необходимости аффинного преобразования формы сечения упругой пластины связь между масштабами длин в направлении координатных осей и масштабом деформации εr можно получить с помощью преобразования следующих уравнений;
εx=— zd2w/dx2; εу = —zd2w/dy2;
γxy = — 2zd2w/dxdy.
Если масштабы в направлении осей x и у (в плоскости пластины) равны xr = yr = lr и, следовательно, εx ,r = εy ,r = γxy, r=εr, то с учетом того, то zr = wr = hr, выражение преобразуется к виду
εr= zr wr/lr2= hr2/l r2
где hr — масштаб толщины пластины.
Обычно по техническим причинам бывает необходимо увеличить масштаб в направлении толщины пластины hr> l r; при этом соответственно увеличиваются масштабы εr > 1 и wr> 1. Такое увеличение деформаций и перемещений элементов модели позволяет повысить точность измерения этих параметров. При моделировании статически определимых систем увеличение масштаба деформаций εr > 1 вполне допустимо при условии, если за счет увеличенных перемещений не возникнут дополнительные связи, превращающие систему в статически неопределимую.
Приближенное подобие сил тяжести. Если модель и натура выполнены из одинакового материала, то согласно I4 = grρrlrEr-1 εr-1, полное подобие напряжений, вызванных действием собственного веса, реализуется лишь при lr =1, т. е. невозможно даже масштабное моделирование.
Подобие распределения деформаций в модели и натуре (εr — 1) выполняется при
lr = Еr/ γr,
где γr =grρr — масштаб объемного веса соответствующих материалов.
Следовательно, выбор материала модели (Е/ γ) r одновременно определяет и требуемый геометрический масштаб модели. Например, при исследовании стальной конструкции с помощью модели, выполненной из органического стекла, масштаб (Е/ γ) r≈ 1/10—1/15; таким же должен быть и геометрический масштаб, если необходимо обеспечить подобие распределения деформаций. В случае, когда требуется увеличить масштаб деформаций, чтобы повысить точность их измерения, стремятся подобрать для модели более низкомодульный материал, либо увеличить геометрический масштаб (например, до 1/5 вместо указанного выше 1/10—1/15). Если необходимо изготовить модель из того же материала, что и натура, или когда нет возможности выполнить ее в требуемом геометрическом масштабе, увеличивают силу тяжести путем центрифугирования модели или дополнительный собственный вес создают соответствующим образом распределенными внешними нагрузками.
Если целью испытаний является моделирование только напряженного состояния сооружения от действия собственного веса, то плотность материала модели должна быть увеличена обратно пропорционально ее геометрическому масштабу
lr = γr-1.
Для увеличения массы цементного раствора или гипса в качестве заполнителя используют свинцовую дробь.
При проведении исследований за пределами упругости модель следует, по возможности, изготовить из того же материала, что и натурную конструкцию. В этом случае неполное подобие напряженного состояния может быть обусловлено только масштабным эффектом. Природу масштабного эффекта связывают с технологическими факторами, поскольку они по-разному влияют на однородность и механические свойства материала в зависимости от формы и размеров сечений, а также с запасом упругой энергии, накопленной в деформируемой системе. Эта энергия, естественно, возрастает с увеличением размеров конструкции и способствует более быстрому протеканию реологических процессов.
Согласно статистическим гипотезам в теле имеется большое число дефектов различной степени опасности, которые подчиняются некоторому распределению. Чем крупнее тело, тем больше вероятность обнаружить первичный элемент низкой прочности и тем ниже прочность тела в целом. Следовательно, с помощью статистических гипотез можно объяснить лишь влияние масштабного эффекта на прочность хрупких тел, но не на их напряженное состояние.
В упругопластической стадии деформирования увеличение размеров геометрически подобных элементов, выполненных из одинакового материала и нагруженных с соблюдением условий подобия, приводит к изменению характера напряженного состояния и к непропорциональному (σr/lr≠1) преобразованию градиентов напряжений. С увеличением масштаба модели влияние всех перечисленных факторов снижается и, начиная с какого-то предела, становится несущественным. Поэтому при моделировании работы конструкций в упругопластической стадии деформирования при выборе масштаба модели необходимо обязательно проводить оценку влияния рассмотренных факторов.
Если при моделировании напряженного состояния конструкций в неупругой области материал модели отличается от натурного, то комплекс индикаторов подобия оказывается уже недостаточным. Введение дополнительных условий моделирования существенно затрудняет проведение таких исследований.
Сравнительно просто осуществляется моделирование лишь в частном случае, когда характер диаграмм «σ— ε» деформирования материалов модели и натуры соответствует схеме Прандтля. В этом случае за пределами пропорциональности μr= 1 (поскольку для материалов и натуры, и модели μ = 0,5) масштаб напряжений равен масштабу пределов пропорциональности этих материалов — (σпц)r.
Кроме подобия диаграмм «σ— ε» нужно отметить еще две особенности моделирования в неупругой области. Во-первых, масштаб напряжений — переменная величина, определяемая для каждой исследуемой точки конструкции с помощью принятой диаграммы деформирования. Во-вторых, за пределами упругости коэффициент поперечной деформации μ также величина переменная. Поэтому условие μr= 1 реализуется лишь при полной идентичности зависимостей μ — ε, построенных для материалов модели и натуры. Удовлетворить это условие обычно не удается. В последние годы разрабатываются специальные модельные полимерные материалы (поликарбонат и др.), диаграммы деформирования которых подобны определенным металлическим сплавам.
Дата публикования: 2015-07-22; Прочитано: 873 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
