 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вычисление объемов тел
|
|
1. Вычислить объем пирамиды с высотой Н и площадью основания S0 (рис. 7)

Решение. Вершину пирамиды S примем за начало координат и направим ось Ох по высоте Н пирамиды от вершины к основанию. Рассечем пирамиду плоскостью, параллельной основанию и отстоящей от вершины S на расстоянии х, 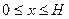 . Площадь этого сечения зависит от х, и мы обозначим ее через S(x). Пользуясь известным свойством сечений пирамиды, параллельных основанию, составляем пропорцию.
. Площадь этого сечения зависит от х, и мы обозначим ее через S(x). Пользуясь известным свойством сечений пирамиды, параллельных основанию, составляем пропорцию.
|
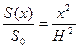 , откуда
, откуда  .
.
Объем пирамиды равен
 .
.
2. Определить объем сегмента параболоида вращения.
Решение. Пусть уравнение параболы, вращение которой вокруг оси Оx дает данный параболоид, будет 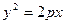 . Обозначим: h - высота сегмента параболоида вращения, r - радиус основания сегмента, х - расстояние плоскости, параллельной основанию сегмента от вершины параболы вращения, а ρ- радиус окружности, получающейся в сечении параболоида вращения указанной плоскостью. Тогда
. Обозначим: h - высота сегмента параболоида вращения, r - радиус основания сегмента, х - расстояние плоскости, параллельной основанию сегмента от вершины параболы вращения, а ρ- радиус окружности, получающейся в сечении параболоида вращения указанной плоскостью. Тогда 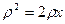 , а площадь S(x) указанного сечения равна S(x)=
, а площадь S(x) указанного сечения равна S(x)=  Объем Vh сегмента параболоида вращения равен:
Объем Vh сегмента параболоида вращения равен:
 .
.
Площадь S основания сегмента равна  и так как
и так как 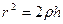 , то
, то 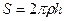 . Отсюда
. Отсюда 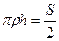 , и формулу для объема сегмента можно записать так:
, и формулу для объема сегмента можно записать так:
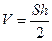 ,
,
т.е. объем сегмента параболоида вращения равен половине произведения площади основания сегмента на его высоту.
3. Вычислить объема тела, образованного вращением вокруг оси Ох площади, ограниченной параболой 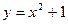 и прямой у=3х-1.
и прямой у=3х-1.
Решение. Тело образовано вращением площади, ограниченной заданными кривыми (рис. 8) вокруг оси Ох.
|

Чтобы найти абсциссы точек пересечения кривых решаем систему уравнений:
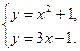
Отсюда х1=1, х2=2. В нашем случае 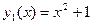 и
и 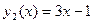 . Следовательно, имеем:
. Следовательно, имеем:
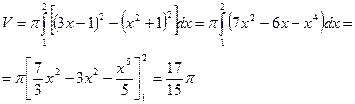
Рис.8
4. Вычислить объем тора. Тором называется тело, получающееся при вращении круга радиуса а вокруг оси, лежащей в его плоскости на расстоянии b от центра 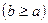 (форму тора имеет, например, баранка).
(форму тора имеет, например, баранка).
Решение. Пусть круг вращается вокруг прямой AE (рис. 9). Тогда объем тора может быть рассмотрен как разность объемов вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Оу.

|
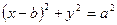 ,
,
откуда 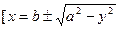 , причем уравнение кривой BCD
, причем уравнение кривой BCD 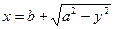 , а уравнение кривой BCD
, а уравнение кривой BCD 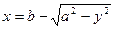 .
.
Следовательно, искомый объем равен:
Рис.9
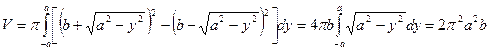 .
.
5. Вычислить объем тела, которое образуется при вращении одной арки циклоиды 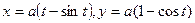 вокруг оси абсцисс.
вокруг оси абсцисс.
Решение. В формуле
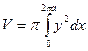
Делаем замену переменной, полагая  . Когда х изменяется от 0 до 2πа, t изменяется от 0 до 2π:
. Когда х изменяется от 0 до 2πа, t изменяется от 0 до 2π:
 .
.
6. Найти объем тела, образованного вращением вокруг полярной фигуры, ограниченной этой осью и дугой логарифмической спирали 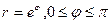 .
.
Решение. Преобразуем уравнение кривой к параметрическому виду
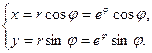
Мы имеем 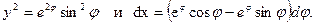
Поэтому
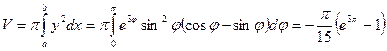 .
.
Мы получили отрицательное значение V, так как значению φ=0 соответствует точка (1;0), а значению π – точка N 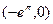 , лежащая левее точки M. Итак,
, лежащая левее точки M. Итак,
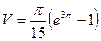 .
.
Дата публикования: 2015-07-22; Прочитано: 486 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
