Свойство монотонности

VII. Если подынтегральная функция определенного интеграла непрерывна и неотрицательна, а верхний предел интегрирования больше нижнего или равен ему, то определенный интеграл также неотрицателен.

В самом деле, пусть f(x)≥0 при a ≤ x ≤ b. Так как F`(x)= f(x)≥0, то первообразная F(x) есть возрастающая функция (точнее, неубывающая функция). В таком случае при b≥a имеем

.

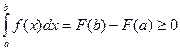VIII. Неравенство между непрерывными функциями можно интегрировать почленно при условии, что верхний предел интегрирования больше нижнего.

Действительно, пусть f(x)≤g(x) a ≤ x ≤ b, где f(x), g(x) непрерывны на отрезке [a,b]. Так как g(x)- f(x) ≥0, то при b≥а в силу свойств VI, VII имеем

,

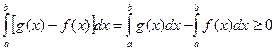отсюда

.

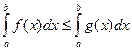Замечание. Пусть f(x) – знакопеременная непрерывная функция на отрезке [a,b], где b≥а. Например (рис. З), f(x)≤0 при a ≤ x ≤ α, f(x)>0 при α ≤ x ≤ β и f(x)≤0 при β ≤ x ≤ b.

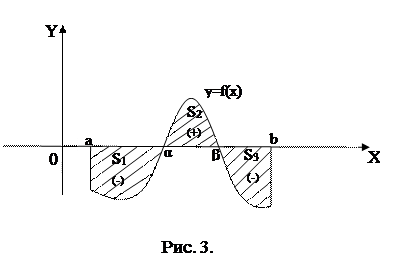В силу свойства аддитивности VI, учитывая геометрический смысл интеграла, имеем

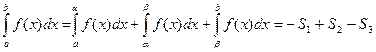, (5)

где S₁, S₂, S₃ – площади соответствующих криволинейных трапеций.

Таким образом, определенный интеграл, в общем случае, при a<b представляет собой алгебраическую сумму площадей соответствующих криволинейных трапеций, где площади трапеций, расположенных выше оси Ох, берутся со знаком плюс, а площади трапеций, расположенных ниже оси Ох, - со знаком минус.

Если b < a, то обстоит наоборот.

Заметим, что площадь заштрихованной на рис. № фигуры выражается интегралом

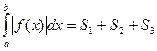(b < a).