 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Краткие сведения из теории. Методические указания к лабораторной работе
|
|
ИЗУЧЕНИЕ МЕТОДОВ ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ И КРИТЕРИЕВ СОГЛАСИЯ
Методические указания к лабораторной работе
Нижний Новгород 1999
Составители: Д.В.Ломакин, А.В.Семашко
УДК 621.396.096
Изучение методов проверки статистических гипотез и критериев согласия: Метод. указания к лаб. работе/НГТУ; Сост.: Д.В.Ломакин, А.В.Семашко. Н.Новгород, 1999.
Приведен теоретический материал, освещающий проблему оценки правдоподобности гипотез о законах распределения случайных величин и оценки соответствующих параметров. Рассматриваются наиболее употребительные в настоящее время критерии согласия. Даны методические указания по выполнению лабораторной работы, приведены контрольные вопросы и список рекомендованной литературы.
Редактор И.И.Морозова
Подп. к печ. 31.05.99. Формат 60х841/16. Бумага газетная. Печать
офсетная. Печ. л. 1,25. Уч.-изд.л. 0,9. Тираж 300 экз. Заказ 321.
__________________________________________________________________
Нижегородский государственный технический университет.
Типография НГТУ. 603600, Н.Новгород ул.Минина, 24.
Ó Нижегородский государственный
технический университет, 1999
ЦЕЛЬ РАБОТЫ
Изучение методов проверки статистических гипотез, составление соответствующих алгоритмов и анализ их работы методом статистического моделирования на ПЭВМ.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Гипотеза - это предположение об истинности выдвинутого утверждения (суждения). Истинность утверждения (гипотеза) проверяется чаще всего экспериментально. Например, гипотезу “поезд отправляется в 23 часа” можно проверить, прибыв на вокзал к 23 часам. Эта проверка является достоверной. Однако в большинстве случаев полученная в результате эксперимента информация позволяет судить об истинности гипотезы только с некоторой вероятностью. Поскольку мы рассматриваем задачу принятия решения об истинности гипотезы в рамках теории вероятностей, то класс гипотез, которые могут быть выдвинуты, ограничивается моделью теории вероятностей. Модель основного объекта, который изучает теория вероятностей, представляет собой случайную величину, т.е. множество возможных значений с заданной на нем вероятностной мерой. Поэтому гипотеза задается в виде определенного закона распределения случайной величины, а решение об истинности гипотезы выносится на основании информации, которую доставляет выборка 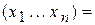 x, т. е. требуется решить, принадлежит выборка гипотетическому (теоретическому) закону распределения или нет. Такие гипотезы называются статистическими.
x, т. е. требуется решить, принадлежит выборка гипотетическому (теоретическому) закону распределения или нет. Такие гипотезы называются статистическими.
Формализуем постановку задачи:
1. Имеется выборка x = 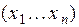 , представляющая собой n реализаций случайных величин x i,
, представляющая собой n реализаций случайных величин x i, 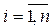 . Числа
. Числа 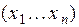 обычно представляют собой результаты некоторого эксперимента (измерения). Предполагается, что все n раз эксперимент проводился в одних и тех же условиях (с точки зрения теории вероятностей), т.е. предполагается, что случайные величины x 1,..., x n имеют один и тот же закон распределения вероятностей
обычно представляют собой результаты некоторого эксперимента (измерения). Предполагается, что все n раз эксперимент проводился в одних и тех же условиях (с точки зрения теории вероятностей), т.е. предполагается, что случайные величины x 1,..., x n имеют один и тот же закон распределения вероятностей 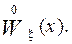 Закон
Закон 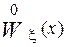 является истинным, но в рамках решаемой задачи неизвестен и подлежит оценке. Термин “оценка” имеет 2 значения. Первое отражает процесс оценивания, а второе - результат
является истинным, но в рамках решаемой задачи неизвестен и подлежит оценке. Термин “оценка” имеет 2 значения. Первое отражает процесс оценивания, а второе - результат
2. Задача исследователя состоит в определении закона 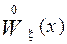 .
.
3. Исходя из каких-либо предположений (физических, интуитивных и проч.) выносится предположение о законе распределения 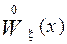 , а именно выдвигается гипотеза Н: случайные величины x распределены по закону
, а именно выдвигается гипотеза Н: случайные величины x распределены по закону 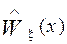 .
.
4. Используя выборку 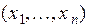 - (результаты опыта), оценивается вероятность истинности выдвинутой гипотезы.
- (результаты опыта), оценивается вероятность истинности выдвинутой гипотезы.
Гипотеза называется простой, если гипотетический (теоретический) закон полностью задан. Иногда ограничиваются проверкой гипотезы о том, что выборка 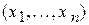 = x принадлежит хотя бы одному из законов распределения данного класса. Такие гипотезы называются сложными, поскольку они состоят из простых гипотез. Например, гипотеза о том, что выборка принадлежит нормальному закону распределения, безразлично с каким средним и дисперсией, является сложной. В частности, гипотезы о неизвестном параметре
= x принадлежит хотя бы одному из законов распределения данного класса. Такие гипотезы называются сложными, поскольку они состоят из простых гипотез. Например, гипотеза о том, что выборка принадлежит нормальному закону распределения, безразлично с каким средним и дисперсией, является сложной. В частности, гипотезы о неизвестном параметре 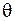 некоторого закона распределения могут быть простыми и сложными. Простая гипотеза утверждает, что параметр
некоторого закона распределения могут быть простыми и сложными. Простая гипотеза утверждает, что параметр 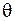 имеет одно конкретное значение
имеет одно конкретное значение  , а сложная гипотеза утверждает, что параметр
, а сложная гипотеза утверждает, что параметр 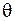 имеет значение, принадлежащее некоторому множеству значений. Приведенные рассуждения показывают, что нет принципиальной разницы между проверкой гипотез и оценкой параметров.
имеет значение, принадлежащее некоторому множеству значений. Приведенные рассуждения показывают, что нет принципиальной разницы между проверкой гипотез и оценкой параметров.
Сформулируем задачу проверки m + 1 простых гипотез. Пусть известно, что выборка c вероятностью, равной единице, принадлежит одному из m + 1 распределений 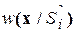 , i=0, 1,..., m, где
, i=0, 1,..., m, где 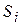 - состояние комплекса условий при котором получена выборка, причем, состояние
- состояние комплекса условий при котором получена выборка, причем, состояние 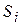 полностью определяет вид распределения
полностью определяет вид распределения 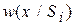 . Состояния образуют полную группу событий с вероятностями P0,...,
. Состояния образуют полную группу событий с вероятностями P0,..., 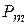
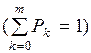 . Гипотеза
. Гипотеза 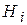 состоит в том, что
состоит в том, что  . Решения
. Решения 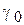 ,...,
,...,  , которые могут быть приняты в пользу соответствующих гипотез
, которые могут быть приняты в пользу соответствующих гипотез 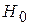 ,...,
,..., 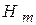 также образуют полную группу событий.
также образуют полную группу событий.
Задача состоит в том, чтобы по заданному показателю качества построить оптимальное правило принятия решения 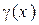 , согласно которому каждой возможной выборке x ставится в соответствие одно из решений. Это означает, что пространство выборок X должно быть разделено на m + 1 непересекающихся областей
, согласно которому каждой возможной выборке x ставится в соответствие одно из решений. Это означает, что пространство выборок X должно быть разделено на m + 1 непересекающихся областей 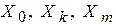 , каждой из которых ставится в соответствие одно из решений
, каждой из которых ставится в соответствие одно из решений  . Следует отметить, что правило
. Следует отметить, что правило 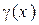 строится до наблюдения выборки x. Правило
строится до наблюдения выборки x. Правило 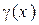 , по которому каждой области
, по которому каждой области 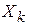 всегда ставится в соответствие определенное решение
всегда ставится в соответствие определенное решение 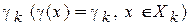 называется детерминированным или нерандомизированным (Рис. 1). Правило
называется детерминированным или нерандомизированным (Рис. 1). Правило 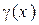 называется рандомизированным, если при попадании x в данную область
называется рандомизированным, если при попадании x в данную область
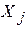 допускается выбор одного из нескольких решений в соответствии с некоторым распределением вероятностей.
допускается выбор одного из нескольких решений в соответствии с некоторым распределением вероятностей.
¡0 ¡1
C1
C0
¡3
C2 C3
¡2
Рис. 1. Разделение пространства х на 4 области (m=3),
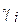 - решение в пользу гипотезы
- решение в пользу гипотезы 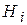
Рассмотрим более подробно случай двух гипотез (m=1)
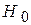 :
: 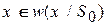 ,
,
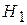 :
: 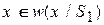 .
.
Гипотезу 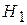 часто называют альтернативной гипотезой или просто альтернативой.
часто называют альтернативной гипотезой или просто альтернативой.
Решение 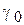 - принятие гипотезы
- принятие гипотезы 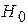 ,
,
решение 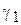 - принятие гипотезы
- принятие гипотезы 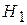 .
.
На практике часто встречается задача, когда 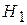 :
: 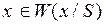 , т.е. гипотеза состоит в выдвижении какого-либо предположения (в данном случае
, т.е. гипотеза состоит в выдвижении какого-либо предположения (в данном случае 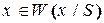 , а альтернатива в отклонении (не подтверждении) этого предположения (
, а альтернатива в отклонении (не подтверждении) этого предположения (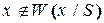 )
)
Правило принятия решения эквивалентно разделению n -мерного пространства выборок X на две непересекающихся области 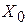 и
и 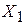 (рис.2). Если
(рис.2). Если 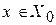 , то принимается решение
, то принимается решение 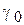 , если
, если 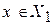 , то принимается решение
, то принимается решение 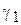 . Область
. Область 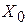 принятия гипотезы
принятия гипотезы 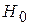 называется допустимой. Область
называется допустимой. Область 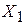 отклонения гипотезы
отклонения гипотезы 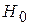 называется критической.
называется критической.
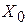
допустимая 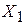
область критическая
область
Рис.2. Разбиение пространства Х на две области (m =1).
В процессе принятия решения могут возникнуть ошибки, которые удобно изобразить в виде следующей диаграммы
1-a
q 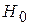 · ·
· · 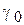 :
: 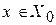
a
b
p=1-q 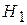 · ·
· · 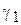 :
: 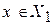 ,
,
1-b
где q - априорная вероятность гипотезы 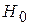 , p - априорная вероятность гипотезы
, p - априорная вероятность гипотезы 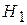 ;
;
a- вероятность ошибки первого рода или уровень значимости, т. е. вероятность отклонения гипотезы 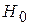 , когда она истинна;
, когда она истинна;
b - вероятность ошибки второго рода, т. е. вероятность принятия гипотезы 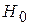 , когда она ложна;
, когда она ложна;
1-b - мощность правила принятия решения.
По формуле полной вероятности можно вычислить безусловные вероятности
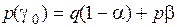 ,
,
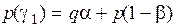 .
.
Перейдем к построению правила выбора решения 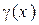 (т.е. решающей схемы или способа разбиения пространства выборок X на допустимую
(т.е. решающей схемы или способа разбиения пространства выборок X на допустимую 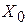 и критическую
и критическую 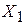 области), которое будем считать оптимальным, если оно обеспечивает минимум средней вероятности ошибки (максимум вероятности правильного принятия решения). Этот критерий качества принятия (выбора) решения был предложен В.А.Котельниковым и назван критерием идеального наблюдателя, а приемник, работающий в соответствии с этим правилом, В.А.Котельников назвал идеальным.
области), которое будем считать оптимальным, если оно обеспечивает минимум средней вероятности ошибки (максимум вероятности правильного принятия решения). Этот критерий качества принятия (выбора) решения был предложен В.А.Котельниковым и назван критерием идеального наблюдателя, а приемник, работающий в соответствии с этим правилом, В.А.Котельников назвал идеальным.
В математической литературе правило выборарешения часто называют критерием. Можно показать, что средняя вероятность ошибки будет минимальна, если решение выносить в пользу гипотезы, имеющей наибольшую апостериорную вероятность 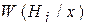 при заданной выборке
при заданной выборке 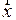 . В нашем случае апостериорные вероятности для
. В нашем случае апостериорные вероятности для 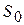 и
и 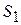 , что то же самое для
, что то же самое для 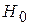 и
и 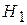 , можно представить в виде
, можно представить в виде
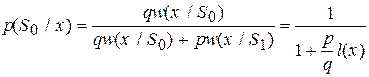
 ,
,
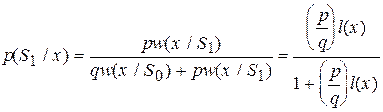 ,
,
где 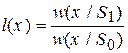 - отношение правдоподобия.
- отношение правдоподобия.
Вывод представленных равенств становится более наглядным, если воспользоваться диаграммой вероятностных переходов (рис.3).
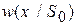
q S0,(H0) · · x
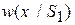
p S1,(H1) ·
Рис. 3
Безусловная вероятность появления некоторой выборки x вычисляется по формуле полной вероятности:
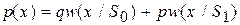 ,
,
а апостериорные вероятности 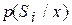 (i =1, 2) по формуле Байеса:
(i =1, 2) по формуле Байеса:
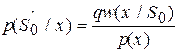 ,
,
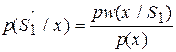 ,
,
где 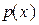 нужно заменить на полученное выше выражение.
нужно заменить на полученное выше выражение.
Теперь можно сформулировать правило выбора решения: принимается гипотеза H1 (отвергается гипотеза H0), если для наблюдаемой выборки x выполняется неравенство
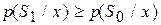
и принимается гипотеза H0 (отвергается гипотеза H1), если
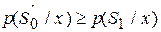 .
.
Для сравнения апостериорных вероятностей можно взять их отношение
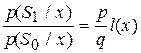 .
.
Тогда условие принятия гипотезы H1 можно записать в виде:
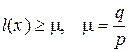 .
.
Таким образом, максимуму апостериорной вероятности соответствует такая критическая область пространства выборок, точки (x) которой удовлетворяют полученному неравенству. Вероятности p и q учитывают априорные сведения о гипотезах. Если гипотезы равновероятны, то m =1 и правило выбора решения сводится к проверке неравенства 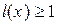 для полученной выборки x.
для полученной выборки x.
Это правило называется правилом максимального правдоподобия и часто используется, когда вероятности гипотез неизвестны, т.е. гипотезы считаются равновероятными.
Принятие решения по правилу максимального правдоподобия совпадает с правилом максимума апостериорной вероятности удовлетворяющим критерию идеального наблюдателя, когда p=q. Итак, если для наблюдаемой выборки x выполняется неравенство
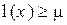 ,
,
то принимается решение g1 (отвергается гипотеза 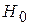 ) и принимается решение g0 (гипотеза
) и принимается решение g0 (гипотеза 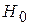 считается истинной) в противном случае. Скалярная величина
считается истинной) в противном случае. Скалярная величина 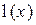 , которая ставится в соответствие каждой выборке
, которая ставится в соответствие каждой выборке 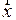 , называется пороговой статистикой. Выборки x, которые удовлетворяют неравенству
, называется пороговой статистикой. Выборки x, которые удовлетворяют неравенству 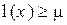 , образуют критическую область X 1 данного правила выбора решения. Для вычисления вероятности ошибки первого рода
, образуют критическую область X 1 данного правила выбора решения. Для вычисления вероятности ошибки первого рода
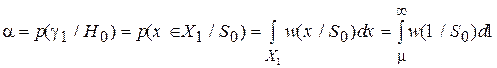 ,
,
которая равна вероятности того, что случайная величина 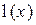 превысит порог m, необходимо знать ее условный закон распределения w(
превысит порог m, необходимо знать ее условный закон распределения w( 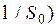 , который не всегда удается легко установить.
, который не всегда удается легко установить.
Аналогично вычисляется вероятность ошибки второго рода:
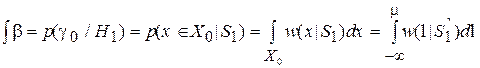
Можно доказать, что правило принятия решения, основанное на вычислении отношения правдоподобия, обеспечивает минимум средней (полной, безусловной) вероятности ошибки, которая равна
 .
.
Часто принятие гипотез основано на другом критерии - критерии Неймана -Пирсона, согласно которому правило выбора решения строится таким образом, чтобы обеспечить минимально возможную величину вероятности ошибки второго рода b при условии, что вероятность ошибки первого рода не больше заданной величины a. Иначе говоря, это правило имеет наибольшую мощность (1-b) среди всех других правил, для которых уровень значимости не превосходит a. Критерий Неймана - Пирсона широко используется в радиолокации, в пожарном деле и проч., где a принято называть вероятностью ложной тревоги, а (1-b) - вероятностью правильного обнаружения (цели, пожара...).
Пороговой статистикой критерия Неймана - Пирсона также является отношение правдоподобия 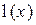 , которое сравнивается с некоторым пороговым значением С. Величина С выбирается таким образом, чтобы вероятность ее превышения пороговой статистикой
, которое сравнивается с некоторым пороговым значением С. Величина С выбирается таким образом, чтобы вероятность ее превышения пороговой статистикой 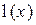 (вероятность выполнения неравенства
(вероятность выполнения неравенства 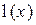 > С) не превышала заданное значение a.
> С) не превышала заданное значение a.
Таким образом, в случае простых гипотез Н0 и Н1 (альтернатива) алгоритм выбора решения сводится к вычислению отношения правдоподобия и сравнению его значения с порогом С.
Задача значительно усложняется, когда хотя бы одна из гипотез является сложной. Например, для проверки простой гипотезы Н0 о том, что случайная величина имеет заданный (гипотетический) закон распределения против сложной альтернативы Н1, о которой ничего не известно, разработаны специальные критерии, которые называются критериями согласия. Эти критерии позволяют судить, насколько экспериментальные данные согласуются с предполагаемым (теоретическим, гипотетическим) законом распределения (гипотезой Н0 ).
Самым простым методом оценки является визуальное сравнение гистограммы, полученной по выборке x, и гипотетического закона распределения 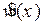 . Однако этот метод является очень грубым, субъективным, не имеет четкой количественной характеристики и поэтому не может быть использован как критерий в строгих научных исследованиях. Его рекомендуется применять в качестве основы для выдвижения гипотез. Рассмотрим некоторые другие критерии, которые широко используются в настоящее время.
. Однако этот метод является очень грубым, субъективным, не имеет четкой количественной характеристики и поэтому не может быть использован как критерий в строгих научных исследованиях. Его рекомендуется применять в качестве основы для выдвижения гипотез. Рассмотрим некоторые другие критерии, которые широко используются в настоящее время.
Критерий согласия Колмогорова основан на проверке близости между эмпирической (выборочной) функцией распределения - 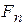 (x) и гипотетической функцией распределения - F(x). В данном случае гипотеза Н0 предполагает, что истинная функция распределения G(x) равна гипотетической функции распределения F(x):
(x) и гипотетической функцией распределения - F(x). В данном случае гипотеза Н0 предполагает, что истинная функция распределения G(x) равна гипотетической функции распределения F(x):
H0: G(x)=F(x).
Для количественного выражения сходства функций 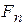 (x) и F(x) используется статистика Колмогорова:
(x) и F(x) используется статистика Колмогорова:
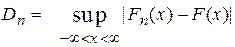 .
. 
Функция 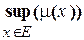 означает нижнюю грань функции m(x) на допустимом множестве аргумента x Î E.
означает нижнюю грань функции m(x) на допустимом множестве аргумента x Î E.
Очевидно, что 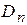 - случайная величина, поскольку ее значение зависит от случайной функции
- случайная величина, поскольку ее значение зависит от случайной функции 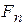 (x). Если гипотеза Н0 справедлива, то при неограниченном возрастании n функция
(x). Если гипотеза Н0 справедлива, то при неограниченном возрастании n функция 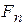 (x)®F(x) при всяком x и
(x)®F(x) при всяком x и 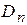 ®0. Если же гипотеза Н0 не верна, то
®0. Если же гипотеза Н0 не верна, то 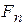 (x)®G(x) и G(x)¹F(x), а
(x)®G(x) и G(x)¹F(x), а 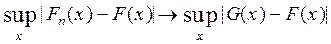 . Последняя величина положительна, так как G(x) не совпадает с F(x).
. Последняя величина положительна, так как G(x) не совпадает с F(x).
Отсюда следует, что величина Dn имеет тенденцию к увеличению с ростом степени различия между истинной функцией распределения G(x) и гипотетической функцией распределения F(x). Это свойство позволяет использовать 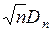 в качестве пороговой статистики критерия. Поскольку
в качестве пороговой статистики критерия. Поскольку 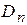 ® 0 при истинности гипотезы Н0, то для стабилизации закона распределения пороговой статистики
® 0 при истинности гипотезы Н0, то для стабилизации закона распределения пороговой статистики 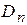 умножается на неограниченно растущую величину
умножается на неограниченно растущую величину 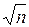 . Случайная величина
. Случайная величина 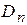 обладает замечательным свойством, которое заключается в том, что её закон распределения оказывается одним и тем же для всех непрерывных функций G(x). Он зависит только от объема выборки n. Доказательство этого факта основано на том, что статистика
обладает замечательным свойством, которое заключается в том, что её закон распределения оказывается одним и тем же для всех непрерывных функций G(x). Он зависит только от объема выборки n. Доказательство этого факта основано на том, что статистика 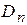 не изменяет своего значения при монотонных преобразованиях оси x. Таким преобразованием любое непрерывное распределение G(x) можно превратить в равномерное на отрезке [ 0,1 ]. При этом
не изменяет своего значения при монотонных преобразованиях оси x. Таким преобразованием любое непрерывное распределение G(x) можно превратить в равномерное на отрезке [ 0,1 ]. При этом 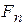 (x) перейдет в функцию распределения выборки из этого равномерного распределения.
(x) перейдет в функцию распределения выборки из этого равномерного распределения.
При малых n для статистики 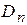 при гипотезе Н0 составлены таблицы процентных точек, например в [ 1 ] они доведены до n =100. При больших n распределение
при гипотезе Н0 составлены таблицы процентных точек, например в [ 1 ] они доведены до n =100. При больших n распределение 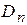 (при гипотезе Н0) указывает найденная в 1933 г. А.Н.Колмогоровым предельная теорема, которая утверждает, что при справедливости Н0 (и если G(x) непрерывна) вероятность
(при гипотезе Н0) указывает найденная в 1933 г. А.Н.Колмогоровым предельная теорема, которая утверждает, что при справедливости Н0 (и если G(x) непрерывна) вероятность 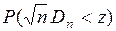 при неограниченном возрастании n имеет предел, и дает его выражение:
при неограниченном возрастании n имеет предел, и дает его выражение:
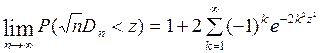
 ,
,
или
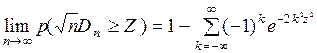 .
.
Для этих выражений имеются соответствующие таблицы, например, cм. [1]. Таким образом, задав значение вероятности ошибки первого рода a, можно определить величину порога, с которой будет сравниваться значение пороговой статистики 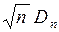 для вынесения решения об истинности гипотезы Н0. Статистика
для вынесения решения об истинности гипотезы Н0. Статистика 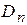 вычисляется по формуле
вычисляется по формуле
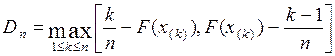 ,
,
где через x(1), x(2),... x(n) обозначены элементы вариационного ряда, построенного по исходной выборке, т.е., если элементы выборки расположить в порядке возрастания их значений, то x(i) обозначает элемент выборки, который стоит на i -м месте.
Критерий согласия омега-квадрат основан на статистике
 ,
,
которая измеряет расстояние между Fn(x) и F(x) в интегральной метрике.
Для вычисления 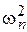 по реальной выборке можно использовать формулу:
по реальной выборке можно использовать формулу:
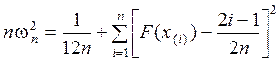 .
.
При справедливости гипотезы Н0: F(x)=G(x) и непрерывности функции G(x) закон распределения статистики 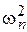 , так же как закон распределения статистики
, так же как закон распределения статистики 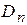 , зависит только от n и не зависит от G. Так же как для
, зависит только от n и не зависит от G. Так же как для 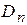 , для
, для 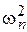 при малых значениях n имеются таблицы процентных точек, а для больших значений n следует использовать предельный (при n ®¥) закон распределения статистики n
при малых значениях n имеются таблицы процентных точек, а для больших значений n следует использовать предельный (при n ®¥) закон распределения статистики n 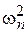 . Предельный закон распределения был найден Н.В.Смирновым в 1939 г. [ 1 ].
. Предельный закон распределения был найден Н.В.Смирновым в 1939 г. [ 1 ].
Следует отметить, что критерии, основанные на 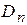 и
и 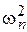 , состоятельны против любой альтернативы G(x)¹F(x). Статистический критерий для проверки гипотезы Н0 называется состоятельным против альтернативы Н1, если его мощность стремится к единице при неограниченном увеличении объема выборки.
, состоятельны против любой альтернативы G(x)¹F(x). Статистический критерий для проверки гипотезы Н0 называется состоятельным против альтернативы Н1, если его мощность стремится к единице при неограниченном увеличении объема выборки.
Рассмотренные критерии имеют ограниченную область применения, поскольку требуют непрерывности функции F(x). Например, они не применимы для дискретных законов распределения. Поэтому полезно познакомиться с более универсальным критерием К.Пирсона (1900 г.). Он основан на сравнении гипотетического (теоретического) закона распределения w(x) и гистограммы, построенной по выборке x.
Рис.
В качестве пороговой статистики, которая называется статистикой хи-квадрат Пирсона для простой гипотезы, используется величина 
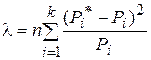 ,
,
(случайная величина l имеет распределение вероятностей  , поэтому в левой части последнего равенства пишут
, поэтому в левой части последнего равенства пишут  и критерий называют критерием хи-квадрат (
и критерий называют критерием хи-квадрат ( )), где Pi - вероятность (теоретическая, гипотетическая) того, что случайная величина попадет в интервал
)), где Pi - вероятность (теоретическая, гипотетическая) того, что случайная величина попадет в интервал 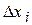 ;
;
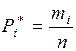 - оценка истинной вероятности (относительная частота);
- оценка истинной вероятности (относительная частота);
n - общее количество испытаний (размер выборки);
mi - количество испытаний, при которых значения случайных величин попали в интервал 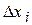 ;
;
k - количество интервалов на которое разделена область определения случайной величины.
На практике пороговую статистику удобнее вычислять по формуле
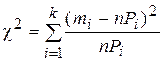 .
.
К.Пирсон доказал, что статистика  асимптотически подчиняется распределению
асимптотически подчиняется распределению  (хи-квадрат) с (k-1) степенями свободы.
(хи-квадрат) с (k-1) степенями свободы.
Рассмотренные правила проверки статистических гипотез позволяют принять или отвергнуть гипотезу Н0 при заданном уровне значимости a, но при этом теряется представление о мере расхождения (или степени согласованности) гипотетического закона распределения и гистограммы, построенной по конкретной (полученной) выборке x. В частности, такой мерой являются значения пороговых статистик X2 (критерий Пирсона) и  (критерий Колмогорова), но пользоваться ими из-за большого количества значений пороговых статистик и трудностей физической интерпретации не всегда удобно.
(критерий Колмогорова), но пользоваться ими из-за большого количества значений пороговых статистик и трудностей физической интерпретации не всегда удобно.
Рассмотрим более универсальную меру [ 2 ], инвариантную по отношению ко всем критериям, которые основаны на вычислении пороговой статистики. Все возможные выборки образуют пространство элементарных событий с общей вероятностной мерой, равной единице. Каждой выборке соответствует свое значение пороговой статистики ( или
или 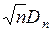 ), характеризующее степень согласованности (совпадения) теоретического и статистического законов распределения, причем чем больше значение пороговой статистики, тем меньше степень согласованности.
), характеризующее степень согласованности (совпадения) теоретического и статистического законов распределения, причем чем больше значение пороговой статистики, тем меньше степень согласованности.
Полученная (эмпирическая) выборка, которой соответствует некоторое значение пороговой статистики, например 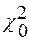 , является граничной между выборками, которым соответствует значение
, является граничной между выборками, которым соответствует значение  <
< 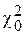 , и выборками, которым соответствуют значения
, и выборками, которым соответствуют значения 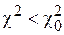 . Поэтому вероятностную меру P(
. Поэтому вероятностную меру P(  ) выборок, которые “хуже” полученной, можно использовать в качестве искомой меры согласованности законов распределения.
) выборок, которые “хуже” полученной, можно использовать в качестве искомой меры согласованности законов распределения.
При вычислении вероятности P(  ) необходимо учитывать зависимость закона распределения
) необходимо учитывать зависимость закона распределения  от параметра r, называемого числом степеней свободы распределения. Число степеней свободы равно числу интервалов k минус число независимых ограничений (связей) наложенных на частоты
от параметра r, называемого числом степеней свободы распределения. Число степеней свободы равно числу интервалов k минус число независимых ограничений (связей) наложенных на частоты 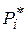 .
.
Примерами таких ограничений могут быть
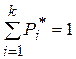 ,
,
если мы требуем только того, чтобы сумма частот была равна единице (это требование накладывается во всех случаях);
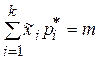 ,
,
если мы подбираем теоретическое распределение таким образом, чтобы его математическое ожидание m совпало со статистическим средним значением;
 ,
,
если мы требуем, кроме того, совпадения теоретической 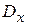 и статистической дисперсий. В данном случае статистическая оценка дисперсии является приближенной в силу того, что все значения, попавшие в интервал
и статистической дисперсий. В данном случае статистическая оценка дисперсии является приближенной в силу того, что все значения, попавшие в интервал 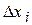 , заменяются на некоторое значение
, заменяются на некоторое значение 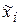 из этого интервала,
из этого интервала,  - выборочное среднее. Следует отметить, что ограничения на
- выборочное среднее. Следует отметить, что ограничения на 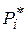 задаются только в виде линейных уравнений относительно переменных
задаются только в виде линейных уравнений относительно переменных 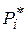 .
.
Пример. Пусть имеются результаты измерений (выборка размера n =500) сведенные в статистический ряд:
 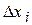
| -4; -3 | -3; -2 | -2; -1 | -1; 0 | 0; 1 | 1; 2 | 2; 3 | 3; 4 |
| mi | ||||||||
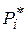
| 0,012 | 0,05 | 0,144 | 0,266 | 0,240 | 0,176 | 0,092 | 0,02 |
где 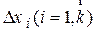 интервалы, на которые разбита область определения случайной величины; mi - количество реализаций (значений) случайной величины, попавших в интервал
интервалы, на которые разбита область определения случайной величины; mi - количество реализаций (значений) случайной величины, попавших в интервал 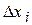 ;
;  - относительная частота попадания значений случайной величины в заданный интервал
- относительная частота попадания значений случайной величины в заданный интервал 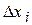 ; при этом
; при этом 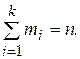 Графически статистический ряд оформляется в виде гистограммы.
Графически статистический ряд оформляется в виде гистограммы.
Проверим согласованность статистического распределения и теоретического (гипотетического), в качестве которого возьмем нормальный (гауссовский) закон распределения с параметрами, значения которых m = 0,168 и s = 1,448 совпадают с их статистическими оценками.
Зная теоретический закон распределения, можно найти теоретические вероятности попадания случайной величины в каждый из интервалов 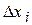 :
:
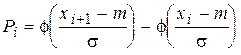 ,
,
где 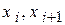 - границы i -го интервала,
- границы i -го интервала,
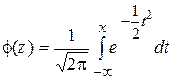
В таблице приведены значения функции 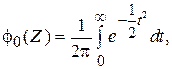
причем 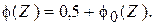
Пороговая статистика 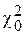
 в этом случае равна
в этом случае равна
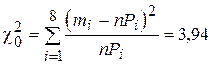 .
.
Если мы подбираем теоретическое распределение с тем условием, чтобы его математическое ожидание и дисперсия совпали с их статистическими оценками, то число степеней свободы r = 8-3 =5. По таблицам при r =5 находим, что
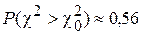 .
.
Если же на математическое ожидание и дисперсию не накладывать ограничений, а задать их значения априорно, то r = 8-1 = 7. Тогда при тех же значениях параметров (m =0,168, s=1,448), но заданных априорно, 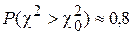 .
.
Задание и порядок выполнения работы
1. Составить программу для генератора случайных величин с произвольным заданным законом распределения (лабораторная работа №5). Задать конкретный вид закона распределения (т.е. выбрать вариант задания) и получить массив чисел (выборку) размера n.
2. Составить программу для вычисления пороговых статистик  и Z или
и Z или 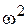
 по полученной выборке. Вычислить значения пороговых статистик для двух случаев:
по полученной выборке. Вычислить значения пороговых статистик для двух случаев:
а) когда гипотеза совпадает с истинным законом распределения;
б) когда гипотеза отличается от истинного закона распределения.
3. Объяснить различия в полученных результатах.
4. Исследовать зависимость результатов от размера выборки n.
5. Проверить истинность гипотезы. Для этого по заданному уровню значимости a с использованием таблиц определить пороги для критериев Пирсона и Колмогорова и сравнить с ними соответствующие пороговые статистики. Гипотезы проверить для случая а и б.
6. По таблицам определить вероятностную меру согласованности статистического и гипотетического законов распределения 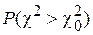 и
и  . Дать физическую интерпретацию полученных результатов.
. Дать физическую интерпретацию полученных результатов.
Указания к составлению отчета
Отчет должен содержать алгоритм, текст рабочей программы, результаты вычислений и физическую интерпретацию.
Вопросы для самопроверки
1. В чем различие между проверкой статистических гипотез и критериями согласия.
2. Как ведет себя пороговая статистика при неограниченном возрастании размера выборки n, когда гипотеза не совпадает с истинным законом распределения и когда совпадает.
3. В чем ограниченность критериев Колмогорова и 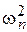 по сравнению с критерием Пирсона.
по сравнению с критерием Пирсона.
Рекомендуемая литература
1. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1983. - 416 с.
2. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1969. - 576 с.
Дата публикования: 2015-07-22; Прочитано: 351 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
