Свойства определителей

1. Если в определителе поменять местами какие-либо две строки (или столбца), то определитель изменит знак, не изменившись по абсолютной величине.

2. При умножении столбца (или строки) определителя на число определитель умножается на это число.

3. Если в определителе строки или столбцы одинаковы или пропорциональны, то определитель равен нулю.

4. Если определитель содержит нулевой столбец или нулевую строку, то он равен нулю.

5. Определитель не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.

6. Если для элементов какой- либо строки или столбца определителя верно соотношение: d = d₁ ± d₂, e = e₁ ± e₂, f = f₁ ± f₂, то верно:

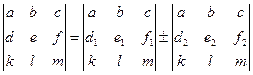
Матрицы.

Матрицей размера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются a_ij, где i- номер строки, а j- номер столбца.

А =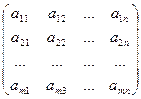

Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.

Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

Матрица вида:

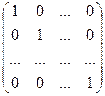= E,

называется единичной матрицей.

Квадратная матрица вида 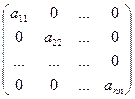называется диагональной матрицей.

Основные действия над матрицами.

Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:

Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

С = А ± В

c_ij = a_ij ± b_ij

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

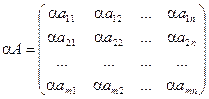
Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:

A×B = C;

.

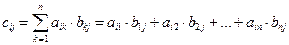Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

АВ ¹ ВА даже если определены оба произведения.

Если соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.

А×Е = Е×А = А

A×O = O; O×A = O, где О – нулевая матрица.

Матрицу В называют транспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.

А = 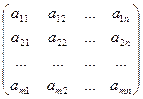; В = А^Т= ;

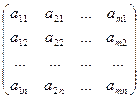т.е. b_ji = a_ij.

Элементарными преобразованиями матрицы называются следующие преобразования:

1) умножение строки (столбца) на число, отличное от нуля;

2) прибавление к одной строке (столбцу) другой строки;

3) перестановка строк(столбцов);

4) вычеркивание (удаление) одной из одинаковых строк (столбцов);

5) транспонирование;

Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.

Обратная матрица.

Определим операцию деления матриц как операцию, обратную умножению.

Если существуют квадратные матрицы Х и А, удовлетворяющие условию:

XA = AX = E,

где Е - единичная матрица того же самого порядка, то матрица Х называется обратной к матрице А и обозначается А^-1.

Каждая квадратная матрица с определителем DА, не равным нулю имеет обратную матрицу и притом только одну.

Определителем матрицы А называется определитель DА, состоящий из ее элементов.

Ранг матрицы.

Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.

В матрице порядка m´n минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n.

Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.

Порядок базисного минора матрицы называется рангом матрицы и обозначается r(A)=rg(A)=rang(A).

Элементарные преобразования матриц не изменяют ранг матрицы.

Матрица, на главной диагонали которой стоит подряд несколько единиц, а все остальные элементы равны нулю, называется канонической.

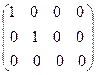
Число единиц канонической матрицы определяют ее ранг.

Т.е. для отыскания ранга матрицы достаточно привести ее к каноническому виду с помощью элементарных преобразований.

Следом (треком) квадратной матрицы 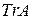называется сумма диагональных элементов

Методы решения систем линейных уравнений.

Матричный метод.

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Пусть дана система уравнений:

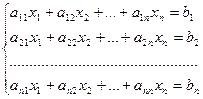
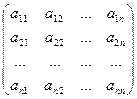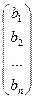Составим матрицы: A = ; B = ; X = .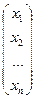

Систему уравнений можно записать:

A×X = B.

Сделаем следующее преобразование: A^-1×A×X = A^-1×B, т.к. А^-1×А = Е, то Е×Х = А^-1×В, тогда

Х = А^-1×В

Метод Крамера.

Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо, чтобы определитель матрицы системы не равнялся 0.

DA ¹ 0, тогда

Система из n уравнений с n неизвестными

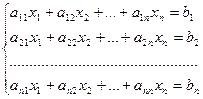
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

x_i = D_i/D,

где D = det A, а D_i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i.

D_i =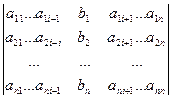

Если система однородна, т.е. b_i = 0, то при D¹0 система имеет единственное нулевое решение x₁ = x₂ = … = x_n = 0.

При D = 0 система имеет бесконечное множество решений.

Решение произвольных систем линейных уравнений.

Система m уравнений с n неизвестными в общем виде записывается следующим образом:

,

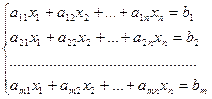где a_ij – коэффициенты, а b_i – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.

Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.

Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.

Для системы линейных уравнений (СЛУ) вида 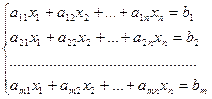матрица

А = 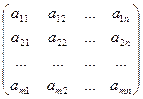называется матрицей системы, а матрица

А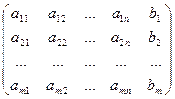^*= называется расширенной матрицей системы

Если b₁, b₂, …,b_m = 0, то система называется однородной, однородная система всегда совместна.

К элементарным преобразованиям СЛУ относятся:

1)Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю.

2)Перестановка уравнений местами.

3)Удаление из системы уравнений, являющихся тождествами для всех х.

Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

rg(A) = rg(A^*).

Метод Гаусса.

Суть метода заключается в последовательном исключении неизвестных.

Рассмотрим систему линейных уравнений:

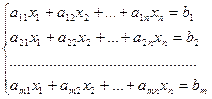
Разделим обе части 1–го уравнения на a₁₁ ¹ 0, затем:

1) умножим на а₂₁ и вычтем из второго уравнения

2) умножим на а₃₁ и вычтем из третьего уравнения

и т.д.

Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д. В итоге получим ступенчатую систему

,

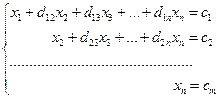Из последнего уравнения которой найдем x_n, подставим его в предпоследнее уравнение – найдем x_n-1, и т.д.

Если в процессе решения получается уравнение вида 0=с_k, тогда заданная система линейных уравнений несовместна.

Если получается уравнение вида 0=0, заданная СЛУ неопределенная. При этом решение системы находят, выразив главные неизвестные (стоящие на главной диагонали после удаления нулевого уравнения) через побочные (остальные).

Рассмотрим систему m линейных однородных уравнений с n – неизвестными

(*)

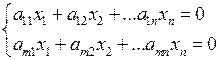Система линейно независимых решений 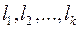называется фундаментальной, если каждое решение системы (*) можно представить в виде линейной комбинации .

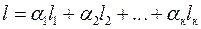Собственными числами квадратной матрицы 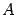являются корни характеристического уравнения 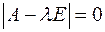и только они.

Собственным вектором матрицы А называется вектор 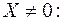если 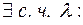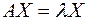, т.е. при умножении вектора Х на матрицу А он переходит в коллинеарный себе.

Чтобы найти собственный вектор, решаем уравнение 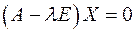для каждого собственного числа, находим фундаментальную систему его решений.

Нормой матрицы A называется вещественное число 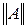, удовлетворяющее первым трём из следующих условий:

1. 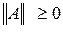, причём 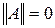только при ;

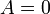2. 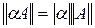, где ;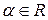

3. ;

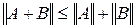4. .

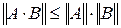Если выполняется также и четвёртое свойство, норма называется мультипликативной.

Существуют разные виды норм:

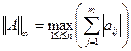
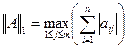
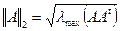
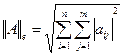-Евклидова

Числом обусловленности матрицы называются .