В равнобедренном прямоугольном треугольнике медиана, проведенная к гипотенузе равна 8 см. Найдите площадь этого треугольника

Задачи

1.Угол между стрелками часов в 9 часов превышает угол между стрелками часов в данный момент времени в 3 раза. Какое время показывают часы, если минутная стрелка показывает 12 часов?

2.Часы показывают 9 ч. Какое ближайшее время покажут часы, если угол между стрелками часов уменьшится в 3 раза?

3.Стороны одного угла перпендикулярны сторонам другого. Найдите каждый из этих углов, если один из них в четыре раза больше другого.

4. Стороны одного угла соответственно параллельны сторонам другого. Найдите каждый из этих углов, если один из них в четыре раза больше другого.

Таблица 2

Геометрический объект	Смежные углы	Внешний угол треугольника
Определение	Смежными углами называют углы, которые имеют одну общую сторону, а две другие их стороны дополняют друг друга до прямой	Угол, смежный с внутренним углом треугольника, называется внешним углом треугольника.
Изображение	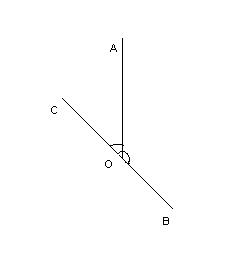Углы AOC и AOB – смежные	Угол BCD- внешний угол треугольника ABC.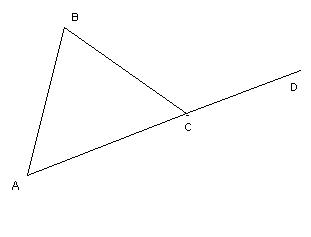
Свойства	1.Сумма смежных углов равна 180º. 2. Биссектрисы смежных углов перпендикулярны.	3.Внешний угол треугольника равен сумме внутренних, с ним не смежных.
Примечания		4.Внешний угол больше каждого внутреннего не смежного с ним.

Задачи

1.Внешний угол треугольника в два раза больше одного из внутренних, не смежных с ним углов. Найти все углы треугольника, если один из его внутренних углов равен 140º.

2.Угол между биссектрисой одного из смежных углов и стороной другого смежного угла равен 130º. Найдите эти

смежные углы.

Таблица 3

Геометрический объект	Вертикальные углы	Перпендикулярные прямые
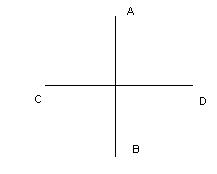
Определение	Вертикальными углами называются углы, стороны которых дополняют друг друга до прямых.	Если вертикальные углы, образованные пересекающимися прямыми, прямые (равны по 90º), то такие прямые называются перпендикулярными
Изображения	Углы BOC и AOD – вертикальные
Свойства	1.Вертикальные углы равны. 2. Биссектрисы вертикальных углов образуют развернутый угол.	3.Через данную точку к данной прямой можно провести только одну прямую, перпендикулярную данной. 4.Перпендикуляр, проведенный к отрезку в его середине, является геометрическим местом точек, равноудаленных от сторон угла.
Примечания

Задачи

1.Угол между биссектрисой одного из вертикальных углов и стороной другого вертикального угла равен 140º. Найдите эти вертикальные углы.

Таблица 4

	Треугольник	Виды треугольников
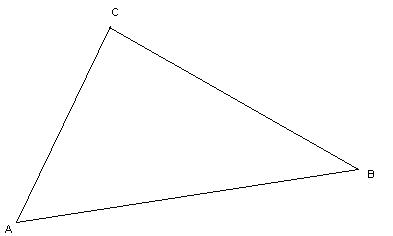
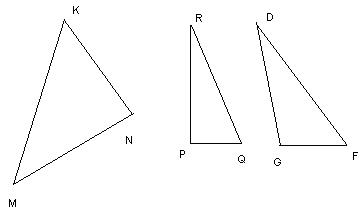
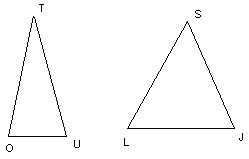
Определение	Треугольник- это геометрическая фигура, образованная тремя точками, не лежащими на одной прямой и тремя отрезками, соединяющими эти точки.   Точки (M,D,K) называются вершинами треугольника, а отрезки (MD,DK,KM) сторонами треугольника. Углы MDK, DMK, MKD называются углами треугольника.	·.Остроугольные: все углы острые (MKN), · Прямоугольные:один из углов треугольника прямой (RPQ). · Тупоугольные:один из углов треугольника тупой (DGF).   · Если две стороны треугольника равны, то треугольник называется равнобедренным. (OTU)Две равные стороны треугольника (OT, OU) называются боковыми, а третья сторона - основанием (TU).   · Если все стороны треугольника равны, то треугольник называется равносторонним (LSG).
Изображение	.	.
Свойства	1. Каждая сторона треугольника меньше суммы двух других его сторон. В ΔАВС АС+ ВС > AB AB +АС > BC BC+ AB > AC   2. Сумма угловлюбого треугольника равна 180˚.     3. Теорема синусов в произвольном треугольнике стороны пропорциональны синусам противолежащих углов, коэффициент пропорциональности равен диаметру описанной окружности.   4.Теорема косинусов Во всяком треугольнике квадрат любой его стороны равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними: 4a)Определение вида треугольника по длинам его сторон. Если в треугольнике квадрат наибольшей стороны равен сумме квадратов двух других сторон, то такой треугольник – прямоугольный, если меньше – то остроугольный, если больше – то тупоугольный.     5. Около любого треугольника можно описать окружность. Центр этой окружности – точка пересечения перпендикуляров, проведенных к сторонам треугольника в их серединах. 6. В любой треугольник можно вписать окружность. Центр этой окружности – точка пересечения биссектрис треугольника.	.   7. Углы при основании равнобедренного треугольника равны.   8. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой треугольника.   9.Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине этой гипотенузы и равна радиусу описанной около прямоугольника окружности. 10. Теорема Пифагора. 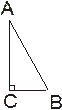В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы: a² + b² = c²   11.В прямоугольном треугольнике отношение катета, противолежащего острому углу, к гипотенузе равно синусу этого угла: 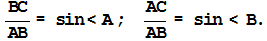12.В прямоугольном треугольнике отношение катета, прилежащего острому углу, к гипотенузе равно косинусу этого угла: 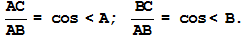    13.В прямоугольном треугольнике отношение катета, противолежащего острому углу, к прилежащему катету равно тангенсу этого угла: 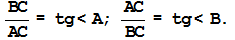  14.В прямоугольном треугольнике отношение катета, прилежащего острому углу, к противолежащему катету равно котангенсу этого угла 15. Высота, проведенная к гипотенузе, делит прямоугольный треугольник на два подобных треугольника (ACH и CHB). 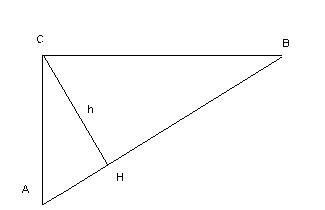16*. В прямоугольном треугольнике ABC обозначим h c – высоту, проведенную к гипотенузе, ac, b c - отрезки, на которые высота делит гипотенузу с, прилежащие соответственно к катетам a и b. 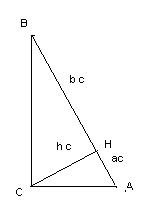Тогда справедливы формулы:   a) hc2 = ac b c; b) a2 = c ac; c) b2 = c b c ; d) a 2: b2 = b c: ac.   17*.В прямоугольном треугольнике r = p – c; r = (a + b – c)/2, r = p- 2R; r – радиус вписанной в треугольник окружности R – радиус описанной около треугольника окружности. 18*. Радиусы окружностей, вписанных в данный прямоугольный треугольник (rc) и треугольники, на которые высота, проведенная к гипотенузе, делит этот треугольник(ra, rb), связаны соотношением rc 2 = r a 2 + r b2 .
Примечания	7.Признаки равенства треугольников: 1.(По двум сторонам и углу, заключенному между ними). Если две стороны и угол, заключенный между ними одного треугольника соответственно равны двум сторонам и углу, заключенному между ними другого треугольника, то такие треугольники равны. 2.(По стороне и двум прилежащим к ней углам). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. 3. (По трем сторонам). Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. 4*. Если две стороны и угол, прилежащий к одной из сторон одного треугольника, соответственно равны двум сторонам и углу, прилежащему к соответствующей стороне другого треугольника, то эти треугольники равны, если они оба тупоугольные, либо остроугольные, в противном случае сумма двух их углов равна 180º.	19.В правильном треугольнике со стороной a высота h выражается через эту сторону: h = a 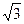/2 20.В прямоугольном треугольнике катет, лежащий против угла в 30º, равен половине гипотенузы. 21**. В равнобедренном треугольнике сумма расстояний от любой точки основания до боковых сторон равнобедренного треугольника есть величина постоянная для данного треугольника.

Задачи

1.В прямоугольном треугольнике 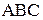из вершины прямого угла B проведена высота BP. Найдите косинус угла А, если выполнено условие .

2. В равнобедренном треугольнике боковая сторона в 1,5 раза больше радиуса описанной около треугольника окружности. Найдите угол, который образует боковая сторона с основанием.

Ответ: arcsin3/4.

3.

В треугольнике ABC прямая, соединяющая вершину B c центром описанной около треугольника окружности O, пересекает сторону AC в точке K. Известно, что AK:KC = 4:1, sin<ABC= 0,75. Найдите отношение OK:OB.

= 8/15 AC. OK:OB = 8/15 AC: AC/3 = 4:5.

Ответ: 4:5.

4. На стороне основания равнобедренного треугольника взята точка M, сумма расстояний от которой до сторон угла равно 10 см. Найдите высоту треугольника, проведенную к боковой стороне.

4.21 MK+MN = 2 OL. Отрезок OL – средняя линия треугольника AHB, поэтому AH = 2 OL = 10см.

Ответ: 10см.

5. Определить периметр равнобедренного треугольника, если его основание равно 5, а радиус вписанной окружности

равен 1.

Таблица 5

Геометрический объект	Биссектриса треугольника	Биссектриса угла
Определение	Биссектриса треугольника – это отрезок биссектрисы угла треугольника от вершины треугольника до противоположной стороны	Биссектриса угла – это луч, выходящий из вершины угла и делящий его на два равных угла.
Изображение		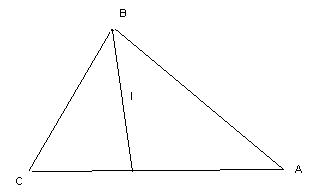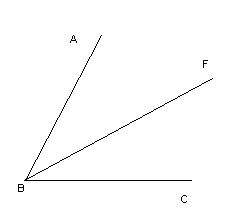Луч BF- биссектриса угла ABC,
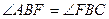
Свойства	1.Три биссектрисы треугольника пересекаются в одной точке. 2.Биссектриса угла треугольника делит сторону, противоположную этому углу, на части, пропорциональные прилежащим сторонам.   3*.Длину биссектрисы можно вычислить по формуле: la= 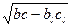, где la - длина биссектрисы, проведенной из угла A треугольника ABC, bl, al - отрезки, на которые биссектриса делит сторону BC, b, a - длины сторон треугольника.   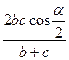4*.Длину биссектрисы можно вычислить по формуле: la= , где la - длина биссектрисы, проведенной из угла A треугольника ABC, α = 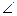BAC, b, a - длины сторон треугольника. 5.*Тупой угол между биссектрисами, двух углов треугольника равен α/2 + 90º, где α – величина третьего угла треугольника.   6*. Площадь треугольника, вершинами которого являются основания биссектрис, равна , где S – площадь данного треугольника, a,b,c – его стороны. 7*.Биссектриса внешнего угла треугольника пересекает противоположную сторону в точке, отношение расстояний от которой до концов этой стороны равно отношению двух других сторон треугольника.	.   8. Биссектриса угла является геометрическим местом точек, равноудаленных от сторон угла.
Примечания

Задачи

1.Длины катетов прямоугольного треугольника равны 3 см и 6 см. Найдите длину биссектрисы, проведенной из вершины прямого угла.

2.В прямоугольный треугольник с катетами 8 см и 12 см вписан полукруг с диаметром, лежащем на гипотенузе. Найдите радиус этого полукруга.

3.Длина основания равнобедренного треугольника равна 2, а длина боковой стороны 3. К одной из боковых сторон проведена высота, а к другой – биссектриса. Найдите отношение длин отрезков, на которые биссектриса делит высоту.

4. Зная длины сторон AB=3, BC= 6, AC= 3 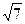треугольника ABC, найдите величину угла AOC, где O- центр

окружности, вписанной в треугольник ABC.

5.В треугольнике ABC угол B равен 45º. Из основания K биссектрисы CK проведены перпендикуляры KM и KN к сторонам AB и AC соответственно. Найдите отношение длин сторон AB и AC, если CN = MN.

Решение

Таблица 6

Геометрический объект	Высота треугольника	Ортоцентрический треугольник
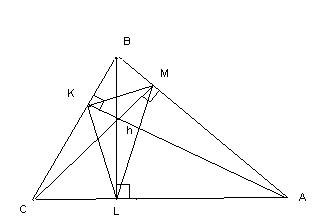
Определение	Высота треугольника– это отрезок перпендикуляра от вершины до противоположной стороны.	Треугольник, вершины которого есть основания высот данного, называется ортоцентрическим.
Изображение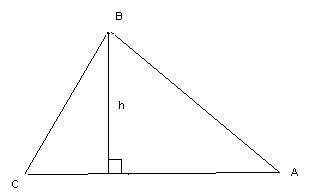
Свойства	1.Прямые, содержащие высоты треугольника пересекаются в одной точке (в ортоцентре треугольника). 2*. Отрезок, соединяющий основания высот остроугольного треугольника, отсекает от данного треугольника, подобный ему с коэффициентом подобия, равным косинусу общего угла этих треугольников. 3. Из двух высот треугольника большая высота проведена к его меньшей стороне. 4*. Разность квадратов двух сторон треугольника равна разности квадратов отрезков, на которые высота, проведенная к третьей стороне треугольник, делит эту сторону.	5**. Высоты данного остроугольного треугольника являются биссектрисами углов ортоцентрического. 6**.Площадь ортоцентрического треугольника S1 выражается через площадь S данного по формуле:   S1 = 2ScosA cosB cosC.   7**. Радиусы описанной около данного треугольника окружности, проведенные в вершины треугольника, перпендикулярны сторонам ортоцентрического треугольника 8**. Углы ортоцентрического треугольника равны 180º- 2α, 180º- 2β, 180º- 2γ, где α,β,γ – углы данного треугольника.
Примечания

Задачи

1.Стороны треугольника равны 16, 17, 18 см. найдите высоту, проведенную к средней стороне.

2. Отрезок, соединяющий основания двух высот остроугольного треугольника, равен 5см. Найдите сторону треугольника, противолежащую этому отрезку, если угол, противолежащий этой стороне равен 30°.

3. Отрезок, соединяющий основания двух высот остроугольного треугольника, равен 4см. Сторона треугольника, противолежащая этому отрезку равна 5см. Найдите радиус окружности, описанной около данного треугольника.

4. Окружность проходит через основания всех высот тупоугольного треугольника. Найдите ее радиус, если наибольшая сторона треугольника равна 4, а расстояние между основаниями высот, лежащими на продолжениях сторон треугольника, равно 3.

.

5. Стороны ортоцентрического треугольника равны 8, 15 и 17 см. Найдите радиус окружности, описанной около данного треугольника.

Таблица 7

Геометрический объект	Медиана треугольника	Средняя линия треугольника
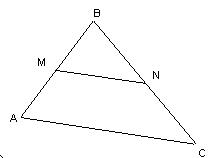
Определение	Отрезокот вершины треугольника до середины противоположной стороны	Отрезок соединяющий середины двух сторон треугольника называется средней линией треугольника.
Изображение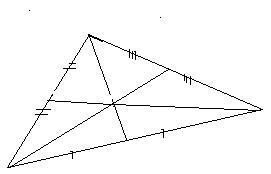
Свойства	1.Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2 к 1, считая от вершины. 2. Из двух медиан треугольника большая медиана проведена к его меньшей стороне. 3*. Длину медианы треугольника, можно вычислить по формуле: 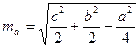  , где ma – длина медианы, проведенной к стороне a.	8.Средняя линия треугольника отсекает от него треугольник, подобный данному, площадь которого составляет 1/4 площади данного треугольника. 9.Треугольник, сторонами которого являются средние линии, подобен данному с коэффициентом подобия, равным ½. Площадь его составляет 1/4 площади данного треугольника.
Примечания	4*.Сумма квадратов медиан треугольника равна ¾ суммы квадратов его сторон. 5**.Сумма квадратов медиан прямоугольного треугольника равна 3/2 квадрата его гипотенузы. 6**.Сумма квадратов медиан прямоугольного треугольника, проведенных из вершин острых углов, равна 5/4 квадрата его гипотенузы. 7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна половине этой гипотенузы.

Задачи

1.Длины двух сторон треугольника равны 16 и 12 см. Медианы, проведенные к этим сторонам треугольника перпендикулярны. Найдите третью сторону треугольника.

Решение.

2. В параллелограмме ABCD угол BAD равен 60º. Точка K – середина стороны CD. Отрезки AK и BD пересекаются в точке E. Найдите длину стороны AB, если расстояние от точки E до прямой BC равно 2√3.

Таблица 8

Геометрический объект	Подобные треугольники	Пропорциональные отрезки
Определение	Два треугольника называются подобными, если их соответственные углы равны, а стороны, лежащие против этих углов, пропорциональны	Отрезки называются пропорциональными, если отношения их длин равны.
Изображение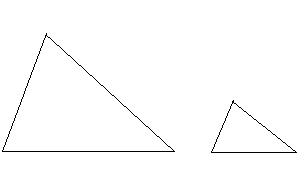
Свойства	1.Первый признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.   2.Второй признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между ними равны, то такие треугольники подобны. 3.Третий признак подобия треугольников. Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. 4.Отношение площадей подобных треугольников равно квадрату коэффициента подобия.	6. Теорема Фалеса Параллельные прямые отсекают на сторонах угла пропорциональные отрезки. 7*.Теорема Чевы Пусть точки A1, B1, C1 расположены на сторонах AB, BC, CA треугольника ABC или на их продолжениях. Для того, чтобы прямые AA1, BB1, CC1 пересеклись в одной точке или были параллельны, необход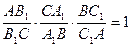имо и достаточно, чтобы .   8*.Теорема Менелая Пусть точки A1, B1, C1 расположены на сторонах AB, BC, CA треугольника ABC или на их продолжениях соответственно. Для того, чтобы точки A1, B1, C1 лежали на одной прямой, необходимо и достаточно, чтобы .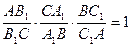
Примечания	5.Отношение площадей подобных фигур равно квадрату коэффициента подобия.	9. Отрезок, параллельный одной из сторон треугольника, отсекает от него треугольник, подобный данному. 10. Отношение периметров подобных треугольников равно отношению соответствующих сторон этих треугольников.

Задачи

1. В треугольнике ABC точки M и N делят стороны AB и BC в отношении 2:1, считая от вершины B.Найдите отношение площадей треугольников ABC и MBN.

3.Точки A₁, B₁, C₁ лежат на прямых AB, BC, CA соответственно, при этом, Найдите отношение BC₁ :C₁A, если эти точки лежат на одной прямой.

4. На сторонах AB и AC треугольника ABC даны соответственно точки M и N такие, что 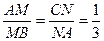, точка K делит отрезок CB внешним образом, в отношении BK: CK = m: n. Найдите отношение m: n, если точки M, N, K лежат на одной прямой,

5. В параллелограмме ABCD угол BAD равен 60º. Точка K – середина стороны CD. Отрезки AK и BD пересекаются в точке E. Найдите длину стороны AB, если расстояние от точки E до прямой BC равно 2√3.

6. В треугольнике ABC точки E и K делят сторону AC на три равные части, причем, E лежит между точками A и K.

На стороне BC взята точка D так, что отрезок AD пересекает BE в точке N и отрезок BK в точке M, причем AN:NM = 11:3. Найдите BD:DC.

7. Высота трапеции ABCD равна 7, а длины оснований AD и BC равны соответственно 8 и 6. Через точку E, лежащую на стороне CD, проведена прямая BE, которая делит диагональ AC в тоске O в отношении AO:OC = 3:2. Найдите площадь треугольника OEC.

8. В прямоугольном треугольнике высота треугольника делит его на два треугольника с площадями 4 и 9 см. Найдите катеты этого треугольника, если гипотенуза этого треугольника равна √13см.

Таблица 9

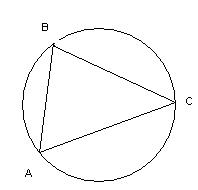
Геометрический объект	Окружность, вписанная в треугольник	Окружность, описанная около треугольника
Определение	Если стороны треугольника касаются окружности, то эта окружность вписана в треугольник, а треугольник описан около окружности.	Если вершины треугольника лежат на окружности, то эта окружность описана около треугольника, а треугольник вписан в окружность
Изображение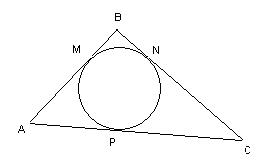
Свойства	1*. a)Отрезок стороны треугольника ABC от вершины A до точки касания вписанной окружности со стороной AC равен p- a, где p – полупериметр треугольника ABC, a – сторона треугольника. АК = p-a. b) Отрезок стороны AC треугольника ABC от вершины A до точки касания вневписанной окружности равен p- с, где p – полупериметр треугольника ABC, с – сторона треугольника. АК = p-с. 2.* Периметр треугольника, отсекаемого от данного касательной к вписанной в треугольник окружности, равен удвоенному отрезку стороны от вершины треугольника до точки касания, PAMN = 2AK. 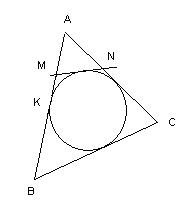  3*. Сумма обратных величин высот треугольника равна обратной величине радиуса вписанного круга: 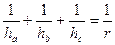  4**.Площадь треугольника, вершинами которого служат точки касания вписанного круга, равна 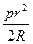. 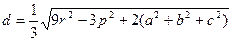5**.Расстояние от центра вписанной в треугольник окружности до точки пересечения медиан треугольника равно	6**.Расстояние от центра описанной окружности до ортоцентра равно 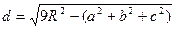7.**Расстояниемежду центрами вписанной и описанной окружности равно d = 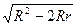8**.Во всяком треугольнике сумма расстояний от центра описанного круга до сторон треугольника равна сумме радиусов вписанного и описанного кругов (теорема Карно).
Примечания		9.Если треугольник остроугольный, то центр описанной около него окружности лежит внутри треугольника, если – прямоугольный- то на стороне (совпадает с серединой гипотенузы), если тупоугольный – то вне треугольника.

Задачи

1. Радиус описанной около равнобедренного треугольника с углом 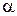при основании окружности равен 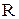. Найдите радиус окружности, вписанной в этот треугольник.

2.Угол при вершине равнобедренного треугольника равен 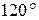. Найдите отношение площади круга, описанного около этого треугольника, к площади вписанного в него круга.

ABCD – ромб с острым углом BAD. Расстояние между центрами окружностей, описанных около треугольников ABD и BCD, равно √3, а между центрами окружностей, описанных около треугольников ABC и ACD, равно √6. Найдите радиус окружности, вписанной в ромб.

4.В прямоугольнике ABCD радиусы окружностей, вписанных в треугольники ABC и ACD, равны 2. Расстояние между точками касания этих окружностей с диагональю AC равно 7. Найдите стороны прямоугольника.

5.Из точки C к окружности проведены две касательные. На меньшей из дуг между точками касания выбрана произвольная точка. Касательная, проведенная в этой точке к окружности пересекает касательные, проведенные из точки C, образуя треугольник периметра 8см. Найдите длины отрезков касательных от точки C до точек касания с окружностью.

6.Внутри треугольника ABC взята произвольная точка O и через нее проведены прямые, параллельные сторонам треугольника. Эти прямые делят треугольник на шесть частей, три из которых являются треугольниками. Радиусы окружностей, вписанных в эти треугольники равны 3, 6 и 8см. Найдите радиус окружности, вписанной в треугольник ABC.

7.В треугольнике ABC, биссектрисы углов при вершинах A и C пересекаются в точке D. Найдите радиус окружности, описанной около треугольника ABC, если радиус окружности с центром в точке О, описанной около треугольника

8. Трапеция с основаниями a и b вписана в окружность, диагонали трапеции перпендикулярны. Найдите радиус окружности.

9. Четырехугольник ABCD вписан в окружность радиуса 3 см. Сторона АD является диаметром окружности, СD= 4 см. Стороны АВ и ВС равны. Найдите эти стороны.

Решение

10.Периметр треугольника ABC равен p. К окружности, вписанной в треугольник

11. Точка К – точка касания окружности, касающейся стороны АС треугольника АВС и продолжений сторон АВ и ВС треугольника, со стороной АС. Найдите длину отрезка KM, где M – точка касания вписанной в треугольник АВС окружности со стороной АС, если АВ=7см, ВС=5см.

12. На основании AC равнобедренного треугольника ABC расположена точка D, так, что AD =6, DC = 8см. Окружности, вписанные в треугольники ABD и DBC, касаются прямой BD в точках M и N соответственно. Найдите длину отрезка MN.

Таблица 10

Математический объект	Параллелограмм	Параллельные прямые
Определение	Параллелограмм– это четырехугольник, у которого противоположные стороны попарно параллельны	Прямые, которые лежат в одной плоскости и не имеют общих точек, называются параллельными.
Изображение	.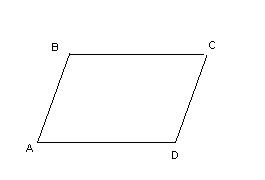
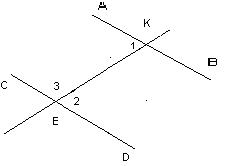
Свойства	1. Противоположные углы параллелограмма равны. 2. Противоположные стороны параллелограмма равны. 3. Диагонали параллелограмма точкой пересечения делятся пополам. 4. Каждая диагональ параллелограмма делит его на два равных треугольника. 5. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º. 6*.Сумма квадратов сторон параллелограмма равна сумме квадратов его диагоналей. 7.Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. 8. Биссектрисы углов параллелограмма при пересеченииобразуют прямоугольник, диагонали которого параллельны сторонампараллелограмма и равны разности соседних сторон параллелограмма. 9.* Угол между высотами параллелограмма равен острому углу параллелограмма.	11.Признакипараллельности прямых. 1. Если при пересечении двух прямых (AB и CD) третьей (KE) накрест лежащие углы равны (<1=<2), то эти прямые параллельны (рис.2). 2.Если при пересечении двух прямых (AB и CD) третьей (KE) сумма односторонних углов (<2 +<3 =180)º равна 180º, то эти прямые параллельны (рис2). 3.Если две прямые (a и b) перпендикулярны третьей (с), то эти прямые параллельны.
Примечания	10. Признаки параллелограмма 1.Если в четырехугольнике диагонали точкой пересечения делятся пополам, то такой четырехугольник – параллелограмм. 2.Если в четырехугольнике противоположные стороны попарно равны, то такой четырехугольник – параллелограмм. 3.Если в четырехугольнике две противоположные стороны равны и параллельны, то такой четырехугольник – параллелограмм.

Задачи

1.Сумма длин диагоналей параллелограмма равна 20см. Найдите периметр четырехугольника, вершины которого совпадают с серединами сторон данного параллелограмма

2.В параллелограмме ABCD угол A равен 76°, BM= 5см и MC=3см,<CMA = 142°, точка M лежит на стороне BC.

Найдите периметр параллелограмма ABCD.

3.Биссектриса большего угла параллелограмма отсекает от него равнобедренную трапецию с боковой стороной 4см. Найдите стороны параллелограмма, если меньшее основание трапеции равно 5см.

4.АВСD – параллелограмм, АВ =12 см, АС =16 см. Вершина D удалена от диагонали АС на 4 см. Вычислите расстояние от точки D до прямой АВ.

5.Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K и продолжение стороны CD в точке M. CM=1, BK=3. Найдите стороны параллелограмма.

Решение

6. Докажите, что биссектрисы углов параллелограмма при пересеченииобразуют прямоугольник, диагонали которого параллельны сторонампараллелограмма и равны разности соседних сторон параллелограмма.

7. Из вершины А параллелограмма АВСD c прямым углом САD опущен перпендикуляр АК на сторону СD. Известно, что АD=2АК=12. Из точки М, лежащей на отрезке КС, опущены перпендикуляры МР и МQ на стороны AD и АВ соответственно. В четырёхугольник MPAQ вписана окружность. Найдите её радиус.

8.В параллелограмме площади 4√2 см² отношение сторон равно отношению диагоналй; меньшая из диагоналей перпендикулярна одной из сторон параллелограмма. Найдите его стороны.

Решение

9. В параллелограмме с острым углом расстояния от точки пересечения диагоналей до неравных сторон параллелограмма равны 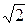см и 3 см. Найдите площадь параллелограмма.

Таблица11

Математический объект	Ромб	Высота ромба
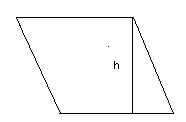
Определение	Ромб – это параллелограмм, у которого все стороны равны	Отрезок перпендикуляра, заключенный между параллельными сторонами, проведенный к одной из них.
Изображение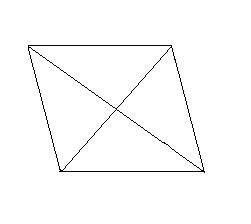
Свойства	1. Диагонали ромба перпендикулярны. 2. Диагонали ромба делят его углы пополам. 3. Высота ромба равна удвоенному радиусу вписанной окружности. 4. Если острый угол ромба равен 60º, то меньшая диагональ ромба равна его стороне.	5.Высоты ромба равны
Примечания	7*. Середины сторон ромба являются вершинами прямоугольника.	6.Расстояние от точки пересечения диагоналей ромба до его стороны равно половине высоты.

Задачи

1.Острый угол ромба равен 60°. Определите сторону ромба, если его меньшая диагональ равна 7см.

2. Отношение углов, которые диагонали ромба образуют с его стороной равно 1:2.

Найдите сторону ромба, если его меньшая диагональ равна 14см.

3. Середины сторон ромба являются вершинами некоторого четырехугольника. Найдите диагонали этого четырехугольника, если высота ромба равна 6см, а его острый угол равен 30°.

4.Вершины ромба лежат на различных сторонах прямоугольника. Если площадь прямоугольника равна 20 см², то какова площадь ромба?

5. Периметр ромба равен 48 см, а сумма длин его диагоналей равна 26см. Найдите его площадь.

Решение

Таблица 12

Геометрический объект	Прямоугольник
Определение	Прямоугольник – это параллелограмм, у которого все углы прямые.
Изображение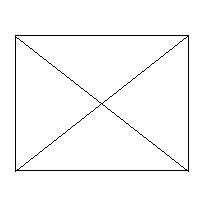
Свойства	1.В прямоугольнике диагонали равны. 2.Радиус описанной окружности около прямоугольника равен половине диагонали, а центр этой окружности совпадает с точкой пересечения диагоналей. 3**. Суммы квадратов расстояний от некоторой точки плоскости прямоугольника до двух его противоположных вершин равны. 4. Если угол между диагоналями прямоугольника равен 60º, то меньшая сторона прямоугольника равна половине диагонали прямоугольника.
Примечания	5*.Отрезки от вершины прямоугольника до середины противолежащей стороны делят пересекающую их во внутренних точках диагональ прямоугольника на три равные части.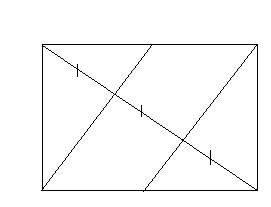

Задачи

1.В прямоугольнике ABCD проведены биссектрисы A K и CM углов A и C. Найдите KM:AB:AD (K 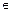BC, M 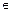AD), если AD вдвое больше AB.

2. Биссектрисы углов параллелограмма при пересечении образуют четырехугольник. Найдите длины его диагоналей, если длины сторон параллелограмма равны 2см и 6см.

3.Расстояния от некоторой точки плоскости прямоугольника до трех последовательных вершин прямоугольника равны 3, 4 и 5. Найдите расстояние от этой точки до четвертой вершины прямоугольника.

4.В прямоугольнике АВС D AB=a, BC=b. На стороне АВ как на диаметре построена окружность и к ней из вершины С проведена касательная, пересекающая строну АD в точке K. Найдите радиус окружности, вписанной в треугольник

С DK.

5. АВСD взята точка М так, что МВ= а, МС= b и МD =c. Найдите МА.

Таблица 13

Геометрический объект	Квадрат	Площадь квадрата
Определение	Квадрат – это ромб, у которого все углы прямые (или прямоугольник, у которого все стороны равны).
Изображение
Свойства	1.Диагональ (d) квадрата выражается через его сторону (a) в виде d = a 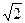. 2. Диагональ квадрата является диаметром окружности, описанной около квадрата. 3. Сторона квадрата является диаметром окружности, вписанной в квадрат.
Примечания

Задачи

1.В квадрате ABCD точка O - точка пересечения диагоналей. OK – биссектриса треугольника ABO. Найдите сторону квадрата, если OK = 10см.

2.Найдите площадь квадрата, вписанного в прямоугольный треугольник с катетами a и b (сторона квадрата лежит на гипотенузе, а две вершины – на катетах треугольника).

3. Сторона квадрата ABCD равна 1.Точки A и B лежат на окружности, а точки D и C вне окружности, длина отрезка касательной к которой, проведенной из точки C к этой окружности равна 2. Найдите диаметр окружности.

4.Дан квадрат со стороной a. Найдите площадь правильного треугольника, одна из вершин – середина стороны квадрата, а две другие лежат на диагоналях квадрата.

Решение.

Треугольник KML- правильный, при этом KL//AB. Применим к треугольнику AMK теорему синусов, получим AM/sin75°=MK/sin45°, откуда MK= a/2sin45/sin 75°, MK =a(√3-1)/2.

(sin75°=sin(45°+30°). Другой случай положения точек на диагоналях:K ₁L₁, Тогда рассматривается правильный треугольник M K ₁L₁,. Аналогично первому случаю, применяя теорему синусов к треугольнику MBK₁ , получим MK₁ = a(√3+1)/2.

Ответ: a(√3+1)/2.

5.Внутри квадрата ABCD выбрана точка M так, что углы MDC и MCD равны по 15°. Найдите угол AMB.

6. На сторонах квадрата ABCD AB и DC выбраны точки Е и F соответственно так, что AE:EB=CF: FD = 1:2. Отрезки AF и DE пересекаются в точке М, а CE и BF – в точке N.

Таблица 14

Геометрический объект	Трапеция	Средняя линия трапеции
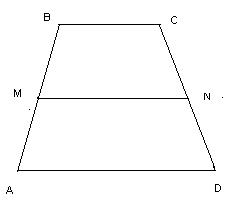
Определение	Трапеция– это четырехугольник, у которого две стороны параллельны, а две другие не параллельны. Параллельные стороны трапеции (AD и BC) называются основаниями трапеции, а не параллельные – боковыми сторонами (AB и CD).   Трапеция называется равнобокой, если боковые стороны ее равны.	Средней линией трапеции называется отрезок, который соединяет середины её боковых сторон отрезок MN на рис.8 - это средняя линия трапеции).
Изображение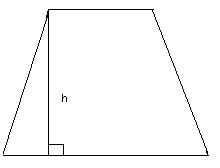
Свойства	1. В трапеции отношение ее оснований равно отношению отрезков диагоналей, на которые они делятся точкой пересечения.   2*.В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения прямых, на которых лежат боковые стороны, лежат на одной прямой. 3.В равнобокой трапеции углы при основании равны. 4. В равнобокой трапеции диагонали равны. 5*. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и проходит через точку пересечения диагоналей.   6*. В равнобокой трапеции больший из отрезков, на которые высота трапеции, проведенная из вершины, делит большее основание трапеции равен средней линией трапеции. 7*. Угол, под которым из центра вписанной в трапецию окружности видна ее боковая сторона, равен 90º.	8.Средняя линия трапеции параллельна основаниям и равна полусумме её оснований: MN=(AD + BC):2.   9.*8 Длина отрезка, параллельного основаниям трапеции, проходящего через точку пересечения диагоналей трапеции, заключенного между боковыми сторонами, равна среднему гармоническому оснований трапеции, т.е. 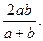10.**Отрезок, параллельный основаниям трапеции, который делит трапецию на две равновеликих, равен среднему квадратичному оснований трапеции.   11**. Отрезок, параллельный основаниям трапеции, который делит трапецию на две подобных, равен среднему геометрическому оснований трапеции.
Примечания

Задачи

1.Угол между прямыми, содержащими боковые стороны трапеции, равен 90°. Найдите

отрезок, соединяющий середины оснований трапеции, если основания трапеции равны 20 и 12см.

2. Угол между прямыми, содержащими боковые стороны трапеции, равен 90°. Найдите

отрезок, соединяющий середины оснований трапеции, если меньшая боковая сторона равна 4см, а меньший угол трапеции равен 30°.

3. Один из углов равнобедренной трапеции равен 60°. Боковая сторона трапеции равна 8 см. Найдите основания трапеции, если их сумма равна 12см.

4.Один из углов прямоугольной трапеции равен 60°, большая боковая сторона равна меньшему основанию. Найдите большую диагональ трапеции, если высота трапеции равна 4см.

5. В прямоугольной трапеции меньшая диагональ является биссектрисой тупого угла трапеции. Найдите большее основание, если ее большая боковая сторона равна 3 см.

6. В равнобедренной трапеции больший из двух отрезков, на которые высота делит большее основание равен 7см. Найдите длину отрезка, соединяющего середины боковых сторон трапеции

Решение

7.Продолжения боковых сторон трапеции пересекаются под прямым углом. Найти длину отрезка, соединяющего середины оснований, если боковые стороны равны 3 см и 4 см.

Решение

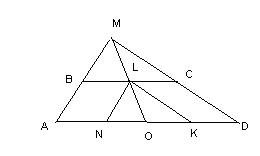
8. Продолжения боковых сторон трапеции пересекаются под прямым углом. Найти длину отрезка, соединяющего середины оснований, если основания трапеции равны 4 и 10 см.

9Основания трапеции равны 24 и 48.Определите длину отрезка, параллельного основаниям трапеции, проходящего через точку пересечения диагоналей трапеции, заключенного между ее боковыми сторонами.

10.В трапеции ABCD известны основания AD=7, BC=3. Прямая, параллельная основаниям трапеции, пересекает боковые стороны AB и СD в точках K и M. AK:KB=7:3. Найдите KM.

Таблица 15

Геометрический объект	Окружность, взаимное расположение окружностей.	Хорда, диаметр, касательная
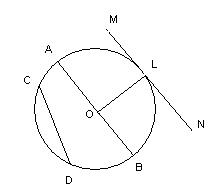
Определение	Окружность - это множество точек плоскости, расстояние от каждой из которых до данной точки (центра окружности) равно одному и тому же числу (радиусу окружности). .	Хордами окружности называются отрезки, соединяющие любые две точки окружности.CD– хорда окружности. Диаметром окружности называется хорда, проходящая через её центр. (AB –диаметр). Касательная к окружности – это прямая (MN), которая имеет с окружностью. только одну общую точку (L).
Изображение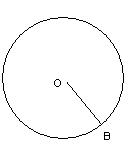
Свойства	1.Длина окружности вычисляется по формуле C = 2π R, π ≈ 3.14, R- радиус окружности. 2. Площадь круга вычисляется по формуле S = π R². 3. Две окружности касаются друг друга внешним образом тогда и только тогда, когда расстояние между их центрами равно сумме радиусов этих окружностей. 4.Две окружности касаются друг друга внутренним образом тогда и только тогда, когда расстояние между их центрами равно разности радиусов этих окружностей. 5.Если расстояние между центрами окружностей меньше суммы их радиусов, но больше разности то окружности пересекаются. 6*. Длина общей внешней касательной двух касающихся окружностей равна 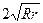, где r и R – радиусы этих окружностей. 7*. Если угол между внешними касательными к двум касающимся окружностям равен 60º, то отношение их радиусов равно 3. Справедливо и обратное: если отношение двух внешне касающихся окружностей равно 3, то угол между внешними касательными равен 60º 8*.Угол между хордами внешне касающихся окружностей проведенными из их точки касания в точки касания с их внешней касательной – прямой.	9.Касательная к окружности перпендикулярна радиусу (OL), проведенному в точку касания. 10.Если из точки к окружности проведены две касательные, то: а) отрезки касательных от этой точки до точек касания равны, б) прямая, проходящая через центр окружности и заданную точку, делит угол между касательными прямыми пополам. 11.Радиус, перпендикулярный хорде проходит через ее середину. 12.Дуги окружности, заключенные между параллельными хордами равны. 13. Равные дуги окружности стягиваются равными хордами. 14*. Если из точки М к окружности проведены касательная и секущая, то квадрат отрезка касательной от точки М до точки касания равен произведению длин отрезков секущей от точки М до точек ее пересечения с окружностью. 15*. Если из одной точки к окружности проведены две секущие, то произведения секущих на их соответствующие внешние части равны.
Примечания		Диаметр – наибольшая хорда окружности.

Задачи

1. Две окружности радиусов 4см и 1см касаются внешним образом. Найдите расстояние от точки касания окружностей до середины их обшей внешней касательной.

2. Три окружности попарно касаются друг друга внешним образом. Найдите площадь

треугольника с вершинами в центрах окружностей, если радиусы окружностей равны 8, 12, 16см.

3. Две окружности радиусов 6 и 2 см касаются внешним образом. Найдите угол между их внешними общими касательными.

Таблица16

Геометрический объект	Вписанный угол	Центральный угол, дуга, сектор.
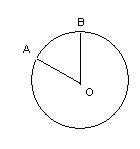
Определение	Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность	Центральным углом называется угол, вершина которого находится в центе окружности. Дугой окружности называется часть окружности, заключённая между двумя её точками Сектором круга называется часть круга, ограниченная двумя радиусами и дугой.
Изображение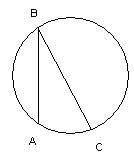
Свойства	1. Величина вписанного угла равна половине угловой величины дуги, на которую он опирается. 2.Вписанные в окружность углы, опирающиеся на одну и ту же дугу или равные дуги окружности, равны. 3.Вписанный в окружность угол равен половине центрального угла, опирающегося на ту же дугу, что и вписанный угол.   4*.Градусная мера угла, образованного хордой и касательной, имеющими общую точку на окружности, равна половине градусной меры дуги, заключенной между его сторонами. 5.Вписанный угол, опирающийся на диаметр, – прямой. Вершины всех прямых углов прямоугольных треугольников с общей гипотенузой лежат на одной окружности с диаметром, равным этой гипотенузе.	10. Дуга может измеряться в градусах, её величина равна величине соответствующего ей центрального угла. ˘ AB = <AOB. 11.Длина дуги окружности,содержащей n градусов, вычисляется по формуле: l =π r· n/180º, где r – радиус окружности. 12.Площадь секторавычисляется по формуле s = π R²n/360º, где R – радиус круга, n угловая величина дуги сектора.
Примечания	6*.Если вершина угла находится вне круга, а стороны пересекают окружность, то величина этого угла равна полуразности дуг, заключенных между точками пересечения сторон угла с окружностью. 7*.Если вершина угла находится внутри круга, а стороны пересекают окружность, то величина этого угла равна полусумме дуг, заключенных между точками пересечения сторон угла с окружностью. 8.Произведение отрезков секущих от данной точки до точки пересечения с окружностями, проведенных из одной точки к окружности есть величина постоянная. 9.Произведения отрезков пересекающихся хорд одной окружности, проходящих через одну точку, равны.

Задачи

1.Треугольник ABC вписан в окружность с диаметром CD. Хорда AB параллельна CD. Найдите AB, если AC = 4, СВ = 3см.

2.Из вершины тупого угла A треугольника ABC опущена высота AD. Из точки D радиусом, равным AD, описана окружность, пересекающая стороны треугольника AB и AC в точках M и N соответственно. Вычислите длину стороны AC, если заданы длины отрезков AB = c, AM = n, AN = m.

Таблица17

Геометрический объект	Вписанные четырехугольники	Вписанные многоугольники
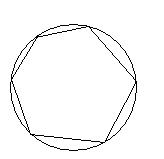
Определение	Если вершины четырехугольника лежат на окружности, то эта окружность описана около четырехугольника, а четырехугольник вписан в окружность.	Если вершины многоугольника лежат на окружности, то эта окружность описана около многоугольника, а многоугольник вписан в окружность
Изображение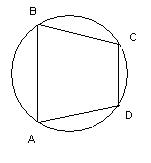
Свойства	1. Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма двух его противоположных углов равна 180º. 2. *Во вписанном четырехугольнике сумма произведений противоположных сторон равна произведению диагоналей (теорема Птолемея). 3. *Если около трапеции описана окружность, то она равнобедренная.	5. Около правильного многоугольника можно описать окружность.
Примечания	4.*Около четырехугольника ABCD можно описать окружность, тогда и только тогда, когда угол ABD равен углу ACD.

Задачи

1.Треугольник ABC вписан в окружность с диаметром CD. Хорда AB параллельна CD. Найдите AB, если AC = 4,

СВ = 3см.

2. Отрезки AK и СL биссектрисы углов A и C треугольника ABC пересекаются в точке O. Около четырехугольника BKOL описана окружность. Найдите величину угла B.

Решение

3.Из точки A, расположенной вне окружности, проведены две касательные AM и AN.

(M и N – точки касания) и секущая, пересекающая окружность в точках P и Q. L – середина отрезка PQ. <MLA= 65°. Найдите угол NLA.

4.Медианы AA₁ и BB₁ треугольника ABC пересекаются в точке M. Найдите AC, если длина третьей медианы равна m и точки C₁, B, A₁ и M лежат на одной окружности

Таблица 18

Геометрический объект	Описанные четырехугольники	Описанные многоугольники
Определение	Если стороны четырехугольника касаются окружности, то он описан около окружности, а окружность вписана в четырехугольник.	Если стороны многоугольника касаются окружности, то он описан около окружности, а окружность вписана в многоугольник.
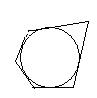
Изображение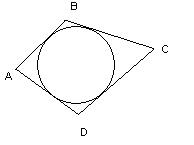
Свойства	1. Четырехугольник можно описать около окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.   2*.Если в равнобедренную трапецию вписана окружность, то ее средняя линия равна боковой стороне. 3. Радиус окружности, вписанной в трапецию равен половине ее высоты.	4*. Если в многоугольник с четным числом сторон можно вписать окружность, то суммы длин его сторон, взятых через одну, равны.
Примечания

Задачи

1.В равнобедренную трапецию вписана окружность. Точка касания делит боковую сторону на отрезки, отношение длин которых равно 3:1. Найдите острый угол трапеции.

Решение

2.Равнобедренная трапеция при основании имеет угол 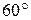. Найдите отношение радиусов описанной около нее и вписанной в нее окружностей.

3. Около окружности описана равнобедренная трапеция с острым углом 60°. Найти отношение длин оснований.

Решение

Таблица19

Геометрический объект	Многоугольник	Правильный многоугольник
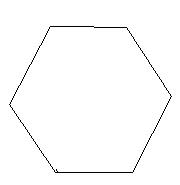
Определение	Многоугольником называется часть плоскости, ограниченная замкнутой ломаной линией. Многоугольник называется выпуклым, если он целиком лежит по одну сторону от каждой прямой, содержащей его стороны.	Выпуклый многоугольник называется правильным, если всеего стороны равны и все углы равны
Изображение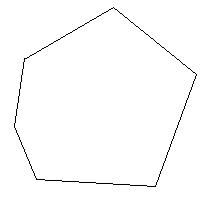
Свойства	1. Сумма внутренних углов любого n-угольника вычисляется по формуле 180º(n -2). 2 .Суммавнешних углов любого много угольника, взятых по одному при каждой вершине, равна 360º. 3.Число диагоналей n-угольника, выходящих из одной вершины, равно n-3. 4.Числовсех диагоналей n- угольника равно n(n-3)/2.	5. Около любого правильного многоугольника можно описать окружность 6. В любой правильный многоугольник можно вписать окружность
Примечания		7.Можно найти сторону, периметр и площадь правильного многоугольника через радиус описанной окружности. В любой правильный многоугольник можно вписать окружность   8.Можно найти сторону, периметр, площадь правильного многоугольника через радиус вписанной окружности

Задачи

1.Может ли n- угольник иметь количество диагоналей, равное 4,5n(n-1)?

.

2.Число диагоналей n - угольников 3 раза больше числа его сторон. Сколько сторон имеет многоугольник?

Решение

3.Вокруг квадрата описана окружность, а около нее описан правильный шестиугольник. Определить площадь этого шестиугольника, если сторона квадрата равна a.

Таблица20

Геометрический объект	Площади фигур
Определение	a) Площадь многоугольника положительна. b) Если многоугольник состоит из неперекрывающихся многоугольников, то его площадь равна сумме площадей составляющих его многоугольников. c) Равные фигуры имеют равные площади. d) Площадь квадрата со стороной 1 равна 1.
Изображение
Свойства	Площадь треугольника: 1. a)Площадь прямоугольного треугольника равна половине произведения его катетов: S =1/2ab. b)Площадь прямоугольного треугольника равна половине произведения его гипотенузы и высоты, проведенной к гипотенузе S =1/2ch. c). Высота, проведенная к гипотенузе, равна ab/c. 2. Площадь равностороннего треугольника вычисляется по формуле: S = a²√3/4; 3. Площадь произвольного треугольника равна половине произведения стороны и высоты, проведенной к этой стороне;   4. Площадь треугольника можно вычислить по формуле: S = 1/2absin<C.   5. Площадь треугольника можно вычислить по формуле Герона S =√p (p-a)(p-b)(p-c), где p = (a+b+c):2.   6. Площадь треугольника равна произведению его полупериметра и радиуса вписанной в этот треугольник окружности. 7. Медиана треугольника делит его на два равновеликих треугольника.   8. *Отрезок прямой от вершины угла треугольника до точки на противоположной стороне делит площадь треугольника на части, пропорциональные отрезкам, на которые делится сторона этой прямой. 9. *Отношение площадей треугольников, имеющих общий угол, равно отношению произведений сторон треугольников, заключающих этот угол. 10. **Площадь треугольника равна произведению полупериметра ортоцентрического треугольника и радиуса описанной окружности.   Площадь параллелограмма 11. S = ah, где a – сторона параллелограмма, а h – высота, проведенная к этой стороне. 12. Площадь параллелограмма равна половине произведения его диагоналей и синуса угла между диагоналми. Площадь трапеции 13. a)Площадь трапеции равнапроизведению полусуммы её оснований и высоты, т.е. S =(a +b)h/2. b) отношение площадей треугольников, на которые трапеция разбивается одной из диагоналей равно отношению оснований. 14*.Площадь трапеции равна произведению боковой стороны и отрезка перпендикуляра, проведенного к этой стороне из середины другой боковой стороны. 15.*Площадь равнобедренной трапеции с перпендикулярными диагоналями равна квадрату ее высоты. 16.* Площади двух треугольников, образованных диагоналями трапеции прилежащих к ее боковым сторонам, равны. Площадь ромба 17.Площадь ромба равна произведению квадрата стороны и синуса его угла.   18.Площадь ромба равна половине произведения его диагоналей.   Площадь прямоугольника 19.Площадь прямоугольника равна произведению длин длины двух его сторон (длины и ширины). 20. Площадь прямоугольника равна половине произведения квадрата его диагонали и синуса угла между диагоналями. Площадь квадрата 21.Площадь квадратаравна квадрату его стороны. 22.Площадь квадрата равна половине квадрата его диагонали. S=a²=1/2d².
Примечания

Задачи

1.Длины оснований трапеции ABCD равны 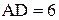см и 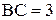см, O – точка пересечения ее диагоналей. Площадь треугольника 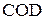равна 2 см ². Найдите высоту трапеции.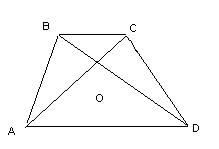

2.В трапеции с основаниями AD и BC точка пересечения диагоналей делит диагональ AC на отрезки длиной 6 см и 3 см. Площадь треугольника 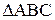равна 12 см² . Найдите площадь трапеции.

3.Радиус вписанной в прямоугольный треугольник окружности равен 2 м, а гипотенуза в точке касания делится на отрезки длины 4 м и 6м. Найдите площадь этого треугольника.

4.В равнобедренную трапецию вписана окружность радиуса 6 см. Точка касания делит боковую сторону на отрезки, отношени