Аксиома Больцано-Вейерштрасса и теорема о стягивающейся системе отрезков

В теории пределов очень важно одно свойство действительных чисел, которое обычно принимают за аксиому.

Аксиома Больцано-Вейерштрасса:
всякая монотонная ограниченная последовательность имеет предел.

Данная аксиома обеспечивает только существование предела и ничего не говорит о его величине. Однако иногда достаточно знать это, чтобы его найти.

Рассмотрим пример:

Пример 34. Дана последовательность 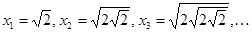. Докажем, что она сходится и найдем ее предел.

Для этой последовательности справедливо равенство . (*)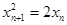

Для доказательства существования предела применим аксиому Больцано-Вейерштрасса. По индукции можно доказать, что 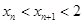. Поэтому последовательность 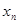монотонна и ограничена.

Если последовательность 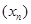имеет предел 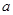, то левая часть равенства (*) стремится к , а правая - к 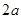. Получаем 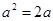, 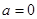или 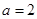. Очевидно, 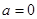не является пределом последовательности 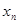. Значит, .

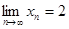Аналогично можно доказать, что 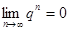, если .

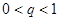►Теорема 5. Пусть даны две последовательности и такие, что:

1) последовательность монотонно не убывает: ;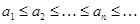

2) последовательность монотонно не возрастает ;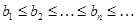

3) для любого выполняется неравенство ;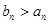

4) разность 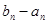стремится к нулю при , .

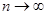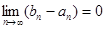Тогда существует число 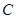, являющееся общим пределом этих последовательностей: 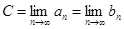, причем, для всех выполняется неравенство .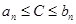

Доказательство: рассмотрим последовательность , она не убывает и ограничена сверху: 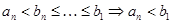, значит у нее есть предел (аксиома Больцано – Вейерштрасса), обозначим его .

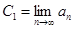Аналогично, для : она не возрастает и ограничена снизу: 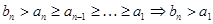, значит, в силу аксиомы Больцано – Вейерштрасса, последовательность имеет предел, обозначим его .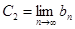

Рассмотрим условие 4): 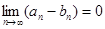; поскольку существует предел каждого слагаемого, можно применить теорему о пределе суммы (разности):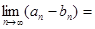 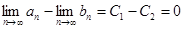, значит, 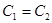и последовательности имеют общий предел .

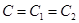Пример 35. Последовательности и определяются рекуррентными соотношениями 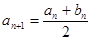, , 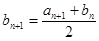причем 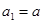; 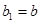где 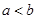. Докажите, что они имеют общий предел.

Доказательство: из условий следует, что 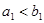; докажем, что 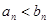, используя метод математической индукции. Пусть для , где 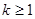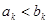, тогда 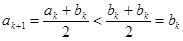; значит, 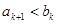; ; 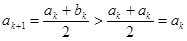з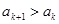начит, ; ; значит, 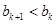; ; 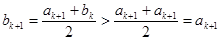значит, 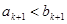; отсюда следует не только тот факт, что 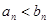, но и возрастание последовательности , убывание последовательности .

Рассмотрим 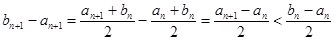, поэтому 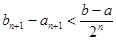и .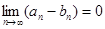

В силу ►Теорема 5 последовательности и имеют общий предел.

►Теорема 5 имеет следующий геометрический смысл. Рассмотрим отрезки 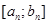. Из условий следует, что отрезок 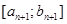является частью отрезка 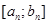(так как 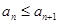и 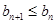), кроме того, длины отрезков 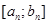стремятся к нулю, когда 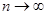. Неравенство 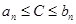означает, что точка принадлежит всем отрезкам .

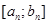Таким образом, геометрическая формулировка ►Теорема 5 такова:

►Теорема 6. Пусть последовательность отрезков 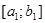; ; 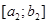… ; … 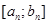такова, что:

1) каждый следующий отрезок является частью предыдущего: ;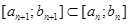

2) длины отрезков стремятся к нулю при , .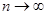

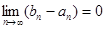Тогда существует единственная точка 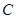, принадлежащая всем этим отрезкам, причем .

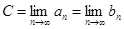Говорят, что система отрезков 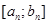стягивается в точку 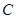, поэтому ►Теорема 6 называют теоремой о стягивающейся системе отрезков. Эта теорема играет существенную роль в теории действительных чисел.