Методы анализа предметной области при нечетких условиях выбора решений

6.1. Нечеткая логика – математические основы

Классические теорию множеств и формальную логику обобщают математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic). Эти понятия впервые введены Лотфи Заде (Lotfi Zadeh) в 1965 г., что было вызвано появлением нечетких и приближенных рассуждений при описании процессов и систем.

Примеры нечетких понятий: человек высокого роста; горячая вода; темно-зеленый цвет.

Первоначально были получены результаты в нечетком управлении техническими системами, в построении экспертных систем на нечеткой логике. Такие экспертные системы нашли применение в экономике и медицине. В дальнейшем, с конца 80-х годов, созданы пакеты программ для построения нечетких экспертных систем, а применение нечеткой логики распространилось на финансовые, транспортные системы и производственную сферу.

Начало создания математического аппарата - формализация предметной области; например, формализация определения "горячая вода". Пусть переменная x (область рассуждений) – температура воды в градусах Цельсия, диапазон шкалы от 0 до 100 градусов. Нечеткое множество для понятия "горячая вода" запишем следующим образом:

C={0/0; 0/10; 0/20; 0,15/30; 0,30/40; 0,60/50; 0,80/60; 0,90/70; 1/80; 1/90; 1/100}, где второе число означает элемент множества – температуру воды, а первое – степень соответствия данного элемента понятию “горячая вода”.

Вода с температурой 60º С относится к множеству "горячая" со степенью принадлежности 0,80. Для одних целей вода при этой температуре может быть горячей, для других – нет, в чем и проявляется нечеткость задания множества.

С учетом изложенного, нетрудно понять основные положения математики нечетких множеств, созданной, Л. Заде (1,2).

В обычной теории множеств исходное понятие - принадлежность хÎ А элемента х некоторого обычного множества Х к подмножеству АÌХ. Эту принадлежность можно описать и характеристической функцией m A (х), значение которой указывает, является ли (да или нет) х элементом А:

m A (х) = 1, если хÎ А,

m A (х) = 0, если хÏ А.

В гуманитарных областях знания такое определение недостаточно в ситуациях, описываемых нечетко определенными понятиями типа "множество богатых людей", "множество хороших законов", "множество чисел значительно больше 100", и т. д. Здесь введенное выше определение (дихотомия функции принадлежности) не разрешает любому элементу одновременно принадлежать или, в некотором понимании, не принадлежать данному множеству. Поэтому, дихотомию функции принадлежности (т.е. определение, что элемент множества обязательно либо принадлежит множеству, либо нет) следует отвергнуть.

Л.Заде в основу теории нечетких множеств положил тезис, что элементы множества, могут обладать общим свойством в различной степени а потому принадлежать данному множеству с различной степенью. При этом высказывание "элемент принадлежит множеству А" требует указания, в какой степени реализуется такая принадлежность. Множество степеней принадлежности может оцениваться на бесконечной шкале действительных чисел от 0 до 1, или на части чисел интервала [0,1], также и на конечной шкале. Например, объект, определяемый выражением А = {(x₁ | 0,2), (x₂ | 0), (x₃ | 0,3), (x₄ | 1), (x₅ | 0,8)}, где х _i - элемент универсального множества Х, а число после вертикальной черты - значение характеристической функции на этом элементе, будем называть нечетким подмножеством А множества Х.

Это нечеткое подмножество А содержит в малой степени х₁; не содержит х₂; содержит х₃ в несколько большей степени, чем х₂; полностью содержит х₄ и в существенной степени х₅. Итак, А - нечеткое подмножество, если в нем есть хоть один элемент х, который принадлежит А со степенью, отличной от 1.

Определим понятие нечеткого множества строго. Пусть Х – не обязательно счетное множество, и х - его элемент. Тогда нечеткое подмножество А множества Х есть множество упорядоченных пар {(x, µ A(х))} для всякого х_i из множества Х, где µ A(х) - характеристическая функции принадлежности со значениями во множестве М (например, из интервала [0,1]), указывающая степень принадлежности элемента х подмножеству А. Если в М есть только два элемента, а не интервал значений, т.е. М = {0,1}, то "нечеткое подмножество" становится "четким" или обычным подмножеством. Итак, нечеткое подмножество обобщает понятие обычного подмножества.

Например, пусть N - подмножество целых чисел: {0, 1, 2,...}, и А = {(0| 1), (1| 0,8), (2| 0,6), (3| 0,4), (4| 0,2), (5| 0),...} - нечеткое подмножество "небольших" натуральных чисел, где функциональные значения µ A(х), где х = 0, 1, 2,... заданы субъективно. Видно, что 0 полностью принадлежит А, 1 принадлежит А со степенью 0,8, и т.д. Совокупность этих чисел, стоящих за вертикальной чертой (т.е. 0,8, 0,6, 0,4, 0,2, 0.) и является характеристической функцией принадлежности µ A(х).

Существует ряд типовых форм кривых для задания функций принадлежности; наиболее применимы треугольная, трапецеидальная и гауссова функции принадлежности.

Треугольная функция принадлежности определяется тремя числами (a,b,c), и ее значение в точке x вычисляется согласно выражению

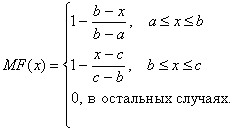
и его изображению (рис. 6.1).

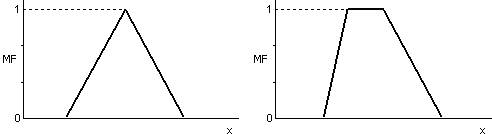
Рис. 6.1. Треугольная и трапецеидальная функции принадлежности.

В случае (b-a)=(c-b) треугольная функция принадлежности симметрична и задается однозначно двумя параметрами из тройки (a,b,c)., а для задания трапецеидальной функции принадлежности нужно четыре числа (a,b,c,d) (рис. 6.1.):

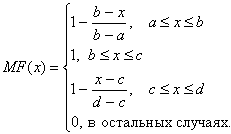
При (b-a)=(d-c) трапецеидальная функция принадлежности тоже симметрична.

Функция принадлежности гауссова типа двухпараметрическая и описывается формулой

,

где параметр c означает центр нечеткого множества, а σ характеризует отклонение от центра. График функции для σ = 4 приведен на рис. 6.2.

Рис. 6.2. Функция принадлежности гауссова типа.

Определим операции пересечения ∩, объединения U и дополнения - нечетких множеств. Пусть Х - множество и А и В два нечетких подмножества Х. Тогда для каждого х Î Х:

A Î B, если µ A (х) < µ B (х),

A = B, если µ A (х) = µ B (х).

µ (A U B (х)) = max(µ A (х), µ B (х)),

µ (A ∩ B (х))= min(µ A (х), µ B (х)),

µ(A’ (х)) = 1- µ A (х),

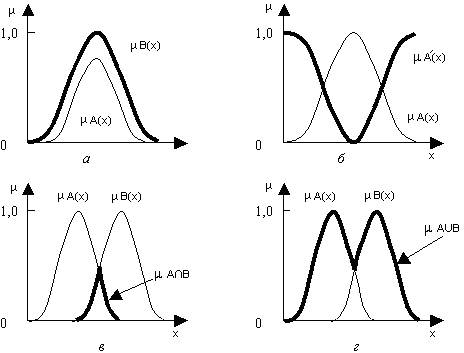
Рисунок 6.3. – Основные операции над нечеткими множествами.

Например, для единичного множества Е = {(x1| 1), (x2| 1), (x3| 1), (x4| 1); (x5| 1), (x6| 1), }, а для пустого Ǿ = {(x1| 0), (x2| 0), (x3| 0), (x4| 0); (x5| 0), (x6| 0). }. Легко получить и другие известные из теории множеств законы для нечетких множеств.

Пусть А подмножество Е, например:

А = {(x1| 0,2), (x2| 0,7), (x3| 1), (x4| 0); (x5| 0), (x6| 0).}.

Тогда его дополнение будет А’ = {(x1| 0,8), (x2| 0,3), (x3| 0), (x4| 1); (x5| 1); (x6| 1).}.).

Пусть В также подмножество Е, например:

В= {(x1| 0,6), (x2| 0,4), (x3| 0), (x4| 0,1); (x5| 0,3), (x6| 0,7).}.

Тогда верны следующие равенства:

А ∩ Е = А или А ∩ 1 = А;

А U Е = Е или А U 1 = 1,

А ∩ Ǿ = Ǿ;

А U Ǿ = А.

С = A U B = {(x1| 0,6), (x2| 0,7), (x3| 1,0), (x4| 0,1); (x5| 0,3), (x6| 0,7).}.

С = A ∩ B ={(x1| 0,2), (x2| 0,4), (x3| 0), (x4| 0); (x5| 0), (x6| 0).}.

Важно, что. А ∩ А’ не равно 1, т.к. А ∩ А’ = {(x1| 0,8), (x2| 0,7), (x3| 1), (x4| 1)}.

Понятие истинности само является нечетким, поэтому используются нечеткие подмножества с нечеткими функциями принадлежности. Если А - нечеткое подмножество универсального множества Х, то значениями функций принадлежности будут нечеткие подмножества из интервала [0,1]. Такие нечеткие подмножества относят к т.н. второму типу. Более строго: нечеткое подмножество А типа 2 в Х характеризуется нечеткой функцией принадлежности µ A(х):

µ A (х): Х → [0,1] ^j.

При этом значение µ A(х) называется нечеткой степенью и является нечетким подмножеством в [0,1], а в качестве j берется также [0,1]. Тогда, если нечеткое подмножество типа 1 задано функцией принадлежности µ A(х): Х→[0,1], то подмножество типа 2 задается функцией принадлежности µ A(х): Х→F([0,1]), где

F([0,1]) = {f: [0,1] → [0,1]}. Это значит, что функция принадлежности элементов подмножества к множеству сама может быть нечеткой. Аналогично определяются нечеткие подмножества типа 3, 4 и т.д.

Для работы с нечеткими рассуждениями и выводами введены понятия нечеткой и лингвистической переменных.

Лингвистическая переменная. (Linguistic variable) принимает значения понятий (фраз) естественного языка и используется при описании объектов и процессов нечеткими множествами; так, лингвистическая переменная “Температура” может принимать значения “горячо”, “тепло”, “холодно”.

Нечеткая переменная описывается тройкой (N,X,A), где N - название переменной, X – область рассуждений (универсальное множество), A – нечеткое множество на X. Лингвистическая переменная принимает значения нечетких переменных, т.е. нечеткая переменная занимает уровень ниже лингвистической переменной. Структура лингвистической переменной:

· название N;

· множество значений (базовое терм-множество) T. Элементы T суть названия нечетких переменных, обычно термов в лингвистической переменной не более 7;

· универсальное множествоX;

· синтаксическое правило G для генерирации новых термов из слов естественного или формального языка;

· семантическое правило P, ставящее в соответствие каждому значению лингвистической переменной нечеткое подмножество множества X.

При аналие предметной области при создании ИС с нечеткими параметрами определяют эти переменные.

Нечеткое понятие "Температура воды" совпадает с названием лингвистической переменной (N). Ее базовое терм-множество T имеет три нечетких переменных: "Низкая", "Средняя", "Высокая"; в области рассуждений в виде X=[0;100] (градусов) построим функции принадлежности для каждого терма из T.

Изображения функций принадлежности для каждого терма из T обычно даются на одном графике. На рис. 6.4. приведен пример лингвистической переменной "Температура воды",

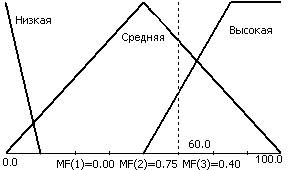
Рис.6.4. Описание лингвистической переменной "Температура воды".

В основе нечеткого логического вывода лежит база правил, содержащая функции принадлежности для лингвистических термов и нечеткие высказывания в форме "Если-то". Требуется соблюдение ряда условий:

• Есть не менее одного правила для каждого лингвистического терма выходной переменной.
• Для каждого терма входной переменной есть хотя бы одно правило, в которое этот терм входит как предпосылка (левая часть правила).

Логический вывод включает до 4 этапов: приведение к нечеткости (фазификация), нечеткий вывод, композиция и приведение к четкости (дефазификация), рис. 6.5.).

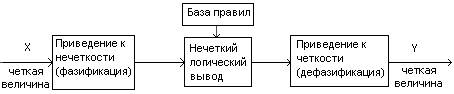
Рис. 6.5. Этапы нечеткого логического вывода.

Алгоритмы нечеткого вывода различаются главным образом видом используемых правил, логических операций и разновидностями методов дефазификации. Рассмотрим подробнее нечеткий вывод по наиболее распространенному механизму Эбрахима Мамдани, где использована минимаксная композиция нечетких множеств.