Расчет показателей надежности восстанавливаемых систем

Изучение вероятностных процессов занимает большое место в анализе и обеспечении надежности сложных систем, так как их функционирование представляет собой реализацию вероятностных процессов. Вероятностным (или случайным) процессом называется случайная функция, аргументом которой является время. Чтобы охарактеризовать вероятностный процесс, необходимо указать тип процесса и его числовые характеристики. Существует большое количество различных типов вероятностных процессов. Поскольку функционирование сложных систем, как правило, сопровождается простейшими потоками отказов и восстановлений (простейшим называется поток, обладающий свойством ординарности, стационарности и отсутствием последствий), наиболее подходящим для описания таких процессов является Марковский процесс. Кроме того, время работы до отказа и время восстановления имеют экспоненциальный характер.

Марковский процесс – процесс, у которого для каждого момента времени вероятность любого состояния системы в будущем зависит только от ее состояния в настоящий момент времени и не зависит от того, каким образом система пришла в это состояние. Характеристику процесса удобно сопровождать графическим изображением (графом состояний и переходов). С его помощью изображаются процессы перехода системы из одного состояния в другое в случайный момент времени. Граф переходов может быть представлен либо матрицей переходов, либо системой уравнений.

Одним из основных (инженерных) методов является метод, основанный на использовании понятия графов переходов между состояниями [3].

Этот метод распадается на два вида:

1) граф интенсивности перехода. Основное условие использования этого метода – это то, что потоки событий простейшие, т.е. отказы и восстановления описываются экспоненциальными законами;

2) метод переходных матриц вероятностей. В принципе, может быть любой закон распределения вероятности, но инженерное использование его проблематично.

Рассмотрим функционирование восстанавливаемой системы при следующих предположениях:

1) поток отказов носит пуассоновский характер и интенсивность отказов равна λ;

2) время восстановления системы является случайной величиной, распределенной по экспоненциальному закону

,

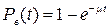где µ - интенсивность восстановления;

3) система может находиться в двух состояниях: состоянии 1 (работоспособности) и 2 (ремонта).

Поведение системы с точки зрения работоспособности опишем графом переходов.

На рисунке 4.19 кружки с номером означают состояние системы, а стрелки (дуги) направление переходов системы и вероятности этих переходов за бесконечно малый интервал времени. Вероятность переходов в силу сделанных предложений и свойства показательности закона надежности не зависят от времени. Введем вероятности нахождения системы в состоянии 1 и 2 как Р₁(t) и Р₂(t). Очевидно, что Р₁(t) + Р₂(t)=1 для любого момента времени.

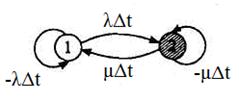
Рисунок 4.19 – Граф переходов объекта

Рассмотрим поведение системы в интервале времени [0,t+Δt]. Тогда система в момент t+Δt будет находиться в состоянии 1, если она в момент времени t находилась в этом состоянии, и за время Δt не наблюдалось отказов, а также если система в момент времени t находилась в состоянии 2, и за время Δt был закончен ее ремонт. Тогда по формуле полной вероятности

.

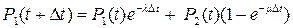Так как е^-λΔt≈1- λΔt, е^-µΔt≈ µΔt, то

.

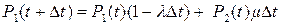Аналогичные рассуждения приводят к уравнению

.

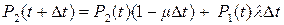Предельный переход при Δt→0 дают дифференциальные уравнения, описывающие поведение системы во времени:

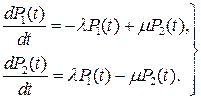(4.23)

Вышеприведенное уравнение получило название дифференциальное уравнение Колмогорова-Чепмена.

Произведем переход к изображению по Лапласу и определим Р₁(s).

Решение уравнения можно получить, используя преобразования Лапласа. Основные соотношения между значениями f(t) и f(s) приведены ниже:

f(t)	f(s)=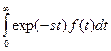
	1/s
e±at	(1/s±a)
f(t)	F(s)
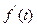
	sF(s)

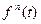
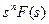
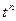
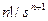
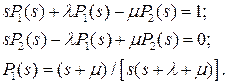
Для того чтобы привести выражение Р₁(t) к табличному, умножим и разделим правую часть на постоянную величину (λ+μ). В результате получим

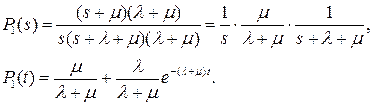(4.24)

Выражение справа состоит из постоянной и убывающей с течением времени частей. Постоянную часть называют стационарным коэффициентом готовности.

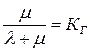- стационарный коэффициент готовности.

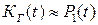при .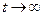

На рисунке 4.20 представлена функция готовности.

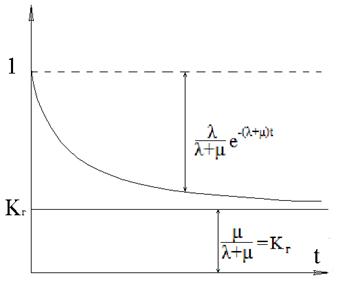
Рисунок 4.20 – Функция готовности

Граф переходов системы с учетом восстановления в общем случае изображен на рисунке 4.21.

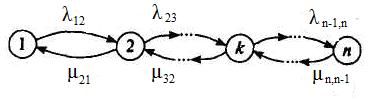
Рисунок 4.21 – Граф переходов системы с восстановлением

Для получения системы дифференциальных уравнений непосредственно по виду графа переходов используют следующие правила:

1 Для каждого из возможных состояний системы записывается уравнение, в левой части которого - , а справа - столько слагаемых, сколько стрелок графа соприкасается с данным состоянием.

2 Если стрелка направлена в данное состояние, то перед слагаемым ставится плюс, если стрелка направлена из данного состояния - минус.

3 Каждое из слагаемых будет равно произведению интенсивности перехода из данного состояния (либо в данное состояние) на вероятности состояния, из которого выходит стрелка.

4 Вероятность нулевого состояния определяется выражением

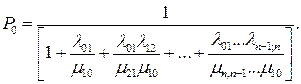
5 Вероятность каждого из состояний определяется выражением

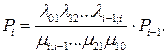(4.25)

Расчет надежности, связанный с решением дифференциальных уравнений, достаточно трудоемок. Поэтому разработаны приемы, упрощающие расчет.

Исследования характеристик надежности, формируемых под воз­действием потока отказов и восстановления, позволяют сделать вывод о том, что при существующих соотношениях λи µ сравнительно быстро наступает период установившегося режима, когда вероятности состояний объекта становятся постоянными, т.е. dP_j(t)/dt =0. Тогда система дифференциальных уравнений (4.23) становится системой алгебраических уравнений:

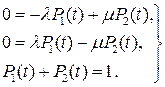(4.26)

Решив систему (4.26), получаем стационарный коэффициент го­товности

.

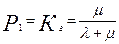Для облегчения расчетов можно пользоваться следующим правилом. Если состояния заданы графом, имеющим вид (рисунок 4.21), тогда расчет надежности производится в следующей последовательности.

Записать уравнения состояний для каждого состояния по правилу: в левой части написать нуль, а правой части — столько членов, сколько стрелок связано с данным состоянием (каждой стрелке должно
соответствовать слагаемое, представляющее собой произведение интен­сивности перехода на вероятность того состояния, из которого происходит переход; выходящей стрелке соответствует минус, входящей - плюс).

Вероятности каждого из состояний определяют выражениями

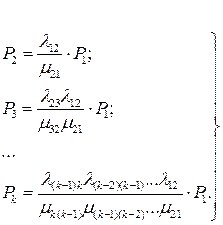(4.27)

Запись для вероятности k-го состояния в (4.27) следует читать так: вероятность k-го состояния равна произведению коэффициента на вероятность первого состояния Р₁. Коэффициент равен дроби, числитель которой – произведение интенсивностей отказов, стоящих над стрелками, идущими вправо до k-го состояния, а знаменатель – произведение интенсивностей восстановлений, стоящих над стрелками, идущими влево от k-го состояния до первого.