Бесконечно большие функции и их свойства

Определение. Функция y = F(x) называется бесконечно большой (б.б.) при x® a, если

.

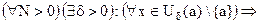
Это обозначается символом , хотя предел этой функций при не существует.

Пример. Функция является б.б. функцией при , так как

.

Очевидно, что любая б.б. функция не ограничена в окрестности точки .

Если и в некоторой окрестности точки а функция 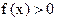(соответственно ), то еще пишут (соответственно ).

Отметим следующие свойства б.б. функций.

1) Сумма двух б.б. одного знака при является б.б. при .

2) Сумма б.б. функции при и ограниченной в окрестности точки а функции является б.б. при .

Пример. ,так как х- есть б. б. при , а 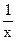б. м., следовательно, ограниченная функция при .

3) Если б. б. при , а в некоторой окрестности точки а, то функция является б. б. при . В частности, произведение двух б. б. и произведение б. б. на функцию, имеющую ненулевой предел, является б. б.

Пример. , так как х – б.б. и .

4) Если б. б. при , то б.м. при .

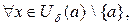5) Если б.м. при и при то является б.б. при .

Пример: , так как б. б. одного знака при .

Сравнение бесконечно малых и бесконечно больших

Определение. Бесконечно малая называется б.м. высшего порядка малости по сравнению с б.м. при в случае, если найдётся б.м. при такая, что . Соответствующее обозначение .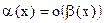

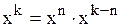Пример: При , так как и 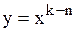есть б.м. при .

При :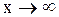

Определение. Бесконечно малые при называются эквивалентными, если . Обозначение ~ . Подобное определение даётся и для б.б. функции.

Пример. Б.м. эквивалентны при , это следует из первого замечательного предела.

Это отношение эквивалентности удовлетворяет трём свойствам

1) ~ ;

2) ~ ~ ;

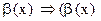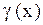3) Если ~ и ~ , то ~ .

Теорема. Из ~ следует, что .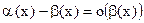

Теорема. Пусть есть б. м. при , тогда:

1) ;

2) ~ ;

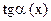3) ~ ;

4) ~ ;

5) ~ ;

6) ~ , ;

7) ~ .

Эти эквивалентные б.м. позволяют более просто вычислять некоторые пределы с помощью следующей теоремы.

Теорема. Пусть ~ 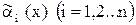при , тогда

.

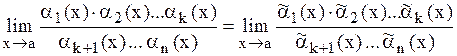При этом оба записанных предела существуют одновременно. Если одно из выражений б. б., то другое также является б. б.

Пример. ,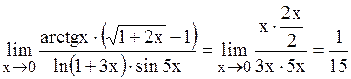

так как ~ ~ ~ ~ .