Коефіцієнтами

Лінійне неоднорідне диференціальне рівняння 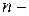го порядку зі сталими коефіцієнтами має вигляд

. (1)

Кожному такому рівнянні відповідає лінійне однорідне рівняння

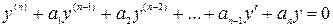. (2)

Теорема. Загальний розв’язок в області рівняння (1) з неперервною правою частиною дорівнює сумі загального розв’язку 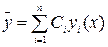відповідного однорідного рівняння і якого-небудь частинного розв’язку 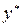неоднорідного рівняння, тобто .

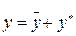Розглянемо два методи розв’язання неоднорідних рівнянь.

Метод невизначених коефіцієнтів. Цей метод можна використовувати якщо права частина рівняння (1) має вигляд

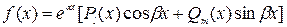, (3)

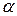де і 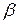дійсні числа, а 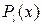і – многочлени відповідно – 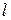-й і -й степенів з дійсними коефіцієнтами, то частинний розв’язок, рівняння (1) шукається у вигляді

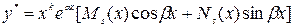, (4)

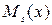де і 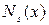– многочлени 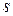-й степені ( 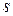- найбільша із степенів 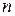і ) з невизначеними коефіцієнтами, а 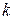– кратність, з| якою число входить до числа коренів характеристичного рівняння.

Для того, щоб знайти коефіцієнти многочленів 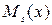і 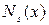, шуканий частинний розв’язок (4) підставляють в ліву частину диференціального рівняння (1) і виконують відповідні спрощення; потім в одержаній тотожності прирівнюють коефіцієнти при подібних членах в лівій і правій частинах, що дає систему лінійних рівнянь щодо невідомих коефіцієнтів, з якої вони визначаються.

Вкажемо вигляд частинного розв’язку для деяких окремих випадків функції (3):

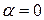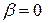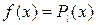1) якщо , , то і частинний розв’язок шукається у вигляді

,

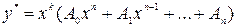де 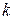– кратність, з якою нуль входить до числа коренів характеристичного рівняння; 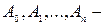невідомі коефіцієнти.

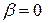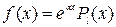2) якщо , то і частинний розв’язок шукається у вигляді

,

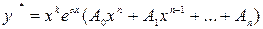де 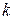– кратність, з якою 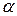входить до числа коренів характеристичного рівняння;

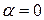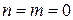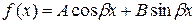3) якщо , , то і частинний розв’язок шукається у вигляді

,

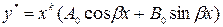де 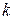– кратність, з якою 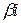входить до числа коренів характеристичного рівняння.

В тому випадку, якщо права частина рівняння (1) є сума функції вигляду (3), тобто

,

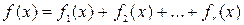потрібно заздалегідь знайти частинні розв’язки 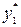, ,…, , 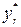відповідні функціям 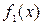, ,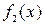…, 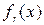. Тоді частинний розв’язок рівняння (1) запишеться у вигляді.

.

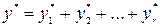Метод варіації довільних сталих. Більш загальним методом розв’язання лінійного неоднорідного рівняння (1) є метод варіації довільних сталих. Приведемо його для лінійного неоднорідного рівняння другого порядку:

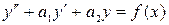. (5)

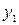Хай і 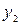– лінійно незалежні частинні розв’язки відповідного однорідного рівняння

. (6)

Тоді загальний розв’язок неоднорідного рівняння (5) слід шукати у вигляді

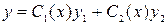, (7)

де функці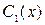ї і 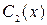визначаються з системи рівнянь:

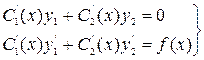(8)

Після розв’язання системи рівнянь (8), знаходимо

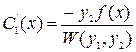, , (9)

де - визначник Вронського, складений для розв’язків 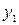і .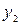

Інтегруємо рівності (9) і одержуємо

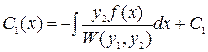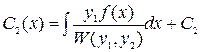, . (10)

Далі після підстановки знайдених функцій 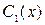і 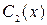в співвідношення (7), одержимо загальний розв’язок лінійного неоднорідного рівняння (1).