 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Векторная алгебра 3 страница
|
|
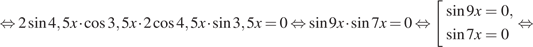
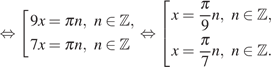
Однако из полученных серий решений следует исключить числа вида 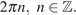
Таким образом, решения заданного уравнения – числа вида 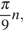
 за исключением чисел вида
за исключением чисел вида 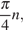 где
где 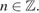
б) Выборку корней будем осуществлять путем перебора целых значений 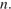
Из серии корней 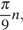 отличных от
отличных от  Чтобы найти наименьший искомый корень из этой серии решим неравенство
Чтобы найти наименьший искомый корень из этой серии решим неравенство  в целых числах. Получим:
в целых числах. Получим: 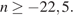 Отсюда ясно, что искомый наименьший корень вычисляется по формуле
Отсюда ясно, что искомый наименьший корень вычисляется по формуле 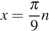 при
при  Далее, каждый следующий корень получим путем прибавления к нему числа
Далее, каждый следующий корень получим путем прибавления к нему числа  Результаты будем заносить в таблицу. Посторонние корни по ходу будем отсеивать, учитывая условие
Результаты будем заносить в таблицу. Посторонние корни по ходу будем отсеивать, учитывая условие 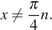



Аналогично найдем корни из серии  отличные от
отличные от 



Таким образом, мы нашли 42 корня, принадлежащие заданному отрезку.
Замечание.
Запись множества корней заданного уравнения может выглядеть так: 
Ответ: а) 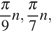 за исключением чисел вида
за исключением чисел вида 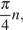 где
где 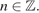 б) всего 42 корня (см. таблицу).
б) всего 42 корня (см. таблицу).
51. C 2 № 505174. В правильной треугольной пирамиде SABC с основанием ABC боковое ребро равно 3, а сторона основания равна 2. Найдите расстояние от вершины A до плоскости SBC.
Решение.
Пусть SO – высота пирамиды. Тогда

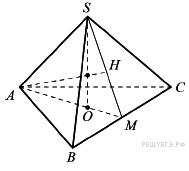
Пусть V – объём пирамиды, тогда 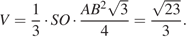
С другой стороны, 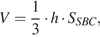 где h – искомое расстояние.
где h – искомое расстояние.
В треугольнике SBC высота SM равна 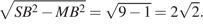
Площадь треугольника SBC равна  Получаем, что
Получаем, что
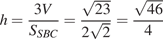
Ответ: 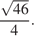
52. C 2 № 504416. В правильной треугольной пирамиде SABC боковое ребро SA = 5, а сторона основания AB = 4. Найдите площадь сечения пирамиды плоскостью, проходящей через ребро AB перпендикулярно ребру SC.
Решение.
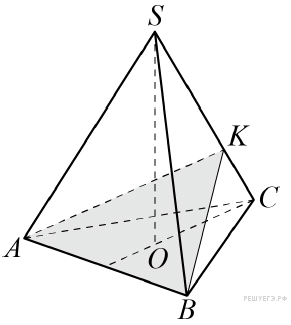 В треугольнике BCS проведём высоту BK, тогда искомое сечение — треугольник ABK. Пусть Q — площадь треугольника ABK. Сечение из условия разбивает пирамиду на тетраэдры CAKB и SAKB. Их суммарный объём
В треугольнике BCS проведём высоту BK, тогда искомое сечение — треугольник ABK. Пусть Q — площадь треугольника ABK. Сечение из условия разбивает пирамиду на тетраэдры CAKB и SAKB. Их суммарный объём
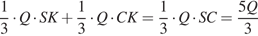
равен объёму пирамиды.
Пусть — SO высота пирамиды. В треугольнике SCO имеем:
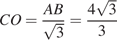
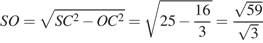
Объём пирамиды SABC равен
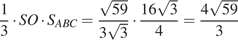
Приравнивая два найденных значения для объёма, получаем
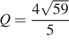
Ответ: 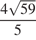 .
.
53. C 2 № 501945. В правильной четырёхугольной пирамиде 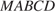 с вершиной
с вершиной 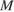 стороны основания равны
стороны основания равны 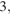 а боковые рёбра равны
а боковые рёбра равны 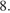 Найдите площадь сечения пирамиды плоскостью, проходящей через точку
Найдите площадь сечения пирамиды плоскостью, проходящей через точку 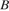 и середину ребра
и середину ребра 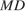 параллельно прямой
параллельно прямой 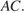
Решение.
 Пусть точка
Пусть точка 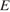 — середина ребра
— середина ребра 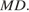 Отрезок
Отрезок  пересекает плоскость
пересекает плоскость 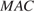 в точке
в точке 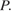 В треугольнике
В треугольнике 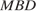 точка
точка 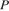 является точкой пересечения медиан, следовательно,
является точкой пересечения медиан, следовательно, 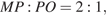 где
где  — центр основания пирамиды. Отрезок
— центр основания пирамиды. Отрезок 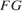 параллелен
параллелен 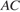 и проходит через точку
и проходит через точку 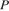 (точка
(точка 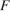 принадлежит ребру
принадлежит ребру 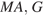 — ребру
— ребру 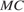 ), откуда
), откуда
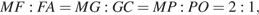
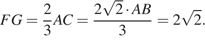
Четырёхугольник 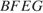 — искомое сечение. Отрезок
— искомое сечение. Отрезок  — медиана треугольника
— медиана треугольника 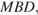 значит,
значит,

Поскольку прямая 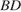 перпендикулярна плоскости
перпендикулярна плоскости 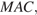 диагонали
диагонали  и
и 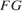 четырёхугольника
четырёхугольника 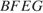 перпендикулярны, следовательно,
перпендикулярны, следовательно,
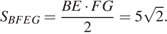
Ответ: 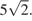
54. C 2 № 501416. Длины ребер BC, BB 1 и BA прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 равны соответственно 8, 12 и 9. Найдите расстояние от вершины D 1 до прямой A 1C.
Решение.
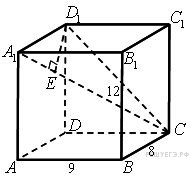 Опустим из точки
Опустим из точки 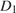 перпендикуляр
перпендикуляр 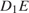 на прямую
на прямую 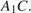 Так как
Так как 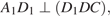 то
то 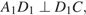 а, значит, отрезок
а, значит, отрезок 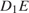 ― высота прямоугольного треугольника
― высота прямоугольного треугольника 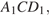 откуда
откуда 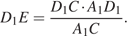 Далее находим:
Далее находим:

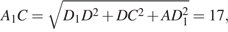
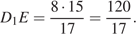
Ответ: 
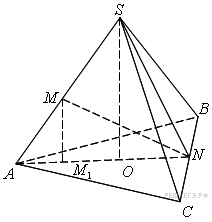
55. C 2 № 484559. В правильной треугольной пирамиде 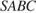 с основанием
с основанием 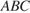 известны ребра
известны ребра 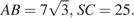 Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер
Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер 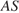 и
и 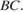
Решение.
Пусть 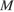 и
и 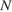 — середины ребер
— середины ребер 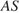 и
и 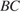 соответственно.
соответственно. 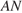 — медиана правильного треугольника
— медиана правильного треугольника  следовательно, находится по формуле
следовательно, находится по формуле  Прямая
Прямая 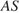 проецируется на плоскость основания и прямую
проецируется на плоскость основания и прямую 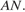 Поэтому проекция точки
Поэтому проекция точки 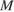 — точка
— точка 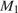 — лежит на отрезке
— лежит на отрезке 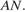 Значит, прямая
Значит, прямая 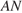 является проекцией прямой
является проекцией прямой 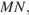 следовательно, угол
следовательно, угол 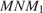 — искомый.
— искомый.
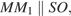 где
где  — центр основания, значит,
— центр основания, значит, 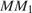 — средняя линия треугольника
— средняя линия треугольника 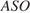 поэтому
поэтому 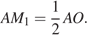 Тогда
Тогда  и
и 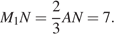 Из прямоугольного треугольника
Из прямоугольного треугольника 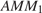 находим:
находим:
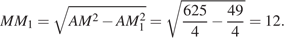
Из прямоугольного треугольника 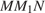 находим:
находим:
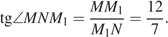
Значит, искомый угол равен 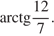
Ответ: 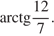
56. C 2 № 500408. Точка 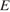 — середина ребра
— середина ребра 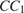 куба
куба 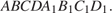 Найдите угол между прямыми
Найдите угол между прямыми  и
и 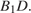
Решение.
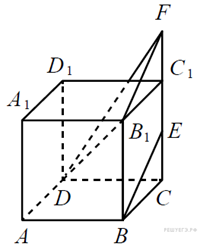 Примем ребро куба за
Примем ребро куба за 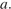 Тогда
Тогда  Проведём через точку
Проведём через точку 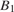 прямую, параллельную
прямую, параллельную 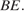 Она пересекает продолжение ребра
Она пересекает продолжение ребра 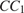 в точке
в точке 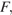 причём
причём  Искомый угол равен углу
Искомый угол равен углу 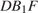 (или смежному с ним).
(или смежному с ним).
В прямоугольном треугольнике  с прямым углом
с прямым углом 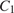
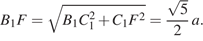
В прямоугольном треугольнике 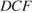 с прямым углом
с прямым углом 

В треугольнике 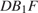 по теореме косинусов
по теореме косинусов
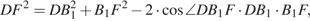
откуда 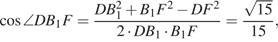 а тогда
а тогда 
Ответ: 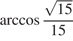 .
.
Примечание.
Ответ может быть представлен и в другом виде:
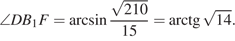
57. C 2 № 501985. В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 6, а боковые рёбра равны 12. Найдите площадь сечения пирамиды плоскостью, проходящей через точку C и середину ребра MA параллельно прямой BD.
Решение.
Пусть точка 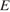 — середина ребра
— середина ребра 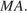 Отрезок
Отрезок 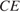 пересекает плоскость
пересекает плоскость 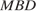 в точке
в точке 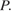 В треугольнике
В треугольнике 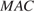 точка
точка 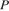 является точкой пересечения медиан, следовательно,
является точкой пересечения медиан, следовательно,  где
где  — центр основания пирамиды. Отрезок
— центр основания пирамиды. Отрезок 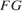 параллелен
параллелен 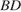 и проходит через точку
и проходит через точку 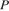 (точка
(точка 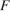 принадлежит ребру
принадлежит ребру 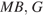 —ребру
—ребру 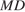 ), откуда
), откуда

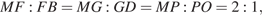
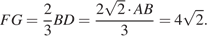
Четырёхугольник 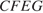 — искомое сечение. Отрезок
— искомое сечение. Отрезок 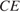 — медиана треугольника
— медиана треугольника 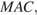 значит,
значит,
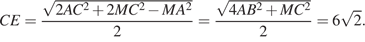
Поскольку прямая 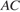 перпендикулярна плоскости
перпендикулярна плоскости 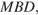 диагонали
диагонали 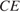 и
и 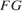 четырёхугольника
четырёхугольника 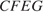 перпендикулярны, следовательно,
перпендикулярны, следовательно,
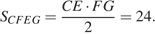
Ответ: 24.
58. C 2 № 500816. Сторона основания правильной треугольной призмы  равна
равна 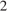 , а диагональ боковой грани равна
, а диагональ боковой грани равна  Найдите угол между плоскостью
Найдите угол между плоскостью 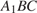 и плоскостью основания призмы.
и плоскостью основания призмы.
Решение.
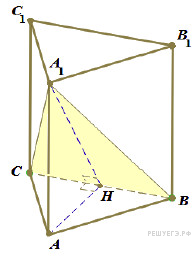 Обозначим
Обозначим 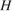 середину ребра
середину ребра  Так как треугольник
Так как треугольник 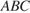 равносторонний, а треугольник
равносторонний, а треугольник 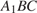 — равнобедренный, отрезки
— равнобедренный, отрезки 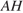 и
и 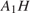 перпендикулярны
перпендикулярны 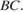 Следовательно,
Следовательно, 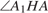 — линейный угол двугранного угла с гранями
— линейный угол двугранного угла с гранями 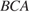 и
и 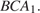 Из треугольника
Из треугольника 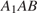 найдем
найдем 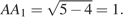 Из треугольника
Из треугольника 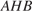 найдем
найдем 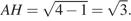
Из треугольника 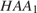 найдем:
найдем: 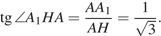
Искомый угол равен 
Ответ: 
59. C 2 № 484576. В правильной шестиугольной призме 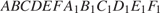 стороны основания которой равны 4, а боковые ребра равны 3, найдите расстояние от точки В до прямой
стороны основания которой равны 4, а боковые ребра равны 3, найдите расстояние от точки В до прямой 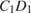 .
.
Решение.
Так как ABCDEF правильный шестиугольник, то прямые BE и CD параллельны, параллельны также прямые 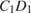 и
и 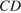 , следовательно, прямые
, следовательно, прямые 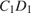 и
и  параллельны. Расстояние от точки B до прямой
параллельны. Расстояние от точки B до прямой 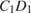 , равно расстоянию между прямыми
, равно расстоянию между прямыми 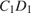 и
и  .
.
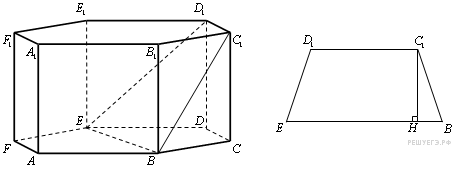
В трапеции 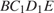 :
:
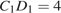 ,
, 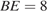 ,
, 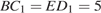 ,
,  ,
,
тогда
 .
.
Ответ:  .
.
60. C 2 № 505237. Косинус угла между боковой гранью и основанием правильной треугольной пирамиды равен 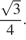 Найдите угол между боковыми гранями этой пирамиды.
Найдите угол между боковыми гранями этой пирамиды.
Решение.
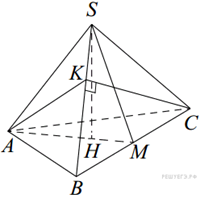 Пусть
Пусть 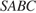 — данная пирамида с вершиной
— данная пирамида с вершиной 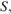
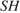 — ее высота,
— ее высота, 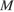 — середина
— середина 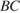 ,
, 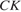 — высота треугольника
— высота треугольника 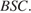 Угол
Угол 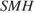 — угол между боковой гранью пирамиды и основанием.
— угол между боковой гранью пирамиды и основанием.
Пусть  тогда
тогда
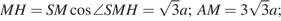
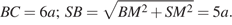
Найдем площадь треугольника 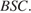 двумя способами:
двумя способами: 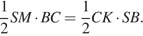 Значит,
Значит, 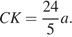
Ребро 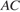 перпендикулярно плоскости
перпендикулярно плоскости 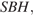 поэтому
поэтому 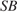 и
и 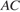 перпендикулярны, следовательно, плоскость
перпендикулярны, следовательно, плоскость 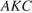 перпендикулярна ребру
перпендикулярна ребру 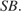 Искомый угол между боковыми гранями равен углу при вершине равнобедренного треугольника
Искомый угол между боковыми гранями равен углу при вершине равнобедренного треугольника 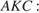
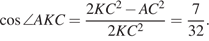
Ответ: 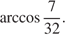
Дата публикования: 2014-10-20; Прочитано: 3167 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
