Производящие функции

В комбинаторных задачах на подсчет числа объектов при наличии некоторых ограничений искомым решением часто является последовательность вида

a₀, a₁, a₂, …, a_k, …, (4)

где a_k (k=0, 1 …) – число искомых объектов «размерности» k. Например, если мы ищем число подмножеств n-элементного множества, то Удобным представлением этой последовательности является формальный ряд

(5)

=

Замечание. Фраза «формальный ряд» означает, что (5) рассматривается просто как вид (или форма) записи последовательности (4), и никакой другой смысл в эту запись не вкладывается.

Определение. Формальный ряд (5) называется производящей функцией последовательности (4).

Производящие функции получили широкое распространение в комбинаторике в силу следующих обстоятельств.

Во-первых, они позволяют, не вычисляя каждое из чисел
a₀, a₁, a₂, …., a_k, … по отдельности, получить все эти решения в «собирательной» форме. В то же время для любого фиксированного k (k = 0, 1, …) число может быть вычислено аналитическими методами. Действительно, из курса математического анализа известно, что при выполнении определенных требований функция f(x) может быть разложена в ряд Маклорена (частный случай ряда Тейлора, соответствующий разложению в окрестности точки 0),

(6)

где а_i = (i=0,1,...).

Сравнение (6) и (5) дает основание считать, что в записи (5) , и трактовать A(x) как значение функции A в точке x.

Во-вторых, производящие функции позволяют в явном виде находить функцию, определяющую последовательность (4), устанавливать соотношения между числами a₀, a₁, a₂, …, a_k, …, а также получать различные тождества. Это достигается с помощью использования ряда стандартных методов, использующих операции, определенные над производящими функциями. Рассмотрим некоторые из таких операций.

Пусть заданы производящие функции

=

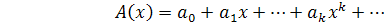и

.

Суммой производящих функций A(x) и B(x) называется производящая функция

A(x)+B(x)=(a₀+b₀)+(a₁+b₁)x+…+(a_k+b_k)x^k+… =

Произведением производящей функции A(x) на число p называется производящая функция

Произведением производящих функций A(x) и B(x) (оно также называется произведением Коши) называется производящая функция

A(x) B(x) = с₀+с₁x+…+с_kx^k+… = ,

где c_k = a₀b_k + a₁b_k-1 +…+ a_k-1b₁ + a_kb₀ = для всех k=0, 1 ….

Производной от производящей функции A(x) называется производящая функция

Пример 15. Найти производящую функцию последовательности, определяемой функцией f(k) = 1 для всех k = 0, 1, ….

Решение: Заданная последовательность имеет вид

1, 1, …, 1, ….

Из (5) следует, что производящая функция A(x)=1+x+x²+…+x^k+….

При | x |<1 правая часть этого равенства представляет собой бесконечно убывающую геометрическую прогрессию. Считая, что условие | x |<1 выполняется и заменяя прогрессию ее суммой, получим, что

.

Пример 16. Найти производящую функцию последовательности, определяемой функцией для всех k = 0, 1, ….(n фиксировано).

Решение. Из (5) следует, что

Пример 17. Доказать тождество

. (*)

Решение: Дифференцируя равенство

получим .

Подставив в это равенство x = 1, получим (*).

2.7. Производящие функции числа основных
комбинаторных объектов

Производящая функция является устройством, отчасти напоминающим мешок. Вместо того чтобы нести отдельно много предметов, что могло бы оказаться затруднительным, мы собираем их вместе, и тогда нам нужно нести лишь один предмет – мешок.

Д. Пойа

Биномиальная теорема указывает на то, что (1+z)ⁿ – это производящая функция для последовательности . Действительно,

Часто бывает удобно вместо ряда (5) рассматривать ряд вида

, (7)

который мы будем называть экспоненциальной производящей функцией последовательности (4).

Производящие функции числа основных комбинаторных объектов:

1) производящая функция для

2) Производящей функцией числа сочетаний из множества

E = {e₁, e₂, …, e_n}, заданных условиями, согласно которым кратность каждого элемента e _i может быть одним из чисел 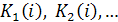является функция

+…),

а коэффициент при x^k , полученный после раскрытия скобок, равен числу таких сочетаний.

3) Найти число сочетаний с повторениями из n элементов по k без всяких ограничений на кратность элементов в данном сочетании (т.е. кратность каждого элемента может быть любым целым неотрицательным числом), таким образом,

В данном случае производящая функция выглядит следующим образом:

.

4) Найти число сочетаний с повторениями из n элементов по k, в которых каждый элемент встречается не менее r раз (т.е. кратность каждого элемента может быть одним из чисел r, r+1, r+2,...). Производящей функцией для числа сочетаний такого вида является функция

.

5)

– экспоненциальная производящая функция числа размещений A_n^k.

6)

– экспоненциальная производящая функция числа n^k (т.е. числа k-пере­становок с повторением элементов в n-элементном множестве).

Пример 18. Какой вид имеет производящая функция для сочетаний из трех элементов, в которых каждый элемент встречается не менее одного раза?

Решение: n = 3, r = 1, тогда

Пример 19. Имеется множество M = {a, b, c}, из элементов которого строятся пятиместные размещения со следующими ограничениями на частоту повторения элементов:

1) элемент a может входить в размещение не более одного раза;

2) элемент b может входить в размещение один или два раза;

3) элемент c может входить в размещение неограниченное число раз.

Найти число размещений описанного типа.

Решение: Как известно, число k-размещений с повторением элементов в n-элементом множестве равняется n^k.

Производящая функция для размещений с повторениями выглядит так:

коэффициент при равен .

Согласно условиям исходной задачи производящая функция выглядит следующим образом:

.

Теперь, перемножив скобки, ищем коэффициент перед , он и есть решение исходной задачи.

Получаем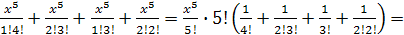

=

=

.

Число размещений равно 65.

Пример 20. Какой вид имеет производящая функция для размещений из трех разных элементов, в которых каждый элемент встречается не менее двух раз?

Решение: Известно, что .