Теория многокритериальной оптимизации по Парето

Открытие и практическое применение линейного программирования было оценено мировой научной общественностью как одно из величайших достижений в области моделирования управленческих решений. За это достижение мирового значения американцу Т.Купмасу и советскому математику-экономисту Л.В.Канторовичу в 1975 г. была присуждена Нобелевская премия по экономике.

Однако, при всех безусловных и качественно новых, ранее недоступных возможностях исследований экономики с помощью линейного программирования оно обладает и рядом недостатков. Один из наиболее важных, часто оказывающий существенное влияние на системный анализ экономических процессов недостаток заключается в том, что оценка качества управления осуществляется по численному значению одной целевой функции. На практике же эту оценку часто приходится проводить одновременно по нескольким показателям. Поясним на примерах.

Хорошо известно, что стремление к максимизации прибыли при многих сделках одновременно сопутствует возрастание риска при этом.

Для опытных менеджеров «золотой серединой» оказывается недобор прибыли по отношению к потенциально возможной при достаточно высокой надежности при принятии решений в части избежать нежелательно рискованных потерь.

Другой хорошо известный пример: стремление к максимизации прибыли при минимальных затратах. Очевидно, что с системных позиций такие противоречивые устремления менеджера просто невозможны, так как прирост прибыли в процессе производства всегда связан с дополнительными производственными (переменными) издержками. Минимизировать издержки можно лишь ничего не производя; тогда издержки минимальны, но и прибыль равна нулю. Можно, однако, поставить задачу производства заданного объема продукции при минимальных затратах. Это вполне реальная постановка, но получается однокритериальная задача (минимум затрат).

Итак, на содержательном уровне многокритериальная задача может оказаться противоречивой, т.е. не содержать решения. Но практика такие задачи действительно выдвигает. Следовательно, математика должна искать разумные, адекватные практике, подходы.

Простейшая попытка – записать задачу по аналогии с однокритериальной:

Здесь - желательные критерии оптимальности,

- совокупность в общем виде линейных ограничений,

- вектор искомых переменных.

Все выражения в (3.1) мы устремляем к максимуму, опираясь на известное свойство о том, что если в реальном критерии имеет место стремление к минимуму

то взятие обратного знака дает:

в) xmax= " x Î[0, x 1]

б) xmax=0

f3 (x)

A

x 1

x

f2 (x)

A

x 1

x

f1 (x)

A

x 1

x

а) xmax=x 1 =A

Рис.5.1

Посмотрим на самых простых примерах, к чему может привести постановка (3.1), (3.2). Возьмем одномерный случай и на рисунке изобразим возможные сочетания для трех критериев, полагая, что все критерии устремлены к максимуму (рис.5.1).

Как мы видим из рисунка, математические схемы вполне соответствуют отмеченному выше содержательному смыслу: при одном и том же множестве ограничений оптимальное значение по каждому из трёх критериев f1(x), f2(x), f3(x) будет разным, и это зависит от угла наклона соответствующих прямых f1(x), f2(x), f3(x). При возрастающей целевой функции максимум достигается на правой границе (а), при убывающей целевой функции максимум достигается на левой границе (б), если функция постоянна, то любое допустимое значение x обеспечивает максимум (и минимум) функционала.

Следовательно, многокритериальную задачу нужно решать, не добиваясь максимума или минимума для каждого функционала в отдельности, а построить «комплексную» целевую функцию, включающую частные функционалы: , и для функции искать оптимальное значение xmax. В итоге, мы все равно сводим задачу к однокритериальной, хотя на содержательном уровне она будет отражать многокритериальные тенденции.

Различными авторами рассматривались способы выбора функций . Мы рассмотрим один способ, связанный с именем Парето. Преимущество данного способа, во-первых, в том, что он не «портит» структуру задачи линейного программирования (функционал остается линейным); во-вторых, на формальном уровне хорошо отвечает многим содержательно ясным предпосылкам. Объем вычислений при этом может существенно возрастать, но качественно решаемые дополнительные задачи остаются однотипными, требуя лишь многократного применения на ЭВМ одинакового программного обеспечения. Т.е. повышается только механическая трудоемкость решения задачи при неизменном ее качественном уровне.

Поставим задачу линейного программирования с k-й целевой функцией () в виде:

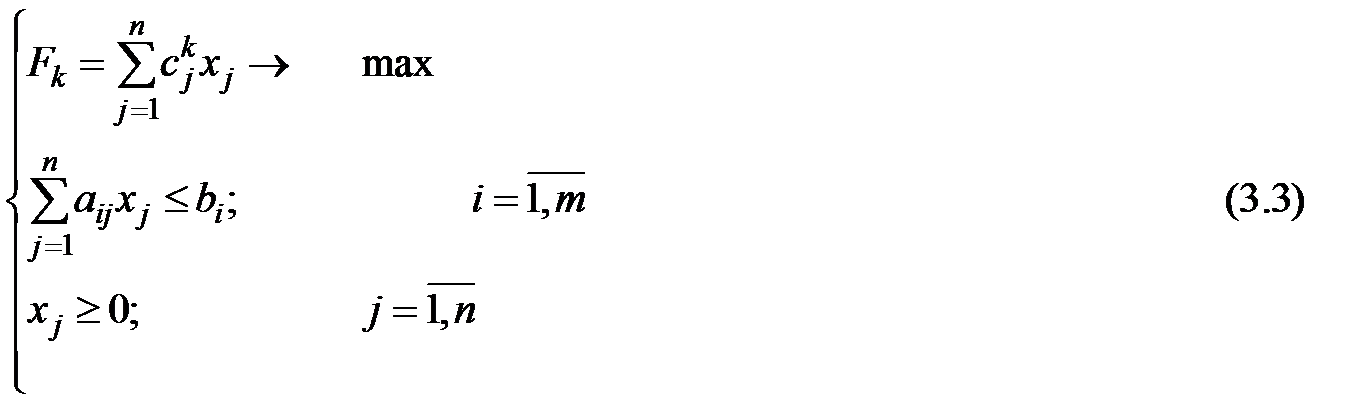
После решения всех задач типа (3.3) будем иметь l оптимальных значений функционалов. Обозначим их через .

Поставим следующую однокритериальную задачу максимизации по Парето и изучим ее свойства:

где и , - соответственно весовые коэффициенты и нормирующие числа для частных критериев :

.

Весовые коэффициенты для частных критериев , как правило, задаются лицом, принимающим решения, экспертным образом и отражают его взгляды на значимость каждого частного критерия.

Оптимальное решение задачи (3.4) при некотором фиксированном наборе весов называют эффективной точкой по Парето. Множество всех эффективных точек при возможных допустимых значениях называют множеством Парето. Это множество обладает свойствами достижения компромиссов при различных весах частных критериев. Покажем, в каком смысле это понимается.

Допустим, что при некотором заданном наборе весовых коэффициентов , и известных значениях функционалов при k-ом частном критерии 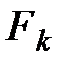, путем решения однокритериальной задачи (3.4) найдена оптимальная эффективная точка 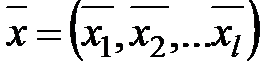и оптимальное значение функционала F.Утверждается, что если есть другая эффективная точка при тех же весах , для которой некоторые значения больше соответствующих значений оптимального эффективного решения, то всегда будет по крайней мере одно значение .

Первый вывод: противостоящим сторонам нельзя достичь компромисса, имея одинаковые веса частных критериев, если одна сторона стремится выиграть по всем частным показателям одновременно. По крайней мере, по одному из них неизбежна уступка.

Допустим противное, т.е. что 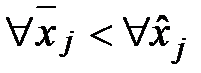. Тогда, согласно (3.4), для всех (поскольку они одинаковы в обоих вариантах) будет и соответственно, .

Так как в функционале (3.4) остальные компоненты для обоих вариантов одинаковы, то окажется, что оптимальной значение будет меньше альтернативной величины , что противоречит исходному утверждению об оптимальности .

Второй вывод: может существовать множество эффективных точек. На содержательном уровне это означает наличие множества условий, выражающихся приоритетами частных интересов, при которых возможно достижение компромисса. Следует понимать, что исходя из произвольных начальных условий, достижение компромисса между конфликтующими сторонами не всегда возможно.

Из практики известны случаи, когда стороны, сев за стол переговоров, ни о чем не смогли договориться. На системном уровне это означает, что процесс переговоров не был сторонами предварительно смоделирован, не было установлено, что множество эффективных точек пусто или не имеет пересечений (т.к. нет точек взаимных интересов и возможности взаимных уступок). Т.е. переговоры не были предварительно подготовлены и начинать их было бесполезно.

Именно это свойство системной организованности и системной подготовленности дает основание включить этот параграф в курс системного анализа.