 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства функции и плотности распределения вероятности
|
|
1) 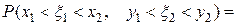
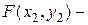
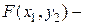
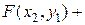
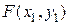 .
.
2) 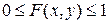 .
.
3) 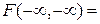

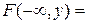 0.
0.
4)  .
.
5) 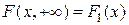 ,
, 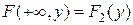 , где
, где 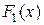 и
и 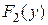 – функции распределения вероятности случайных величин
– функции распределения вероятности случайных величин 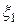 и
и 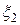 .
.
6) В любой точке непрерывности функции 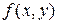 ,
, 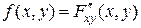 .
.
7) 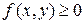 .
.
8) 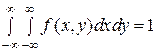 .
.
9) 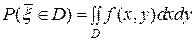 .
.
10)  ,
, 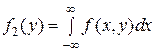 ,
,
где  и
и  – плотности распределения случайных величин
– плотности распределения случайных величин 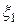 и
и 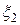 .
.
Условной плотностью распределения случайной величины 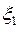 при условии, что
при условии, что 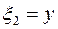 называют функцию
называют функцию 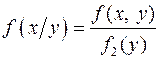 ,
, 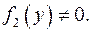
Аналогично определяют 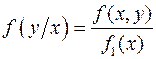 ,
, 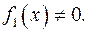
Равенство 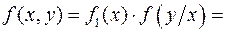
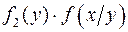 называют теоремой умножения плотностей вероятности.
называют теоремой умножения плотностей вероятности.
Случайные величины 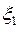 и
и 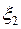 называются независимыми, если для любых чисел
называются независимыми, если для любых чисел  ,
,  случайные события
случайные события 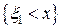 и
и 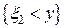 независимы (см. стр.12).
независимы (см. стр.12).
Случайные величины независимы, если выполняется любое из условий:

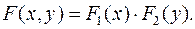

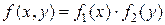 .
.

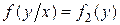 или
или 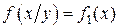 .
.
Для двумерных случайных величин вводят понятия начальных и центральных моментов, из которых наиболее часто используются математические ожидания  ,
, 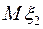 и дисперсии
и дисперсии  ,
, 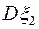 составляющих, а также условные математические ожидания и корреляционный момент.
составляющих, а также условные математические ожидания и корреляционный момент.
Условным математическим ожиданием для дискретного случайного вектора называется сумма:
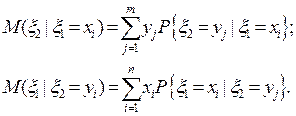
Для двумерных непрерывных случайных величин условным математическим ожиданием называется интеграл:
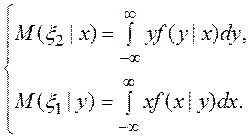
Величина 
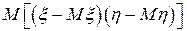 называется корреляционным моментом (ковариацией ) двух случайных величин
называется корреляционным моментом (ковариацией ) двух случайных величин 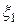 и
и 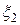 .
.
Если  – непрерывная двумерная случайная величина с плотностью распределения
– непрерывная двумерная случайная величина с плотностью распределения 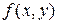 , то
, то
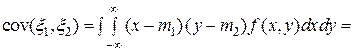

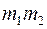 ,
,
где 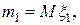
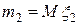 .
.
Для дискретного случайного вектора
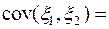
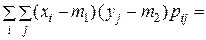
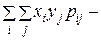
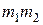 .
.
Величина 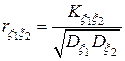 называется коэффициентом корреляции случайных величин
называется коэффициентом корреляции случайных величин 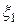 и
и 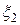 .
.
Если 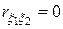 , то случайные величины
, то случайные величины 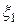 и
и 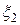 называются некоррелированными.
называются некоррелированными.
Дата публикования: 2014-10-20; Прочитано: 586 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
