 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Алгоритм решения уравнений третьей степени в радикалах
|
|
1. Уравнение третьей степени 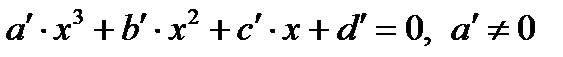 делением обеих частей на
делением обеих частей на 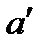 приводим к равносильному уравнению
приводим к равносильному уравнению 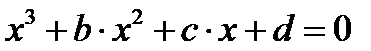 .
.
2. Заменой  приводим к уравнению
приводим к уравнению 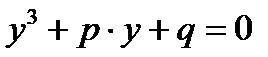 .
.
3. Вычисляем 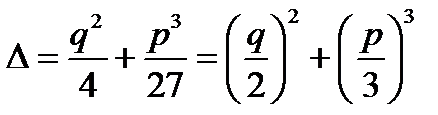 - дискриминант кубического уравнения.
- дискриминант кубического уравнения.
4. Находим один из корней уравнения 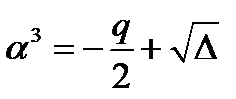 , вообще говоря, с комплексными коэффициентами (если
, вообще говоря, с комплексными коэффициентами (если 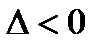 , то берём любой комплексный квадратный корень из
, то берём любой комплексный квадратный корень из  ), и число
), и число 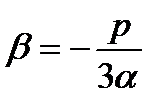 . При этом, если
. При этом, если 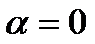 , то и
, то и 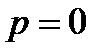 , и в пункте 2 уравнение принимает вид
, и в пункте 2 уравнение принимает вид 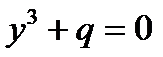 , решение которого очевидно.
, решение которого очевидно.
5. Если 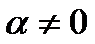 , то находим корни уравнения
, то находим корни уравнения 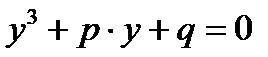 :
:  , где
, где 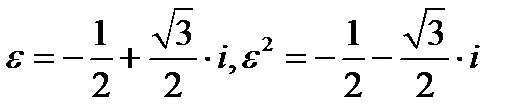 - комплексные недействительные корни кубические из единицы.
- комплексные недействительные корни кубические из единицы.
6. Находим корни исходного уравнения  .
.
Теорема 4.2. (О множестве всех решений кубического уравнения с действительными коэффициентами). Пусть 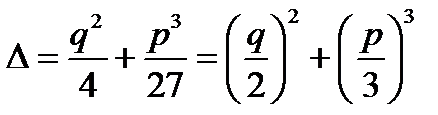 - дискриминант кубического уравнения (1)
- дискриминант кубического уравнения (1) 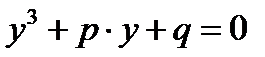 . Тогда
. Тогда
1) если  , то уравнение (1) имеет один действительный и два недействительных комплексных сопряжённых корня;
, то уравнение (1) имеет один действительный и два недействительных комплексных сопряжённых корня;
2) если 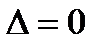 , то все три корня уравнения (1) действительные и хотя бы два из них совпадают;
, то все три корня уравнения (1) действительные и хотя бы два из них совпадают;
3) если  , то все три корня уравнения (1) действительные и различные.
, то все три корня уравнения (1) действительные и различные.
Пример 15. Решить уравнение 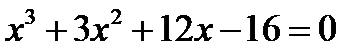 методом Кардано.
методом Кардано.
Так как исходное уравнение является приведённым, то сразу делаем замену  :
: 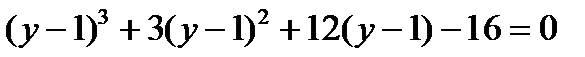
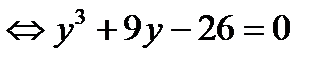 .
.
Итак, 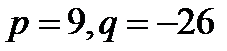 . Тогда
. Тогда  . Значит, по теореме 4.2 уравнение имеет один действительный и два недействительных комплексных сопряжённых корня. Находим один из корней уравнения
. Значит, по теореме 4.2 уравнение имеет один действительный и два недействительных комплексных сопряжённых корня. Находим один из корней уравнения 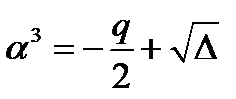 или
или 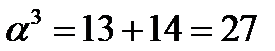 . Возьмём
. Возьмём 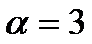 . Тогда
. Тогда  . Поэтому
. Поэтому 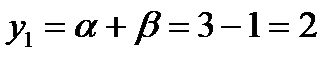 ,
, 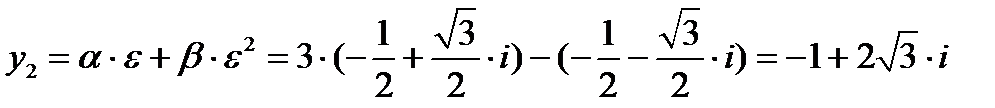 ,
, 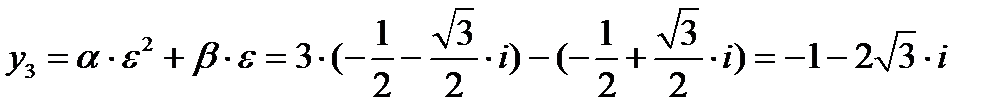 .
.
Находим корни исходного уравнения по формулам: 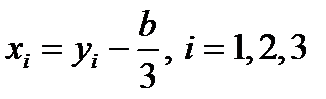 . Итак,
. Итак, 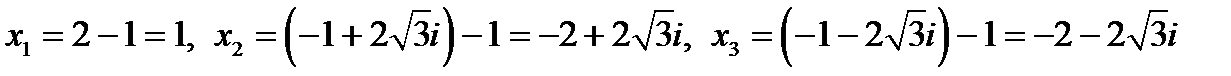 .
.
Дата публикования: 2014-10-20; Прочитано: 1090 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
