Логические алгоритмы

Логическими принято называть алгоритмы, которые содержат предписания (операции) относительно объектов нечисловой природы. Характерной особенностью логических алгоритмов является выбор на каждом шаге по определенным правилам альтернативной операции, осуществляемой при переходе к следующему шагу. К логическим задачам относят многие игры. Однако выделение логических задач из множества математических задач достаточно условно – в большинстве случаев задачи являются смешанными: в них присутствуют и числовые, и логические операции. Так, машинные алгоритмы игры в шахматы используют на каждом шаге вычисление значения некоторой функции, учитывающей оценку позиции после каждого следующего хода (точнее, полухода) и стоимость размена фигур.

1.3.1. Задача "Поиск пути в лабиринте"

Эта задача восходит к греческой мифологии, в которой Тезею, оказавшемуся в лабиринте, где обитал Минотавр, необходимо было выбраться из лабиринта. Решить данную задачу ему помогла Ариадна (А), дав ему клубок ниток, один конец которых держала она сама. По мере углубления Тезея в лабиринт клубок разматывался; наматывая потом нитки, Тезей благополучно вернулся к выходу.

Рассмотрим задачу поиска пути в лабиринте в общем случае.

Представим лабиринт в виде конечной системы площадок, от которых расходятся коридоры, причём каждый коридор соединяет две площадки (будем называть их смежными);возможно существование таких площадок, из которых можно пройти только в один коридор (такие площадки будем называть тупиками). Геометрически лабиринт можно представить в виде системы точек А, В, С,..., изображающих площадки, и совокупности отрезков АВ, ВС,..., изображающих коридоры, которые соединяют определённые пары данных точек (рис. 1.16). Смежными являются, например, площадки В и С, К и М и т. д., а тупиковыми – площадки A, D, I, J.

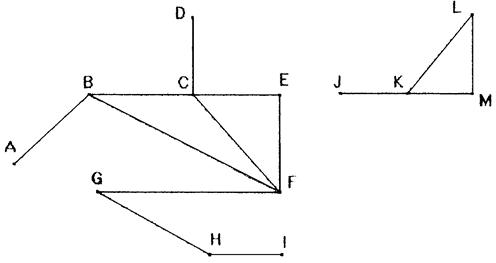
Рис. 1.16. Геометрическое представление лабиринта

Будем говорить, что площадка Y достижима из площадки X, если существует путь от X к Y через промежуточные коридоры и площадки. Точнее: либо X и Y - смежные площадки, либо существует последовательность площадок Х1, Х2,..., Хn таких, что X и Х1, Х1 и Х2..., и т.д., и, наконец, Хn и Y являются смежными. Отметим, что если Y достижима из X, то она достижима и посредством простого пути, т.е. такого пути, в котором каждая площадка (а тем более и каждый коридор) проходится лишь один раз. Например, путь ABCD является простым, а путь ABCFECD – нет.

Поскольку заранее устройство лабиринта неизвестно, решение задачи должно быть представлено в виде общего метода поиска для любого лабиринта и при любом расположении площадок Х и Y, где Х – начальная площадка, а Y – конечная, т. е. требуется построить алгоритм поиска пути в лабиринте.

Данная задача решается путем последовательного перебора всех возможных путей ведущих из начальной точки Х в конечную Y. При этом путь ведущий в тупик отмечается как тупиковый, а путь, в результате которого происходит возврат в одну из пройденных точек помечается как замкнутый или циклический. Пройдя таким образом все возможные пути, размеченные как тупиковые, замкнутые и пройденные один или более раз, но не ведущие в тупик или в уже пройденную вершину, производится анализ, на основе которого выбирается кратчайший путь ведущий от входа в лабиринт к его выходу, т.е. от Х к Y.

Если рассматривать вершины лабиринта как вершины графа, а связывающие их коридоры как дуги этого графа, то решения данной задачи можно применить один из методов теории графов о нахождении кратчайших путей между двумя вершинами. Например, волновой алгоритм поиска кратчайшего пути в графе (рассмотрим далее на практиках).

1.3.2. Задача "Ханойские башни"

Эта задача формулируется следующим образом. Имеется три стержня, на одном из которых (назовём его занятым) находятся диски разных диаметров, расположенные на стержне в порядке убывания диаметров снизу вверх, второй стержень назовём свободным, а третий – вспомогательным. Требуется, производя одиночные перемещения дисков, переместить всю "стопку" дисков с занятого стержня на свободный, используя вспомогательный стержень; при этом на любом шаге диски должны быть расположены на каждом стержне в порядке убывания их диаметров (рис 1.17).

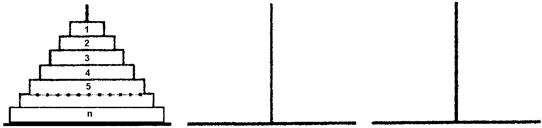
А В С

Рис. 1.17. Ханойские башни

Таблица 1.5

Шаг
А	4-1	4-2	4,3	4,3		4,1	4,1		Æ	Æ		2,1	2,1		Æ	Æ
В	Æ	Æ		2,1	2,1		Æ	Æ		4,1	4,1		4,3	4,3	4-2	4-1
С	Æ			Æ			3,2	3-1	3-1	3,2			Æ		1	Æ

В табл. 1.5 приведен результат решения задачи для случая четырех дисков. Здесь А – занятый в начальный момент (нулевой шаг) стержень, В – свободный, а С – вспомогательный стержень. Цифрами обозначен "номер" диска, причём большему номеру соответствует больший диаметр. Отметим, что в середине процесса решения в качестве вспомогательного выступает то стержень А, то стержень С.

Видно, что процесс перемещения стопки дисков можно разбить на четыре фазы:

1-я фаза – шаги 1-8, в результате которой самый нижний диск оказывается на свободном стержне;

2-я фаза – шаги 9-12; второй по величине диск оказывается на свободном стержне;

3-я фаза – шаги 13 и 14; переносят предпоследний диск на свободный стержень;

и 4-я фаза – шаг 15 – заключительный этап, в результате которого диск с наименьшим диаметром переносится на свободный стержень с уже упорядоченными по убыванию дисками.

То есть, к началу каждой фазы на вспомогательном или занятом стержне собирается стопка дисков, затем в течение данной фазы самый нижний диск стопки перемещается на свободный стержень (в табл. 1.5 номера этих дисков подчёркнуты).

Анализ перемещений дисков позволяет выявить определённые закономерности, составить словесное описание алгоритма перемещений для общего случая, когда количество дисков произвольно, а затем перейти к разработке схемы алгоритма.

В качестве примера решения задачи «Ханойские башни» можно привести следующий НЕ рекурсивный алгоритм. Если обозначить номера стержней не буквами а цифрами «0», «1» и «2», пронумеровать диски от нуля до N-1 (N – кол-во дисков на занятом стержне), то можно использовать следующее соотношение: на i-ом ходе переносится диск номер k со стержня номер ((-1)^N-k*t mod 3) на стержень номер ((-1)^N-k*(t+1) mod 3). Следуя такой последовательности перемещения дисков задача будет решена за 2ⁿ-1 перемещений. При этом для нахождения чисел t и k воспользуемся теоремой: любое натуральное число i единственным образом представимо в виде i=(2t+1)*2^k, где t и k - целые (т.е. как произведение нечетного числа на некоторую степень двойки). Если i – это очередной ход, то соответственно по указанной формуле для него определяются значения целых чисел t и k. В данном, одном уравнении присутствуют два неизвестных. Однако пользуясь тем, что числа t и k обязательно целые и единственные для натурального числа i, нетрудно построить алгоритм для нахождения их значений.

Отметим также, что в зависимости от того четным или нечетным будет количество дисков на занятом стержне, в качестве вспомогательного и свободного будут выступать соответственно либо стержни «1», «2» либо «2», «1», т.е. стопка будет перемещена либо на первый либо на второй диск. Однако, так или иначе стопка N дисков будет перемещена согласно установленным правилам на один из не занятых стержней (либо на первый (B) либо на второй стержень (C)).

Заключение

1. Любой вычислительный процесс может быть представлен композицией следующих его фрагментов: линейный, ветвящийся, циклический.

2. Для организации разветвлений и циклов могут быть использованы различные операторы; выбор того или иного оператора в конкретном случае остаётся за программистом.

3. При организации разветвлений необходимо стремиться минимизировать логическое выражение, описывающее выбор альтернатив.

4. При организации циклов особенно важны два момента: правильное построение начала цикла и его конца. Важно также обеспечить стыковку цикла с остальной частью алгоритма или циклов друг с другом при их вложенности.

5. СА может быть представлена с разной степенью подробности. Так, предопределённый процесс, например блок ввода/вывода, может включать в себя несколько циклов; визуально фрагмент СА, включающий в себя этот блок, будет выглядеть линейным. В действительности линейными могут быть только очень простые алгоритмы или их некоторые фрагменты.

6. СА допускают эквивалентные преобразования, что может быть использовано для повышения эффективности алгоритмов. Например, имеет смысл выносить, если это возможно, из тела цикла все операторы, не связанные с параметром данного цикла.