 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема о достаточности четырех функций
|
|
Из любой полной в Р 2 системы функций можно выделить полную подсистему, состоящую не более чем из четырех функций.
Доказательство. Пусть { f 0, f 1, fL, fM, fS } – полная система функций, тогда она не лежит целиком ни в одном из классов T 0, T 1, L, M, S. Следовательно, в системе есть функции f 0Ï T 0, f 1Ï T 1, fL Ï L, fS Ï S и fm Ï M. Система { f 0, f 1, fL, fM, fS } Í P 2 и образует полную систему в Р 2. Рассмотрим функцию f 0: f 0(0,..., 0) = 1.
Если f 0(1,..., 1) = 0, то f 0Ï T 1 и f 0Ï M, тогда { f 0, fS, f L} – полная система из трех функций.
Если f 0(1,..., 1) = 1, то f 0Ï S и { f 0, f 1, fL, fM } образует полную систему из четырех функций.
Пример 1, приведенный выше, показывает, что цифру 4 в общем случае уменьшить нельзя, из полной системы { x 1 x 2,0,1, x 1Å x 2Å x 3} нельзя выделить полную подсистему.
Следствие. Базис в Р 2 может состоять максимум из четырех функций.
2.5. Математические теоремы, их виды и логическая структура.
2.5.1. Теоремы прямая, обратная, противоположная.
Простейшая форма математической теоремы такова: " х Î Х (А (х)Þ В (х)) (дальше это утверждение будем называть прямой теоремой). Смысл этой записи: если элемент х множества Х имеет свойство А (х) (условие теоремы), то он имеет и свойство В (х) (заключение теоремы). Пусть, для примера, П ={ Р 1, Р 2, Р 3, …}- множество точек плоскости. Тогда формулировка теоремы Пифагора будет такова:
{"(Р 1Î П, Р 2Î П, Р 3Î П) Ð Р 1 Р 2 Р 3=p/2 Þ | Р 1 Р 2| 2+| Р 2 Р 3| 2=| Р 1 Р 3| 2}.
Исходя из утверждения " х Î Х (А (х)Þ В (х)) можно построить новые утверждения:
" х Î Х (В (х)Þ А (х)) (обратная теорема);
" х Î Х (ù А (х)Þ ù В (х)) (противоположная теорема);
" х Î Х (ù В (х)Þ ù А (х)) (теорема, противоположная обратной).
Сформулируем эти утверждения для теоремы Пифагора:
обратная теорема: {"(Р1 Î П, Р2 Î П, Р3 Î П) | Р1Р2 |2+| Р2Р3 |2=| Р1Р3 |2 Þ Ð Р1Р2Р3 =p/2} (если квадрат какой-либо стороны треугольника равен сумме квадратов остальных сторон, то угол, противолежащий этой стороне - прямой) - верное утверждение;
противоположная теорема: {"(Р1 Î П, Р2 Î П, Р3 Î П) Ð Р1Р2Р3 ¹p/2 Þ | Р1Р2 |2+| Р2Р3 |2¹| Р1Р3 |2} (если какой-либо угол треугольника не прямой,то квадрат противолежащей стороны не может быть равен сумме квадратов остальных сторон - верное утверждение (следствие теоремы косинусов));
теорема, противоположная обратной: {"(Р1 Î П, Р2 Î П, Р3 Î П) | Р1Р2 |2+| Р2Р3 |2¹| Р1Р3 |2 Þ Ð Р1Р2Р3 ¹p/2} (если квадрат какой-либо стороны треугольника не равен сумме квадратов остальных сторон, то угол, противолежащий этой стороне, не может быть прямым) - верное утверждение.
Однако если верна прямая теорема, это не означает, что всегда будут верны все остальные. Рассмотрим утверждение: "если десятичная запись натурального числа заканчивается нулем, то это число делится на пять без остатка"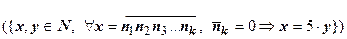 
. Обратная теорема ("если натуральное число делится на пять без остатка, то десятичная запись этого числа заканчивается нулем") 
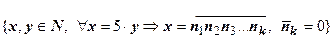- ложна (число х =15 делится нацело на 5, но не оканчивается нулём). Противоположное утверждение "если десятичная запись натурального числа не заканчивается нулем, то это число не делится на пять без остатка" (
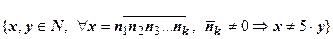) тоже ложно (опровергающий пример - х =15). Утверждение, противоположное обратному: "если натуральное число не делится на пять без остатка, то десятичная запись этого числа не может заканчиваться нулем" 
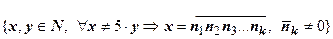- истинно. Докажем общее утверждение
Теор. 2.3.1. Теоремы прямая и противоположная обратной, обратная и противоположная попарно либо обе истинны, либо обе ложны.
Док-во. Составим таблицу истинности для высказываний А, В и требуемых импликаций:
| А | В | ù А | ù В | А Þ В | ù В Þù А | В Þ А | ù А Þù В | Эта таблица является, по существу, подмножеством таблицы Свойства логических операций раздела 2.1. Высказывания и действия над ними. Из неё следуют |
эквивалентности (А Þ В)Û(ù В Þù А); (В Þ А) Û(ù А Þù В), которые и требовалось доказать.
2.5.2. Достаточность и необходимость; существование и единственность.
Переведём формулировку теоремы " х Î Х (А (х)Þ В (х)) на термины "необходимо", "достаточно": если для элемента х множества Х истинно утверждение А (х), то истинно и утверждение В (х). Таким образом, свойство В (х) необходимо для выполнения А (х) (если ложно В (х), то не может быть истинно А (х); необходимо целое число делится на 5 без остатка, если его десятичная запись оканчивается нулём). С другой стороны, условие А (х) достаточно для того, чтобы имело место В (х) (равенство последней цифры десятичной записи целого числа нулю достаточно, чтобы это число делилось на 5 без остатка).
В математике часто встречаются теоремы, для которых утверждения А (х) и В (х) имеют совпадающие области истинности и эквивалентны на этих областях: " х Î Х (А (х)Û В (х) ("для истинности А (х) необходима и достаточна истинность В (х)"; " А (х) истинно тогда и только тогда, когда истиино В (х)"). Как следует из формулы 12. (А Û В) Û (А Þ В)Ù(В Þ А) таблицы "Свойства логических операций", в этом случае одновременно должны быть справедливы и прямая, и обратная теоремы ("треугольник прямоугольный тогда и только тогда, когда квадрат какой-либо стороны равен сумме квадратов остальных сторон"). Закономерен вопрос: зачем вводить два свойства (термина, определения) для описания одной и той же сущности? Ответ заключён в приведённом примере: каждое из свойств может лучше описывать ту или иную сторону этой сущности (одно свойство относится к углам, другое - к сторонам).
Особый класс математических теорем образуют теоремы существования. Их структура - $ х Î ХА (х) (на множестве Х существует элемент х, для которого верно утверждение А (х)). Пример: если непрерывная на отрезке [ a, b ] функция f (x) принимает на концах отрезка значения разных знаков, то на [ a, b ] существует (хотя бы один) корень уравнения f (x)=0 (приведённая на иллюстрации функция имеет три корня). В некоторых случаях принципиальна единственность такого элемента х. Так, при численном решении уравнения f (x)=0 многие итерационные процессы перестают работать, если на [ a, b ] имеется более одного корня уравнения. Существование единственного корня обеспечит такая формулировка теоремы: "если непрерывная на отрезке [ a, b ] функция f (x) монотонна и принимает на концах отрезка значения разных знаков, то на [ a, b ] существует единственный корень уравнения f (x)=0".
Структура теорем существования и единственности: $! х Î ХА (х).
2.5.3. Доказательство от противного; метод математической индукции.
Здесь мы рассмотрит два часто применяющихся метода доказательства теорем: доказательство от противного и метод математической индукции.
2.5.3.1. Доказательство от противного основано на доказанной нами эквивалентности (А Þ В)Û(ù В Þù А) (эквивалентны теоремы прямая и противоположная обратной). Пример - известное доказательство того факта, что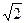 
не может быть рациональным числом (предположим, что 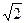= p / q, где p / q - несократимая дробьÞ p 2=2 q 2Þ p - чётно, p= 2 т Þ 4 m 2=2 q 2Þ
Þ q 2=2 m 2Þ q - чётно - противоречие с предположением о несократимости дроби). Таким образом, для доказательства " х Î Х (А (х)Þ В (х)) мы предполагаем, что истинно утверждение ù В, доказываем " х Î Х (ù В (х)Þù А (х)), и противоречие между А (х) и ù А (х) приводит к выводу ù ù В = В.
2.5.3.2. Метод математической индукции часто применяется, если Х = N (или Х - бесконечное подмножество множества N). Доказательство утверждения " n Î N (А (n)Þ В (n)) проводится в два этапа: 1. Доказывается утверждение А (1); 2. Доказывается " n ³1 А (n)Þ А (n +1).
2.6. Формальная аксиоматическая теория.
2.6.1. Основные определения.
Формальная система (формальная теория, аксиоматическая теория) — результат строгой формализации теории, предполагающей полную абстракцию от смысла слов используемого языка, причем все условия, регулирующие употребление этих слов в теории, явно высказаны посредством аксиом и правил, позволяющих вывести одну фразу из других.
Формальная система — это совокупность абстрактных объектов, не связанных с внешним миром, в которой представлены правила оперирования множеством символов в строго синтаксической трактовке без учёта смыслового содержания, то есть семантики.
Многие научные теории (не обязательно математические) строятся по следующему принципу. Сначала предлагаются некоторые основные понятия и некоторые исходные законы (аксиомы), присущие основным понятиям. Далее формулируются производные понятия и по определенным правилам доказываются некоторые утверждения (теоремы), относящиеся к основным и производным понятиям. Совокупность основных и производных понятий, аксиом и теорем, построенная таким способом, называется аксиоматической системой.
Часто аксиомы (а значит, и теоремы) аксиоматической системы сохраняют истинность при замене одних основных понятий другими (как, например, в теории колебаний, которая находит применение в механике, электронике, оптике). Это позволяет рассматривать аксиоматические системы с двух позиций: синтаксически (принципы построения правильных и истинных предложений) и семантически (связь смысла правильных и истинных предложений со смыслом основных понятий).
Для исследования синтаксиса аксиоматической системы требуется ее полная формализация, т.е. символическое представление основных и производных понятий, аксиом, правил вывода и теорем. Поэтому формальная аксиоматическая теория (формальная система) - это синтаксический аспект (сторона) аксиоматической системы. Точное же определение понятия формальной аксиоматической теории включает следующие компоненты.
Во-первых, каждая формальная аксиоматическая теория должна иметь свой формальный язык. Формальный язык считается полностью определенным, когда задано (счётное) множество его символов и описаны формулы языка. Любая конечная последовательность символов языка называется выражением этого языка. Среди всех возможных выражений выделяются формулы языка, под которыми подразумеваются правильно построенные, утверждающие нечто осмысленное предложения языка.
Во-вторых, каждая формальная аксиоматическая теория должна иметь свою систему аксиом - подмножество заведомо истинных формул, из которых по правилам теории могут быть выведены все истинные предложения этой теории (обычно к системе аксиом предъявляются требования непротиворечивости, независимости и полноты, среди которых обязательным является лишь требование непротиворечивости).
В-третьих, каждая формальная аксиоматическая теория должна располагать конечным множеством правил вывода. Каждое правило вывода содержит формулы-посылки и формулу-заключение, выводимую при определенных этим правилом условиях из формул-посылок. Формула-заключение называется непосредственным следствием формул-посылок по данному правилу вывода.
Доказательством в формальной аксиоматической теории называется всякая последовательность формул, в которой каждая формула есть либо аксиома теории, либо непосредственное следствие каких-либо предыдущих формул этой последовательности по одному из правил вывода данной теории. Формула А называется теоремой теории (обозначается ├ А) тогда и только тогда, когда существует доказательство, в котором А является заключительной формулой.
Выводом из множества гипотез (посылок) Г в формальной аксиоматической теории называется всякая последовательность формул, в которой каждая формула есть либо аксиома теории, либо гипотеза из множества Г, либо непосредственное следствие каких-либо предыдущих формул этой последовательности по одному из правил вывода данной теории. Формула А называется следствием множества гипотез Г (обозначается Г ├ А) тогда и только тогда, когда существует вывод из множества гипотез Г, в котором А является заключительной формулой.
Т.О. Формальная теория считается определенной, если:
- Задано конечное или счётное множество произвольных символов. Конечные последовательности символов называются выражениями теории.
- Имеется подмножество выражений, называемых формулами.
- Выделено подмножество формул, называемых аксиомами.
- Имеется конечное множество отношений между формулами, называемых правилами вывода.
Обычно имеется эффективная процедура, позволяющая по данному выражению определить, является ли оно формулой. Часто множество формул задаётся индуктивным определением. Как правило, это множество бесконечно. Множество символов и множество формул в совокупности определяют язык или сигнатуру формальной теории.
Чаще всего имеется возможность эффективно выяснять, является ли данная формула аксиомой; в таком случае теория называется эффективно аксиоматизированной или аксиоматической. Множество аксиом может быть конечным или бесконечным. Если число аксиом конечно, то теория называется конечно аксиоматизируемой. Если множество аксиом бесконечно, то, как правило, оно задаётся с помощью конечного числа схем аксиом и правил порождения конкретных аксиом из схемы аксиом. Обычно аксиомы делятся на два вида: логические аксиомы (общие для целого класса формальных теорий) и нелогические или собственные аксиомы (определяющие специфику и содержание конкретной теории).
Для каждого правила вывода R и для каждой формулы A эффективно решается вопрос о том, находится ли выбранный набор формул в отношении R с формулой A, и если да, то A называется непосредственным следствием данных формул по правилу R.
Выводом называется всякая последовательность формул такая, что всякая формула последовательности есть либо аксиома, либо непосредственное следствие каких-либо предыдущих формул по одному из правил вывода.
Формула называется теоремой, если существует вывод, в котором эта формула является последней.
Теория, для которой существует эффективный алгоритм, позволяющий узнавать по данной формуле, существует ли ее вывод, называется разрешимой; в противном случае теория называется неразрешимой.
Теория, в которой не все формулы являются теоремами, называется абсолютно непротиворечивой.
2.6.2. Определение и разновидности дедуктивных теорий.
Дедуктивная теория считается заданной, если:
Дата публикования: 2014-10-20; Прочитано: 1135 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
