 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Дифференциалданатын функциялар туралы теоремалар
|
|
Анықтама 1. 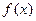 функциясы х=с нүктесінде локальді максимумге (минимумге) жетеді деп айтамыз, егер
функциясы х=с нүктесінде локальді максимумге (минимумге) жетеді деп айтамыз, егер 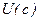 аймағы табылып, төмендегі теңдік орындалса:
аймағы табылып, төмендегі теңдік орындалса:
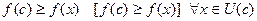
Локальді максимум (max) және минимум (min) функцияның экстремумдары деп аталады.
Теорема 1. (Ферма). Егер 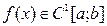 болып және
болып және 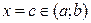 нүктесінде экстремумы бар болса, онда
нүктесінде экстремумы бар болса, онда
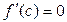 (1)
(1)
Дәлелдеуі. 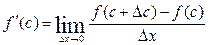 (2)
(2)
c нүктесі максимум нүктесі болсын. Онда ең кіші 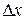 үшін
үшін 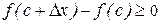 . (2)-ден
. (2)-ден 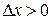 үшін
үшін 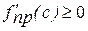 , ал
, ал 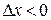 үшін
үшін 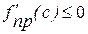 . Бұдан,
. Бұдан, 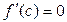 .
.
Ферма теоремасының геометриялық мағынасы:  функциясының экстремум нүктесінде жүргізілген жанама
функциясының экстремум нүктесінде жүргізілген жанама  осіне параллель.
осіне параллель.
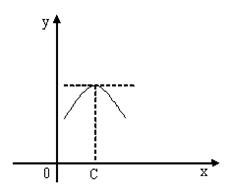
Сурет 14
Бұл 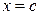 нүктесінде экстремум болуының қажетті шарты, бірақ жеткілікті шарты емес.
нүктесінде экстремум болуының қажетті шарты, бірақ жеткілікті шарты емес. 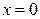 нүктесі
нүктесі 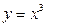 функциясының (мысал 1б, лекция 7) экстремумы болмайды,
функциясының (мысал 1б, лекция 7) экстремумы болмайды, 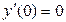 теңдігі орындалса да. Сонымен қатар, экстремум туындысы табылмайтын нүкте болуы да мүмкін,
теңдігі орындалса да. Сонымен қатар, экстремум туындысы табылмайтын нүкте болуы да мүмкін, 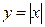 функциясында (мысал 1в, лекция 7) х=0 нүктесі бұрыштық нүкте,
функциясында (мысал 1в, лекция 7) х=0 нүктесі бұрыштық нүкте, 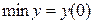 болса да.
болса да.
Анықтама 2. Функцияның туындысы нөлге тең немесе үзіліс нүктелері болатын нүктелер кризистік (стационар) нүктелер деп аталады.
Теорема 2. (Ролль). Егер 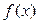 функциясы
функциясы 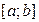 сегментінде үзіліссіз және ең болмағанда
сегментінде үзіліссіз және ең болмағанда 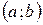 интервалында ақырлы туындылы болып,
интервалында ақырлы туындылы болып, 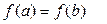 теңдігі орындалса, онда
теңдігі орындалса, онда 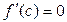 орындалатындай
орындалатындай 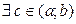 .
.
Дәлелдеуі. 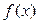 функциясы
функциясы 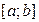 сегментінде үзіліссіз болғандықтан,
сегментінде үзіліссіз болғандықтан, 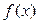 функциясы осы аралықта өзінің ең кіші мәні m мен ең үлкен мәні М –ді қабылдайды. Онда, егер m=M
функциясы осы аралықта өзінің ең кіші мәні m мен ең үлкен мәні М –ді қабылдайды. Онда, егер m=M 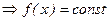 ,
, 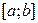 аралығында
аралығында 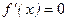 .
. 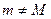 болсын және
болсын және 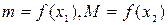 . Онда х1 және х2 нүктелерінің біреуі
. Онда х1 және х2 нүктелерінің біреуі 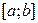 интервалының шеткі нүктелеріне тең емес. Ол нүкте
интервалының шеткі нүктелеріне тең емес. Ол нүкте 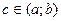 нүктесі болсын. Ендеше, c нүктесі экстремум нүктесі болғандықтан,
нүктесі болсын. Ендеше, c нүктесі экстремум нүктесі болғандықтан, 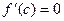 (сурет15).
(сурет15).
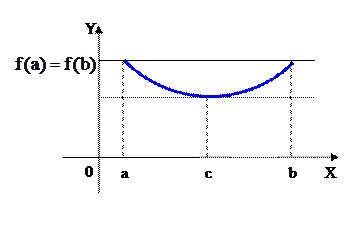 |
Сурет 15
Теорема 3 (Коши). Егер 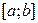 аралығында
аралығында 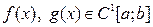 және
және 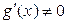 болса, онда
болса, онда 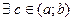
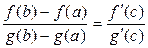
Келесі теорема 3 теореманың салдары сияқты қарастырылады.
Теорема 4 (Лагранж теоремасы)
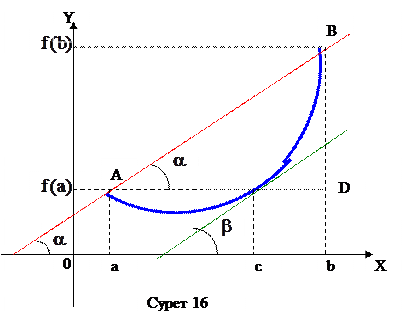 Егер
Егер 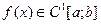 , онда
, онда 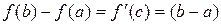 теңдігі орындалатындай
теңдігі орындалатындай 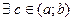 (сурет 16).
(сурет 16).
Салдар 1. Егер 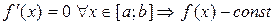 , [a;b] аралығында.
, [a;b] аралығында.
Салдар 2. Егер 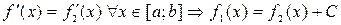 , [a;b] аралығында, мұндағы С – const.
, [a;b] аралығында, мұндағы С – const.
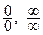 түріндегі анықталмағандықтарды ашу. Лопиталь ережесі
түріндегі анықталмағандықтарды ашу. Лопиталь ережесі
Бұл ереже 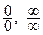 түріндегі дифференциалданатын функцияның шектерін туынды көмегімен есептеуге мүмкіндік береді.
түріндегі дифференциалданатын функцияның шектерін туынды көмегімен есептеуге мүмкіндік береді.
Мысал 1.
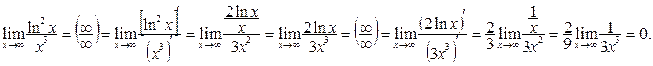 (8)-ші формуланың сол жағынның шегі табылуы мүмкін, ал оң жағының шегі – табылмайды.
(8)-ші формуланың сол жағынның шегі табылуы мүмкін, ал оң жағының шегі – табылмайды.
Мысал 2.
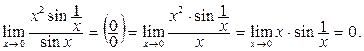
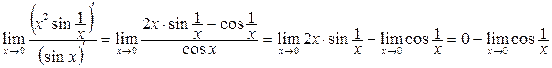 - шегі табылмайды.
- шегі табылмайды.
Мысал 3. 
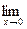
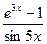 шегін есепте.
шегін есепте.
Берілген бөлшектің алымы мен бөлімі үзіліссіз, дифференциалданатын және нөлге ұмтылатын функция. Яғни, Лопиталь ережесін екі рет қолдана аламыз:

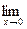
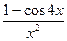
 =
= 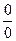 =
= 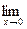
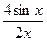 =
= 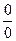 =
= 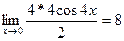 .
.
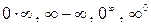 анықталмағандықтарын ашу
анықталмағандықтарын ашу
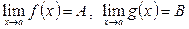 болсын. Онда
болсын. Онда
а) 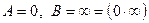 . Бұл жағдайда
. Бұл жағдайда 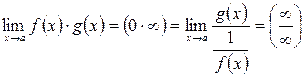 .
.
Мысал 4. 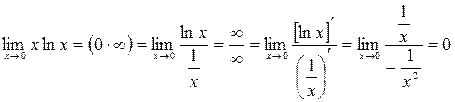 .
.
б) 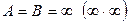 . Онда
. Онда 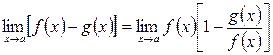 .
.
Мысал 5. 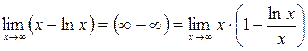 .
.
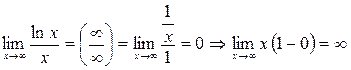 .
.
в) 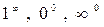 анықталмағандықтары
анықталмағандықтары 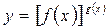 өрнегінен шығады және теңдіктің екі жағын да логарифмдеу арқылы
өрнегінен шығады және теңдіктің екі жағын да логарифмдеу арқылы 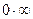 анықталмағандық түріне келтіреміз.
анықталмағандық түріне келтіреміз.
Мысал 6.
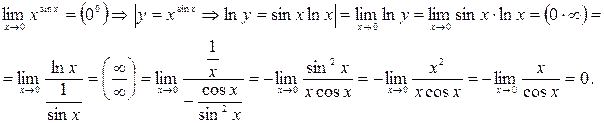
Немесе 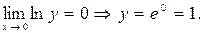
Дата публикования: 2014-10-19; Прочитано: 3631 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
