 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Хаотическая динамика. Примеры хаотических систем
|
|
Тео́рия ха́оса — математический аппарат, описывающий поведение некоторых нелинейных динамических систем, подверженных при определённых условиях явлению, известному как хаос. Поведение такой системы кажется случайным, даже если модель, описывающая систему, является детерминированной.
Примерами подобных систем являются атмосфера, турбулентные потоки, биологические популяции, общество как система коммуникаций и его подсистемы: экономические, политические и другие социальные системы. Их изучение, наряду с аналитическим исследованием имеющихся рекуррентных соотношений, обычно сопровождается математическим моделированием, эффект Коновала — распределение частот выпадения положительных результатов, или принятия правильных решений.
Теория хаоса — область исследований, связывающая математику и физику.
Динамическая система, процессы в которой характеризуются странным аттрактором, является хаотической системой. Динамическая система хаотична тогда и только тогда, когда у нее существует незамкнутая фазовая траектория. В отличие от устойчивой динамической системы определить состояние хаотической системы по заданным значениям времени и начальных условий невозможно.
Приведем примеры моделей хаотических систем.
1. 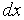 /
/ 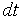 =
= 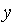 +
+ 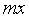 -
- 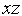 ,
,
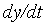 =-
=- 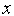 ,
,
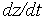 =-
=- 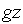 -
- 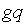 (
(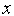 )
) 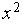 ,
,
где 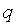 (
(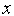 )= 0 при
)= 0 при 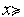 0 и
0 и 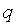 (
(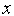 )=1 при
)=1 при 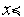 0.
0.
2. Система уравнений Лоренца — трехмерная система нелинейных дифференциальных уравнений первого порядка вида
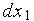 /
/ 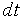 = –
= – 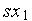 +
+ 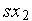 ,
,
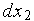 /
/ 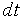 = –
= – 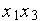 +
+ 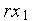 –
– 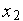 , (1)
, (1)
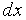 3/
3/ 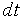 =
= 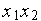 –
– 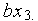
В ней s, b и r — параметры. Эта система возникла в задаче о моделировании конвективного течения жидкости, подогреваемой снизу. Такое течение описывается системой дифференциальных уравнений в частных производных. Система (1) получается из нее проектированием на специальное трехмерное подпространство.
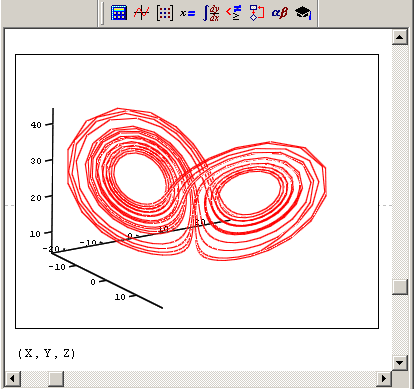
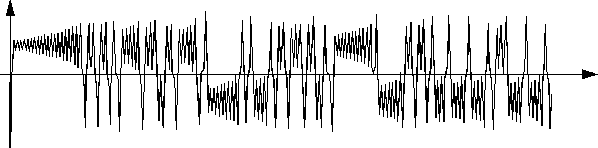
В результате численного интегрирования системы (1) Э. Лоренц обнаружил, что при s = 10, b = 8/3 и r = 28 у этой динамической системы, с одной стороны, наблюдается хаотическое, нерегулярное поведение всех траекторий и все траектории притягиваются к аттрактору рис. 1. На рис. 2 приведена зависимость 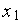 от времени.
от времени.
|
Рис. 1. Пример странного аттрактора (для задачи Лоренца)
|
Рис. 2. Хаотические колебания (зависимость переменной x 1 от времени в задаче Лоренца)
Переход к динамическому хаосу в классических трехмерных диссипативных системах обыкновенных дифференциальных уравнений. Системы Лоренца, Ресслера, Чуа, Магницкого. Многомерные нелинейные системы обыкновенных дифференциальных уравнений.
СИСТЕМА ЛОРЕНЦА.
dx/dt= -a*x+a*y, a>0
dy/dt= r*x-y-x*z, r>0
dz/dt= -b*z+x*y, b>0
Уравнения подвергались всестороннему изучению многими авторами, начиная с Лоренца, который проинтегрировал их численно, используя фиксированные значения управляющих параметров a =10, b=8/3 и единственный переменный управляющий параметр r.
При 0< r<1 (рис.1) имеем только одну критическую точку. Она является одновременно локальным и глобальным аттрактором. Другими словами, любое начальное состояние будет приближаться к началу координат при t стремящемся к бесконечности. Когда r становится близким к единице, возникает критическое замедление, а при достижении величиной r значения +1 начало координат теряет устойчивость и от него ответвляются два аттрактора, причем оба глобально и локально устойчивы. В случае r<1.345 равновесия - узлы, r >1.345 - фокусы.
При увеличении r до величины 13.926 две неустойчивые траектории, исходящие из начала координат, возвращаются в начало координат при t стремящемся к бесконечности, при этом перестают быть глобальными аттракторами. Напротив, они окружены; окрестностями, в которых являются локальными. Точка, исходящая из области, лежащей вне этих окрестностей, может совершать колебательные движения из одной окрестности в другую и обратно. Такое поведение называют метастабильным хаосом (рис.2).
При r =24.74 возникает инверсия бифуркации Хопфа, при r > 24.74 остается "странный аттрактор" (рис.3). При больших r в системе существует симметричный цикл (рис.6 - r=400). Далее при уменьшении параметра происходит бифуркация потери симметрии и в системе существуют два несимметричных периодических решения (рис.5 - r=300), затем происходит каскад бифуркации удвоения (рис.4 - r=225).
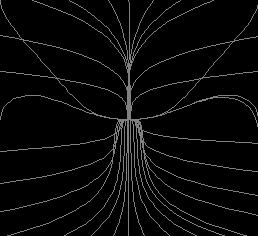
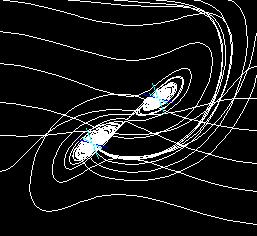

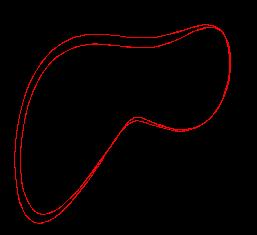
Каждая из основных областей классической физики создала свою модель хаотической динамики: гидромеханика - уравнения Лоренца строительная механика - аттрактор Дуффинга-Холмса с двумя потенциальными ямами, электротехника - аттрактор Дуффинга-Уэды.
Еще одна простая модель возникла в динамике химических реакций, протекающих в некоторой смеси с перемешиванием. Предложил ее Ресслер:
dx/dt=-(y+z)
dy/dt=x+a*y
dz/dt=b+z*(x-c)
Эти уравнения часто исследовались при a=b=0.2. Периодические движения с периодами 1,2 и 4 могут быть обнаружены при c=2.6; 3.5 и 4.1 соответственно (см. рис.1, 2, 3). При c > 4.23 могут встретиться хаотические движения (рис.4).
Модель Ресслера обладает свойствами линейного осциллятора с отрицательным коэффициентом затухания и обратной связью
y''-a*y'+y=-z.
Она служит примером многомерных систем, динамика которых допускает аппроксимацию одномерным отображением. Если провести сечение Пуанкаре при y=0 и построить на плоскости (x,z) одномерное отображение из точек Хn,т.е. построить график зависимости Хn+1 от Xn, то обращает на себя внимание сходство полученной кривой с квадратичным, или логистическим, отображением. В модели Ресслера наблюдается удвоение периода.
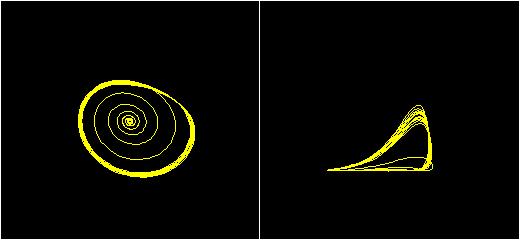
Цепь Чуа - http://ru.wikipedia.org/wiki/%D0%A6%D0%B5%D0%BF%D1%8C_%D0%A7%D1%83%D0%B0
Классический геометрический подход к объяснению явления динамического хаоса. Гиперболическая теория. Отображение подковы Смейла, отображение Хенона, соленоид Смейла-Вильямса. Фракталы. Фрактальная размерность. Теория гомоклинического хаоса.
Подкова Смейла — предложенный Стивом Смейлом пример динамической системы, имеющей бесконечное число периодических точек (и хаотическую динамику), причём это свойство не разрушается при малых возмущениях системы.
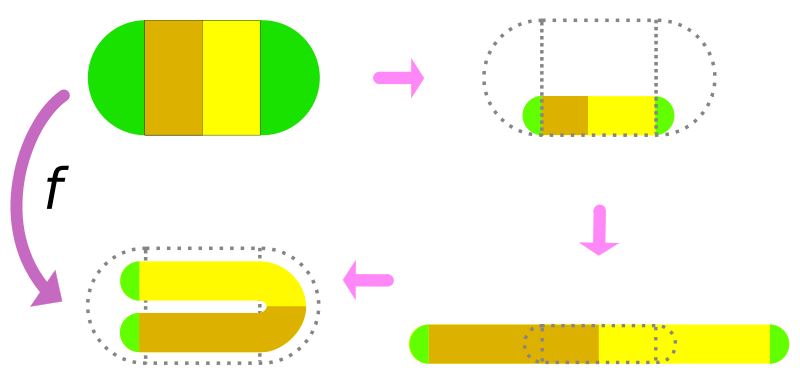
Соленоид Смейла — Вильямса — пример обратимой динамической системы, аналогичной по поведению траекторий отображению удвоения на окружности. Более точно, эта динамическая система определена на полнотории, и за одну её итерацию угловая координата удваивается; откуда автоматически возникает экспоненциальное разбегание траекторий и хаотичность динамики. Также соленоидом называют и максимальный аттрактор этой системы (откуда, собственно, и происходит название): он устроен как (несчётное) объединение «нитей», наматывающихся вдоль полнотория.
Дата публикования: 2014-10-19; Прочитано: 4549 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
