 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема 5.1 (Форда-Фалкерсона)
|
|
Максимальный поток в сети равен минимальной пропускной способности разреза:
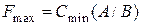 .
.
Доказательство теоремы представляет алгоритм определения максимального потока по сети.
Алгоритм нахождения максимального потока на сети:
Этап 1. Насыщение потока.
Шаг 1. Сформировать произвольный начальный поток.
Шаг 2. Найти оставшиеся возможные пути из истока 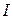 в сток
в сток 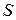 , имеющие только ненасыщенные дуги. Если такой путь найден, то переходим к шагу 3. Если путь не найден, то переходим к шагу 4.
, имеющие только ненасыщенные дуги. Если такой путь найден, то переходим к шагу 3. Если путь не найден, то переходим к шагу 4.
Шаг 3. Увеличить поток по найденному пути таким образом, чтобы, по крайней мере, одна из дуг стала насыщенной.
Шаг 4. Получившийся поток насыщен.
Этап 2. Пометка вершин сети (перераспределение потока).
Шаг 5. Вершину 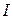 пометить
пометить 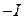 .
.
Шаг 6. Пусть 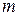 – любая из уже помеченных вершин,
– любая из уже помеченных вершин, 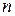 – произвольная непомеченная вершина, смежная с вершиной
– произвольная непомеченная вершина, смежная с вершиной 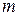 . Вершину
. Вершину 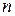 помечаем
помечаем 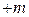 , если данные вершины соединены ненасыщенной дугой
, если данные вершины соединены ненасыщенной дугой 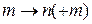 , и помечаем
, и помечаем 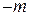 , если соединены непустой дугой
, если соединены непустой дугой 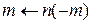 .
.
После пометки вершин возможны два случая: вершина 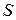 оказалась либо помеченной, либо непомеченной.
оказалась либо помеченной, либо непомеченной.
Шаг 7. Вершина 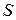 оказалась помеченной. Значит, существует последовательность помеченных вершин от истока
оказалась помеченной. Значит, существует последовательность помеченных вершин от истока 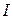 к стоку
к стоку 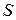 . В этой последовательности каждая последующая вершина помечена буквой предыдущей вершины. На дугах последовательности определяем новый поток. Увеличиваем на
. В этой последовательности каждая последующая вершина помечена буквой предыдущей вершины. На дугах последовательности определяем новый поток. Увеличиваем на 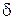 единиц поток на дугах, имеющих направление от
единиц поток на дугах, имеющих направление от 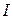 к
к 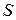 и уменьшаем на
и уменьшаем на 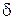 единиц поток на дугах, имеющих обратное направление. Число
единиц поток на дугах, имеющих обратное направление. Число 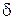 равно наименьшей разнице между пропускной способностью и потоком дуг, входящих в последовательность. Заметим, что поток можно увеличивать (уменьшать) на прямых (обратных) дугах до тех пор, пока одна из дуг не станет насыщенной (пустой). Далее вновь переходим к пометке вершин (шаг 5). Перераспределение потока сохраняет все его свойства и увеличивает поток на
равно наименьшей разнице между пропускной способностью и потоком дуг, входящих в последовательность. Заметим, что поток можно увеличивать (уменьшать) на прямых (обратных) дугах до тех пор, пока одна из дуг не станет насыщенной (пустой). Далее вновь переходим к пометке вершин (шаг 5). Перераспределение потока сохраняет все его свойства и увеличивает поток на 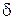 единиц в вершину
единиц в вершину 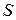 .
.
Этап 3. Определение максимального потока.
Шаг 8. Вершина 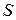 осталась непомеченной. Пусть
осталась непомеченной. Пусть 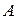 – множество всех помеченных вершин,
– множество всех помеченных вершин, 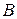 – множество всех непомеченных вершин. Тогда дуги, связывающие два подмножества вершин
– множество всех непомеченных вершин. Тогда дуги, связывающие два подмножества вершин 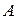 и
и 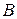 , определяют разрез
, определяют разрез 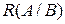 . Таким образом, найден поток
. Таким образом, найден поток 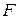 и разрез
и разрез 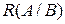 , для которого выполняется условие
, для которого выполняется условие 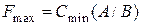 .
.
Пример 5.2. На сети из примера 5.1. сформировать максимальный по величине поток, направленный из истока 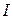 в сток
в сток 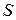 . Выписать ребра, образующие на сети разрез минимальной пропускной способности.
. Выписать ребра, образующие на сети разрез минимальной пропускной способности.
Решение.
Этап 1.
Шаг 1. Воспользуемся тем, что в примере 5.1 уже был сформирован некоторый поток на сети, рис. 5.2.
Шаг 2. Путь 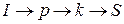 содержит насыщенную дугу
содержит насыщенную дугу 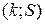 . Добавить потока по этому пути больше нельзя. Пути
. Добавить потока по этому пути больше нельзя. Пути 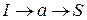 ,
, 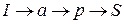 и
и 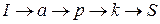 содержат насыщенные дуги.
содержат насыщенные дуги.
Но путь 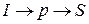 имеет две дуги, которые еще ненасыщенные.
имеет две дуги, которые еще ненасыщенные.
Шаг 3. Увеличим поток по найденному пути на величину: 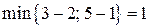 , т.е. на 1 единицу. В результате − дуга
, т.е. на 1 единицу. В результате − дуга 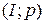 стала насыщенной, рис. 5.3.
стала насыщенной, рис. 5.3.
Шаг 4. Таким образом, получаем насыщенный поток, поскольку каждый рассмотренный путь содержит хотя бы одну насыщенную дугу.
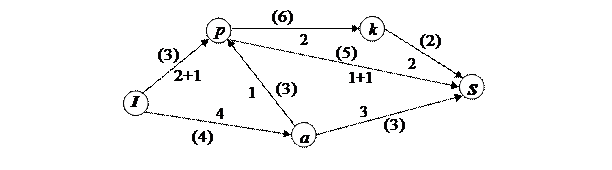
Рис. 5.3
Этап 2.
Выясним, является ли построенный поток максимальным по величине. Строим сеть, на которой отметим все вершины и ненасыщенные дуги. На этой сети разность пропускных способностей дуги и проходящего по ней потока обозначим числом в квадратных скобках.
Шаг 5, 6. Вершину 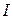 пометим
пометим 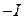 . На шаге 6 предусматривается пометка вершин, смежных с вершиной
. На шаге 6 предусматривается пометка вершин, смежных с вершиной 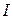 , соединенных ненасыщенными дугами. Но на построенной сети таких вершин нет.
, соединенных ненасыщенными дугами. Но на построенной сети таких вершин нет.
В результате вершина 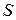 оказалась непомеченной, рис. 5.4.
оказалась непомеченной, рис. 5.4.
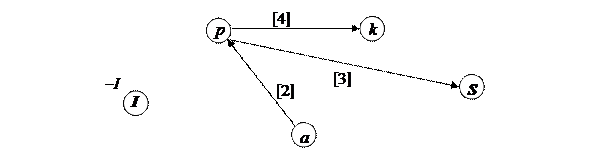
Рис. 5.4
Этап 3.
Шаг 8. Так как вершина 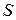 непомеченная, то поток, сформированный на сети, получился максимальным.
непомеченная, то поток, сформированный на сети, получился максимальным.
Строим разрез на сети. Разбиваем множество вершин на два подмножества: 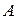 и
и 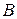 . Так как только одна вершина оказалась помеченной, то множество
. Так как только одна вершина оказалась помеченной, то множество 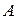 состоит из одной вершины − истока
состоит из одной вершины − истока 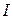 , а остальные вершины образуют множество
, а остальные вершины образуют множество 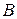 :
:
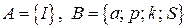 .
.
Проводим разрез 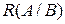 , который состоит из дуг
, который состоит из дуг 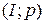 и
и 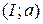 , рис. 6.5:
, рис. 6.5:
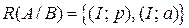 .
.
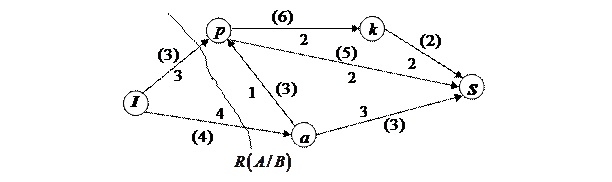
Рис. 5.5
Определим величину максимального потока 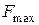 :
:
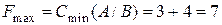 (ед.),
(ед.),
Пример 5.3. На заданной сети в скобках указаны пропускные способности дуг, рис. 5.6. Требуется сформировать на сети максимальный поток, направленный из истока 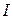 в сток
в сток 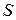 , и выписать ребра, образующие на сети разрез минимальной пропускной способности.
, и выписать ребра, образующие на сети разрез минимальной пропускной способности.
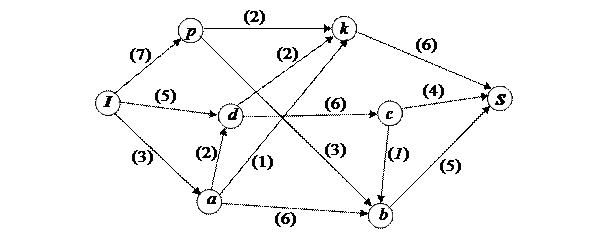
Рис. 5.6
Решение.
Этап 1.
Сформируем на сети начальный поток. Рассмотрим путь 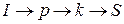 . Поскольку
. Поскольку 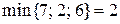 , по этому пути пропускаем поток в 2 единицы. На сети значение потока обозначим числами без скобок. По пути
, по этому пути пропускаем поток в 2 единицы. На сети значение потока обозначим числами без скобок. По пути 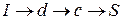 пропускаем поток в 4 единицы, так как
пропускаем поток в 4 единицы, так как 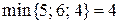 . По пути
. По пути 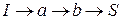 пропускаем поток в 3 единицы, так как
пропускаем поток в 3 единицы, так как 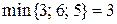 . Таким образом, начальный поток имеет вид:
. Таким образом, начальный поток имеет вид:
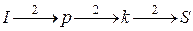 ,
,
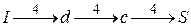 ,
,
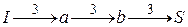 .
.
Начальный поток изображен на рис. 5.7.
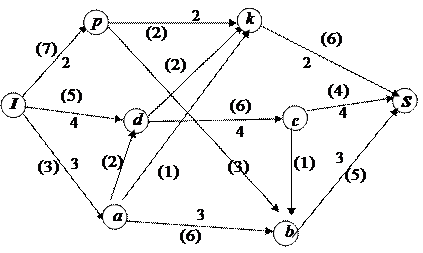 |

Рис. 5.7
Каждый из рассмотренных путей содержит насыщенную дугу, поэтому эти пути насыщенные. На сети есть еще пути, которые содержат ненасыщенные дуги, а именно: 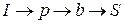 ,
, 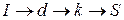 и
и 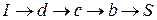 . Для первого пути дополнительно увеличим поток на 2 единицы, так как
. Для первого пути дополнительно увеличим поток на 2 единицы, так как 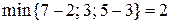 . Второй и третий пути содержат одну и ту же дугу
. Второй и третий пути содержат одну и ту же дугу 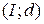 с минимальной для них оставшейся разностью
с минимальной для них оставшейся разностью 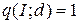 . Поэтому для увеличения потока на 1 единицу выберем, например, путь
. Поэтому для увеличения потока на 1 единицу выберем, например, путь 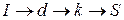 .
.
Теперь каждый из этих путей содержит насыщенную дугу, следовательно, полученный поток – насыщенный, рис. 5.8.
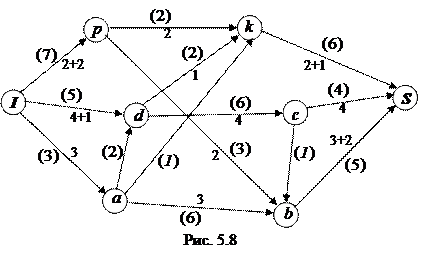
Выясним, является ли построенный поток максимальным. Изобразим сеть, на которой отметим все вершины и ненасыщенные дуги. На этой сети разность пропускной способности дуги и проходящего по ней потока обозначим числом в квадратных скобках. Пропускную способность дуги, по которой поток не проходит, оставим в круглых скобках, рис. 5.9.
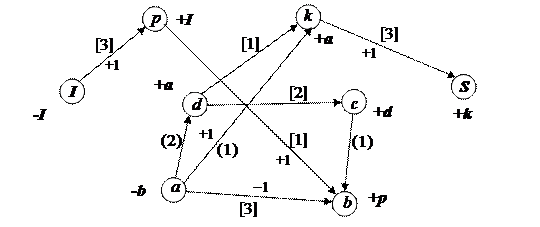
Рис. 5.9
Согласно рис. 5.9 на сети исток 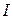 и сток
и сток 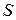 связаны дугами. Значит, можно добавить какое-то количество потока по ненасыщенным дугам, при этом придется перераспределить поток.
связаны дугами. Значит, можно добавить какое-то количество потока по ненасыщенным дугам, при этом придется перераспределить поток.
Этап 2.
На построенной сети помечаем вершины. Вершину 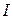 пометим
пометим 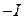 . Смежную ей вершину
. Смежную ей вершину 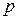 пометим
пометим 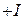 , так как эти вершины соединяет ненасыщенная дуга
, так как эти вершины соединяет ненасыщенная дуга 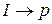 . Вершину
. Вершину 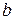 помечаем
помечаем 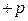 , так как вершины
, так как вершины 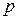 и
и 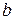 соединяет ненасыщенная дуга
соединяет ненасыщенная дуга 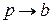 . Вершину
. Вершину 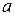 помечаем
помечаем 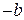 , так как вершины
, так как вершины 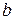 и
и 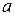 соединяет непустая дуга
соединяет непустая дуга 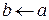 . Вершины
. Вершины 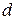 и
и 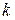 помечаем
помечаем 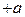 , так как они соединены с вершиной
, так как они соединены с вершиной 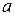 ненасыщенными дугами
ненасыщенными дугами 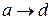 и
и 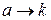 . Вершина
. Вершина 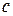 смежная вершине
смежная вершине 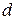 , и эти вершины соединены ненасыщенной дугой
, и эти вершины соединены ненасыщенной дугой 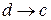 , поэтому вершину
, поэтому вершину 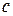 помечаем
помечаем 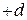 . Вершина
. Вершина 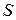 смежная вершине
смежная вершине 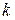 , и эти вершины соединены ненасыщенной дугой
, и эти вершины соединены ненасыщенной дугой 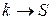 , поэтому вершину
, поэтому вершину 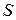 помечаем
помечаем 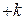 .
.
Вершина 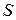 оказалась помеченной. Значит, существует последовательность помеченных вершин от
оказалась помеченной. Значит, существует последовательность помеченных вершин от 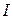 к
к 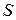 :
: 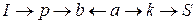 . В этой последовательности каждая последующая вершина помечена буквой предыдущей вершины. Перераспределим поток на этом пути. Определим число
. В этой последовательности каждая последующая вершина помечена буквой предыдущей вершины. Перераспределим поток на этом пути. Определим число 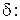
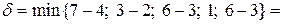
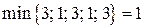 .
.
Увеличим на 1 единицу поток на дугах, имеющих направление от 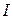 к
к 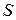 :
: 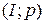 ,
, 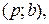
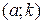 ,
, 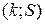 . Уменьшим на 1 единицу поток на дугах, имеющих обратное направление:
. Уменьшим на 1 единицу поток на дугах, имеющих обратное направление: 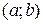 . Получим следующую сеть с новым сформированным потоком, который изображен на рисунке 5.10.
. Получим следующую сеть с новым сформированным потоком, который изображен на рисунке 5.10.
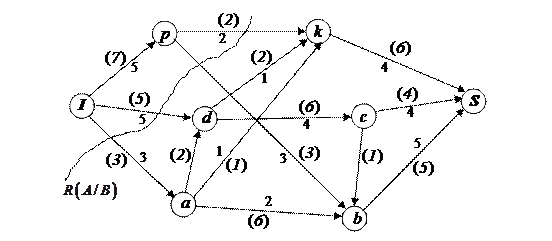
Рис. 5.10
Проверим, будет ли построенный поток максимальным. Изобразим сеть, на которой отметим все вершины и ненасыщенные дуги, рис. 5.11.
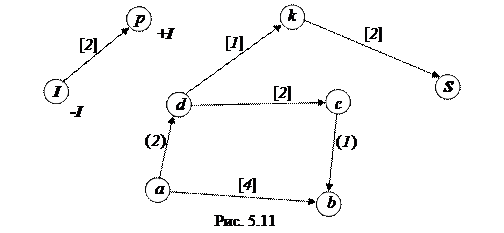
Вновь пометим вершины. Вершину 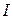 пометим
пометим 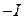 . Смежную ей вершину
. Смежную ей вершину 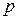 пометим
пометим 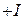 , так как эти вершины соединяет ненасыщенная дуга
, так как эти вершины соединяет ненасыщенная дуга 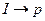 . Все остальные вершины, в том числе и вершина
. Все остальные вершины, в том числе и вершина 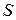 , остаются непомеченными. Значит, поток на сети максимальный.
, остаются непомеченными. Значит, поток на сети максимальный.
Этап 3.
Согласно рис. 5.11, на последней сети исток 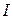 и сток
и сток 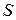 не связны дугами. Значит поток, изображенный на рис. 5.10, является максимальным.
не связны дугами. Значит поток, изображенный на рис. 5.10, является максимальным.
Строим разрез на сети. Разбиваем множество вершин на два подмножества: 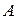 и
и 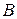 . Помеченные вершины образуют множество
. Помеченные вершины образуют множество 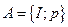 , непомеченные – множество
, непомеченные – множество 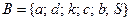 . Проводим разрез
. Проводим разрез 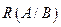 , который состоит из дуг
, который состоит из дуг 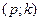 ,
, 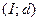 ,
, 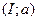 ,
, 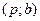 :
:
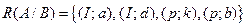 .
.
Определим величину максимального потока 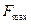 :
:
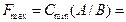
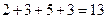 (ед.).
(ед.).
Ответ: мощность максимального потока составляет 13 ед., разрез минимальной пропускной способности образуют ребра 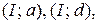
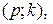
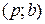 .
.
,
Дата публикования: 2014-10-19; Прочитано: 1917 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
