Ременные вариаторы

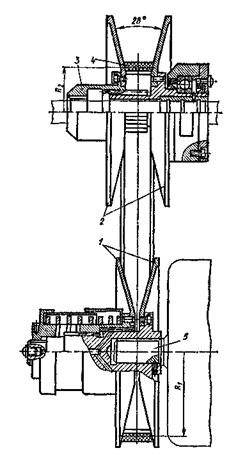
Этот тип вариаторов может быть выполнен как с плоским ремнем, так и с ремнем клинообразного сечения. В настоящее время клиноременные вариаторы для малых и средних мощностей наиболее перспективны. Клиноременные вариаторы со стандартным ремнем просты по конструкции и надежны в работе; применяются преимущественно встроенными и легко комбинируются с другими узлами машины. На рис. 11.4 представлена конструкция такого вариатора, используемого в качестве привода станка. Вариатор выполнен в виде обособленных узлов ведущего и ведомого шкивов, охваченных ремнем.

Рис. 11.4.

Узел ведущего шкива 1 закреплен консольно на валу электродвигателя, а ведомого 2 – на двух опорах или консольно. Регулирование скорости в рассматриваемом вариаторе производится путем перемещения стакана 3 подвижного ведомого шкива. В зависимости от осевого положения дисков управляемого шкива 2 ремень 4 перемещается в радиальном направлении шкивов, изменяются радиусы R₁ и R₂, а следовательно, и передаточное отношение. Диски ведущего шкива 1 подпружинены и занимают соответствующее положение в зависимости от перемещения ремня.

Перечень вопросов для контроля знаний:

1. Что учитывается коэффициентом скольжения?

2. Назовите основные критерии работоспособности фрикционных передач.

3. Запишите формулу для определения межосевого расстояния фрикционной передачи.

4. Запишите формулу Герца для определения контактных напряжений.

5. Запишите формулу для определения межосевого расстояния в проектировочном расчете для материалов с упругими свойствами.

6. Как определяется приведенный модуль упругости?

7. Запишите формулу для расчета по нагрузке на единицу длины контактной линии (по погонной нагрузке).

8. Запишите формулу для определения межосевого расстояния в проектировочном расчете для материалов, не обладающих упругими свойствами.

9. Укажите основные особенности конусного вариатора.

10. Укажите основные особенности лобового вариатора.

11. Укажите основные особенности дискового вариатора.

12. Укажите основные особенности ременного вариатора.

Занятие 14, 15. Практическая работа 2.

«Геометрический и силовой расчет фрикционной передачи».

Вариант 1.

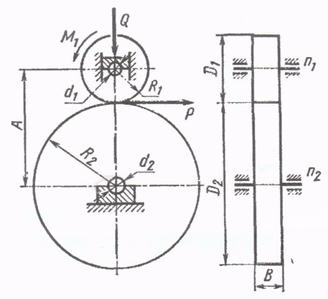
Определить мощность, которую может передавать фрикционная передача цилиндрическими катками.

Дано: частота вращения ведущего вала n₁ = 1450 об/мин;

D₁ = 40 мм;

D₂ = 100 мм;

В = 20 мм;

Материал катков – сталь ШХ 15, твердость HRC 60.

Передача работает со смазкой.

Занятие 16. Лекция 12.

Содержание лекции.

6. Общие сведения и кинематические характеристики зубчатых передач.

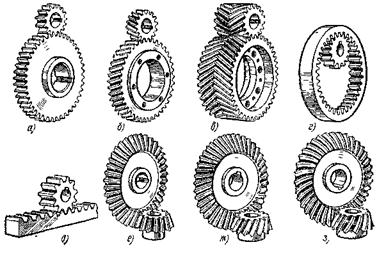
1. В современном машиностроении и приборостроении наиболее распространенным типом механических передач являются зубчатые передачи. Зубчатые передачи предназначены для передачи движения с соответствующим изменением угловой скорости (момента) по величине и направлению. В этих передачах движение передается с помощью зацепления пары зубчатых колес. (рис. 12.1.). Меньшее из зубчатых колес сцепляющейся пары называется шестерней, а большее колесом. Термин «зубчатое колесо» относится как к шестерне, так и к колесу.

Буквенные обозначения, общие для обоих зубчатых колес сцепляющейся пары, отмечают индексом 1 для шестерни и индексом 2 для колеса (например, число зубьев z₁ и z₂).

Рис. 12.1.

Оценка и применение. Из всех видов передач зубчатые имеют наименьшие габаритные размеры и потери на трение. Коэффициент потерь мощности одной зубчатой пары при тщательном выполнении и надлежащей смазке не превышает обычно 0,01; зубчатые передачи используются при мощностях, начиная от ничтожно малых (в приборах) до измеряемых десятками тысяч киловатт. Передаваемые моменты достигают 5 · 10⁶ Н · м. Диаметры колес судовых установок, например, в передачах на гребной винт достигают 6 м. Зубчатые передачи могут работать в самых разнообразных условиях с окружными скоростями от ничтожно малых до 150 м/с и обеспечивают передачу движения между произвольно расположенными в пространстве валами без проскальзывания (с постоянным передаточным отношением).

Преимущества зубчатых передач: надежность работы в широком диапазоне нагрузок и скоростей; компактность; долговечность; высокий КПД (0,96…0,99); сравнительно малые нагрузки на валы и подшипники; постоянство передаточного отношения; простота обслуживания.

Недостатки зубчатых передач: высокие требования к точности изготовления и монтажа; шум при больших скоростях; большая жесткость, не позволяющая компенсировать динамические нагрузки.

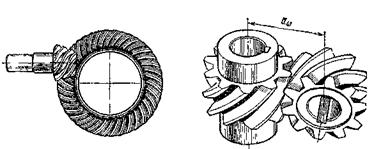
Рис. 12.2 Рис. 12.3

Классификация зубчатых передач. Зубчатые передачи и колеса классифицирую по следующим признакам.

1. По взаимному расположению геометрических осей валов зубчатых колес: цилиндрические – при параллельных осях, зацепление может быть как внемним, так и внутренним (см. рис. 12.1, а, б, в, г); конические – при пересекающихся осях (см. рис. 12.1, е, ж, з); гипоидные конические передачи – при перекрещивающихся осях (рис. 12.2); винтовые – цилиндрические передачи с перектещивающимися осями (рис. 12.3).

Для преобразования вращательного движения в поступательное и наоборот применяется реечная передача (см. рис. 12.1, д), которая является частным случаем цилиндрической зубчатой передачи. Рейку рассматривают как колесо, диаметр которого обращается в бесконечность.

2. По расположению зубьев относительно образующей колес: прямозубые (см. рис 12.1, а, г, д, е), косозубые (см. рис. 12.1. б, ж), шевронные (см. рис. 12.1, в) и с криволинейными зубьями (см. рис. 12.1, з).

При переходе от прямозубых передач к непрямозубым повышается плавность работы, уменьшается шум и увеличивается нагрузочная способность. Поэтому указанные передачи используют при более высоких скоростях и передаче больших моментов.

3. По форме бокового профиля зубьев: эвольвентные, циклоидальные и круговые (зацепление Новикова).

4. По конструктивному исполнению различают открытые и закрытые передачи. В открытых передачах зубья колес работают всухую или периодически смазываются пластичным смазочным материалом и не защищены от внешней среды. Закрытые передачи размещают в специальном корпусе, защищающем от проникновения пыли извне, с постоянным смазыванием погружением (из масляной ванны корпуса) или проточным смазыванием мест зацепления зубьев.

Кинематическая характеристика зубчатой передачи. Зубчатый механизм, состоящий из двух зубчатых колес и стойки, называется зубчатой передачей. Зубчатый механизм, состоящий из трех или более зубчатых колес (с неподвижными осями) и стойки, называется зубчатым рядом. Основной кинематической характеристикой зубчатой передачи, как и зубчатого ряда, в общем случае является передаточное отношение.

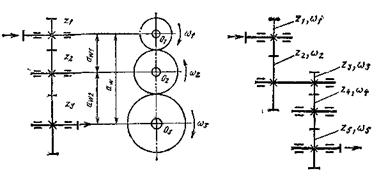
В зависимости от расположения сопряженных зубчатых колес различают одноступенчатый зубчатый ряд (рис. 12.4) и многоступенчатый зубчатый ряд (рис. 12.5). Ступень зубчатого ряда – это сочетание зубчатых колес, на которых происходит изменение угловой скорости.

Рис. 12.4 Рис. 12.5

Все зубчатые колеса в любом зубчатом ряду можно разделить на ведущие, ведомые и промежуточные. Ведущие – это такие колеса, которые получают движение через вал, а передают – через зубья. В изображенных зубчатых рядах к ведущим колесам относятся z₁ (см.рис. 12.4) и z₁ и z₃ (см. рис. 12.5). Ведомые – это такие колеса, которые получают движение от зубьев, а передают валу. К ведомым колесам относятся z₃ (см. рис. 12.4) и z₂ и z₅ (см. рис. 12.5). Промежуточные колеса получают и передают движение через зубья. К таким колесам относятся z₂ (см. рис. 12.4) и z₄ (см. рис. 12.5). Промежуточные колеса могут сидеть на своих осях свободно, так как ось не участвует в передаче движения. Ведущие и ведомые колеса должны сидеть навалу жестко, т.е. вращаться вместе с валом.

Одноступенчатый зубчатый ряд (см. рис. 12.4) можно условно представить как состоящий из двух зубчатых передач z₁ и z₂, z₂ и z₃. Выразим передаточное отношение зубчатого ряда через передаточные отношения зубчатых передач, входящих в него. Из первой передачи найдем угловую скорость ω₂ второго колеса

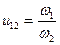и .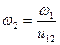

Запишем передаточное отношение для второй передачи и подставим в него найденное значение ω₂:

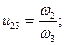
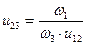, откуда получим .

В общем случае для ряда из n колес будем иметь

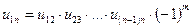, (12.1)

где m – число зубчатых передач внешнего зацепления, входящих в зубчатый ряд.

Учитывая, что для зубчатой передачи передаточное отношение численно равно передаточному числу, выразим передаточное отношение зубчатого ряда через числа зубьев колес, входящих в него.

Подставив передаточные отношения 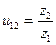и 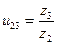в формулу (12.1), получим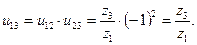

Из полученного видно, что промежуточные колеса в одноступенчатых зубчатых рядах не влияют на величину передаточного отношения. Их вводят при необходимости получения требуемых значений межосевого расстояния а_ω и знака передаточного отношения (т.е. направления вращения). Изложенное относится и к многоступенчатым зубчатым рядам при оценке передаточного отношения каждого их ряда – ступени.

Многоступенчатый зубчатый ряд. Рассмотрим зубчатый ряд, приведенный на рис. 12.5, который состоит из трех зубчатых передач z₁ и z₂, z₃ и z₄, z₄ и z₅. Выразим передаточное отношение u₁₅ зубчатого ряда через передаточные отношения зубчатых передач, входящих в него:

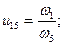
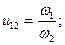
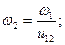
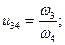
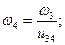
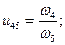
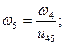
Учитывая, что ω₂ = ω₃, можно записать

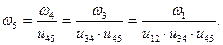
Подставляя значение ω₅ в выражение для u₁₅, получим ,

или в общем случае (для любого зубчатого ряда) будем иметь

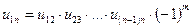, т.е. получено выражение, аналогичное выражению (12.1).

Таким образом, передаточное отношение любого зубчатого ряда равно произведению передаточных отношений всех передач, входящих в зубчатый ряд.

Выразим передаточное отношение зубчатого ряда через числа зубьев колес, входящих в зубчатый ряд. Подставив передаточные отношения

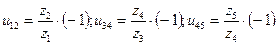в выражение (12.1), получим

После сокращения числа зубьев промежуточного колеса окончательно получим .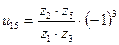

В общем случае для любого зубчатого ряда

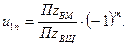
Отсюда следует, что передаточное отношение любого зубчатого ряда равно дроби, числитель которой представляет собой произведение всех чисел зубьев ведомых колес, а знаменатель – произведение всех чисел зубьев ведущих колес.

Перечень вопросов для контроля знаний:

1. Как передается движение в зубчатой передаче?

2. Какие индексы присваиваются зубчатым колесам в зубчатой передаче?

3. Укажите преимущества зубчатых передач.

4. Укажите недостатки зубчатых передач.

5. По каким признакам классифицируются зубчатые передачи?

6. Какой параметр является основной кинематической характеристикой зубчатой передачи?

7. Какие зубчатые колеса называются ведущими?

8. Какие зубчатые колеса называются ведомыми?

9. Какие зубчатые колеса называются промежуточными?

10. Что называется ступенью зубчатого ряда?

11. Чему равно передаточное отношение любого зубчатого ряда?

Занятие 17. Лекция 13.

Содержание лекции.

7. Основы теории зацепления.

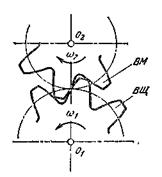
1. При работе зубчатых передач зубья одного колеса входят во впадины другого (рис.13.6), при этом боковая поверхность зуба ведущего колеса давит на боковую поверхность зуба ведомого колеса.

Профили зубьев пары колес должны быть сопряженными, т.е. заданному профилю зуба одного колеса должен соответствовать вполне определенный профиль зуба другого колеса. Чтобы обеспечить постоянство передаточного отношения, профили зубьев нужно очертить такими кривыми, которые удовлетворяли бы требованиям основной теоремы зацепления.

Теорема: общая нормаль, проведенная через точку касания двух профилей, делит межосевое расстояние на части, обратно пропорциональные угловым скоростям сопряженных колес.

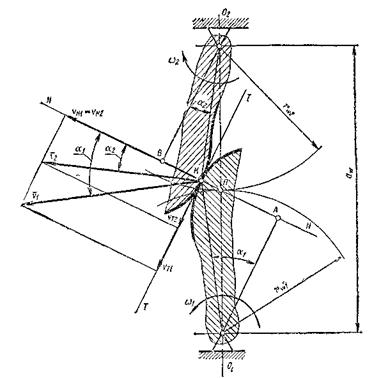
Для доказательства теоремы рассмотрим пару сопряженных зубьев в зацеплении (рис. 13.7). Профили зубьев шестерни и колеса сопрягаются в точке К, называемой точкой зацепления. Центры вращения О₁ и О₂ расположены на неизменном расстоянии а_ω друг от друга. При вращении шестерни с угловой скоростью ω₁ ее зуб давит на зуб колеса, сообщая последнему угловую скорость ω₂. Проведем через точку К общую для обоих профилей касательную ТТ и нормаль NN. Окружные скорости точки К относительно центров вращения О₁ и О₂

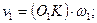
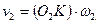
Разложим v₁ и v₂ на составляющие по направлению нормали NN и по направлению касательной ТТ:

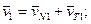
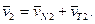
Для обеспечения постоянного касания профилей необходимо соблюдение условия v_N1 = v_N2, так как при v_N1 < v_N2 зуб шестерни отстанет от зуба колеса, а при v_N1 > v_N2 произойдет срезание зубьев.

Опустим из центров О₁ и О₂ перпендикуляры О₁А = h₁ и О₂В = h₂ на нормаль NN. Углы, образованные между перпендикуляром h₁ и линией О₁К и перпендикуляром h₂ и линией О₂К, обозначим соответственно α₁ и α₂. Так как вектор скорости v₁ перпендикулярен к линии О₁К, а вектор v_N1 перпендикулярен к линии О₁А = h₁. то угол между этими векторами будет равен α₁. Аналогично можно доказать, что угол между векторами v₂ и v_N2 будет равен α₂.

Из построений получаем

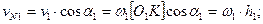
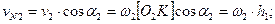
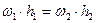или .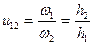

Из подобия треугольников О₁АП и О₂ВП запишем, что ,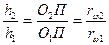

или окончательно получим 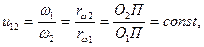что и требовалось доказать.

Рис. 13.6. Рис.13.7

Для обеспечения постоянного передаточного отношения двух профилей зубьев за период их зацепления необходимо, чтобы общая нормаль к ним в точке их касания, проведенная в любом положении соприкасающихся профилей, проходила через постоянную точку на межосевой линии, которая делит межосевое расстояние на части, обратно пропорциональные угловым скоростям.

Рис. 13.8 Рис. 13.9

Рис. 13.10 Рис. 13.11

На рис. 13.8 показаны положения, которые последовательно занимает пара сопряженных зубьев в процессе их зацепления; прямая О₁О₂ называется межосевой линией колес. Проведем в точках касания зубьев К₁, К₂ К₃ и т.д. общую нормаль NN к профилям. Она должна пересекать межосевую линию О₁О₂ в постоянной точке П (в соответствии с доказанной теоремой). Эта точка называется полюсом зацепления; ее положение на межосевой линии определяется отношением угловых скоростей колес, т.е. передаточным отношением.

Отрезок общей нормали NN, ограниченный точками А и В и являющийся траекторией общей точки контакта зубьев, называется линией зацепления зубчатой передачи.

Окружности, проходящие через полюс зацепления и обозначенные через r_ω1 и r_ω2 (см. рис. 13.7), называются начальными окружностями. При вращении зубчатых колес начальные окружности перекатываются друг по другу без скольжения, о чем свидетельствует равенство их окружных скоростей 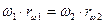, полученное из формулы (12.2). Следует иметь в виду, что незначительное изменение межосевого расстояния а_ω приведет к изменению и диаметров начальных окружностей, так как положение полюса зацепления при этом останется неизменным.

Основной закон зацепления позволяет определить, какие кривые могут служить профилями зубьев со строго постоянным передаточным отношением. В самом деле, в зацеплении все нормали к кривым, проведенным через точку касания профилей, должны проходить через полюс зацепления, т.е. должны пересекаться в одной точке. Этим свойством обладают только кривые, относящиеся к семейству рулетт.

Рулеттами называются кривые, описываемые какой-либо точкой кривой или прямой, катящейся без скольжения по другой, неподвижной кривой или прямой. Когда на перекатывающихся окружностях чертящая точка взята на самой окружности, мы получем эпициклоиду или гипоциклоиду. Качение окружности по прямой дает циклоиду, а качение прямой по окружности – эвольвенту.

Самыми простыми кривыми, относящимися к семейству рулетт, являются циклоидные кривые (эпициклоида и гипоциклоида) и эвольвента. Эти кривые и используются в качестве профилей зубьев. Сначала появилось циклоидальное зацепление. В циклоидном зубчатом колесе профиль головки зуба очерчивается по эпициклоиде, а профиль ножки зуба – по гипоциклоиде.

В эвольвентных зубчатых колесах профили зубьев очерчиваются по эвольвентам окружности с центром на оси колеса. Основным преимуществом эвольвентного зацепления является его технологичность, т.е. возможность изготовления методом обкатки (инструментом с прямолинейной режущей кромкой). Циклоидальное зацепление в основном изготовляют методом копирования, что обходится значительно дороже. Кроме того, эвольвентное зацепление допускает некоторое изменение межосевого расстояния (радиального зазора), не нарушая закона зацепления, т.е. не требует большой точности при сборке. Третьим преимуществом эвольвентного зацепления является возможность иметь сменные шестерни. Если необходимо изменить передаточное отношение, то при циклоидном зацеплении надо заменить оба зубчатых колеса, а при эвольвентном зацеплении только одно.

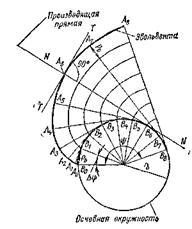
Эвольвента окружности и ее свойства. Эвольвентой называется кривая, описываемая любой точкой прямой, перекатываемой без проскальзывания по неподвижной окружности. Так, например, точка А прямой NN (рис. 13.9, точки от А₀ до А₈) опишет эвольвенту. Длина дуги окружности, которую проходит точка ее контакта с прямой NN, всегда равна длине этой прямой от точки касания с окружностью до эвольвенты (например, дуга А₀В₃ = А₃В₃). Окружность радиусом r_b, по которой перекатывается прямая NN, называется эволютой или основной окружностью, а перекатываемая прямая – производящей прямой. Для построения профиля зуба используется часть эвольвенты (рис. 13.10).

Характер эвольвентного зубчатого зацепления определяется свойствами эвольвенты.

1. Эвольвента не заходит внутрь основной окружности и представляет собой спиральную кривую, начинающуюся от основной окружности и полностью определяющуюся ее радиусом.

2. Производящая прямая NN является одновременно касательной к основной окружности и нормалью ко всем производимым ею эвольвентам. Это свойство вытекает непосредственно из построения эвольвенты.

3. Две или семейство эвольвент одной и той же основной окружности эквидистантны. Эквидистантными или равноудаленными называются две кривые, расстояние между которыми в направлении нормали везде одинаковое; назовем его шагом Р_b по основной окружности.

4. Радиус кривизны эвольвенты в любой точке равен длине касательной к основной окружности, проведенной из этой точки. Центр кривизны эвольвенты в данной точке находится на основной окружности. Это свойство также вытекает непосредственно из построения эвольвенты.

5. С увеличением радиуса r_b основной окружности эвольвента становится более пологой и при r_b → ∞ обращается в прямую.

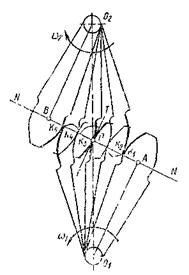
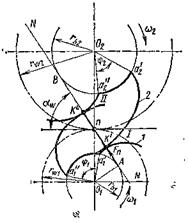
Взаимодействие эвольвент. Рассмотрим взаимодействие эвольвент двух окружностей радиуса r_b1 и r_b2 c центрами О₁ и О₂ (рис. 13.11), вокруг которых могут вращаться эвольвенты 1 и 2.

Пусть в положении I эвольвенты касаются в точке К΄. В этой точке они имеют общую касательную и, следовательно, общую нормаль АВ. Эта нормаль является производящей прямой обеих эвольвент и поэтому касается обеих основных окружностей. Из рассмотренного вытекает очень важное свойство эвольвент: у двух сопряженных эвольвент радиусы кривизны точки касания лежат на общей нормали.

Повернем основную окружность с эвольвентой I на некоторый угол φ₁ вокруг центра О₁. При этом эвольвента I окажет давление на эвольвенту 2; это давление F_n может передаваться только по общей нормали к обеим кривым, т.е. по линии АВ. Следовательно, общая нормаль является и линией давления. Поскольку линия давления не проходит через центр О₂, то вторая основная окружность вместе с эвольвентой «повернется на некоторый угол φ₂. Таким образом, посредством двух эвольвентных профилей можно осуществить передачу движения.

В новом положении II эвольвенты соприкасаются в точке К″, имея общую касательную и общую нормаль, касающуюся основных окружностей, т.е. нормаль АВ. Таким образом, общая нормаль АВ является геометрическим местом точек касания взаимодействующих эвольвент; ее называют линией зацепления. Из сказанного следует, что линия зацепления является линией давления.

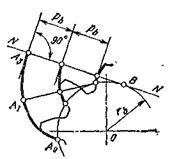
Острый угол между линией зацепления и перпендикуляром к межосевой линии называется углом зацепления α_ω; его стандартное значение для эвольвентных зацеплений α_ω = 20⁰.

Точка пересечения нормали АВ и линии межосевого расстояния является полюсом зацепления П. Поскольку при вращении эвольвент положение О₁ и О₂ не изменяется, то не меняется и положение полюса; тем самым удовлетворено требование основной теоремы зацепления.

При повороте эвольвент соответствующие дуги основных окружностей а₁΄а₁″ и а₂΄а₂″ равны между собой, поскольку каждая из них равна расстоянию К΄К″ по общей нормали, т.е. а₁΄а₁″ = К΄К″ = а₂΄а₂″, а значит, r_b1 φ₁ = r_b2 φ₂. Так как угловые скорости пропорциональны углам поворота, то

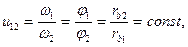
т.е. отношение угловых скоростей двух взаимодействующих эвольвентных профилей обратно пропорционально радиусам их основных окружностей и не зависит от межосевого расстояния этих окружностей.

Проведем из центров О₁ и О₂ окружности, касающиеся в полюсе зацепления и связанные с эвольвентными дугами 1 и 2; эти окружности называются начальными окружностями. Радиусы начальных окружностей r_ω1 = O₁П и r_ω2 = О₂П меняются при изменении расстояния О₁О₂. Из подобия треугольников О₁ПА и О₂ПВ имеем

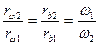и .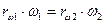

В таком случае скорости точек начальных окружностей v₁ = r₁ · ω₁ и v₂ = r₂ · ω₂ равны между собой, т.е. начальные окружности перекатываются без скольжения. Так как эвольвентные профили взаимодействуют различными участками (считая от основания эвольвенты), т.е. дугами различной длины, то их относительное движение происходит со скольжением: чем дальше от полюса, тем больше разница в соответствующих дугах и больше скольжение, наибольшее скольжение имеет место у основания эвольвенты. В полюсе скольжения нет; при переходе через полюс изменяется направление скольжения.

Взаимодействие эвольвентных профилей сопровождается трением. Сила трения достигает наибольшего значения вблизи полюса, где скорость скольжения наименьшая.

Перечень вопросов для контроля знаний:

1. Укажите формулировку основной теоремы зацепления.

2. Какая прямая называется межосевой линией колес?

3. Где располагается полюс зацепления?

4. Какая линия называется линией зацепления?

5. Какие окружности называются начальными окружностями?

6. Что позволяет определить основной закон зацепления?

7. Какие кривые называются рулеттами?

8. Укажите преимущества эвольвентного зацепления.

9. Укажите основные свойства эвольвенты.

10. Какой угол называется углом зацепления?